Discovering Symbolic Differential Equations with Symmetry Invariants

Discovering symbolic differential equations from data uncovers fundamental dynamical laws underlying complex systems. However, existing methods often struggle with the vast search space of equations and may produce equations that violate known physical laws. In this work, we address these problems by introducing the concept of \textit{symmetry invariants} in equation discovery. We leverage the fact that differential equations admitting a symmetry group can be expressed in terms of differential invariants of symmetry transformations. Thus, we propose to use these invariants as atomic entities in equation discovery, ensuring the discovered equations satisfy the specified symmetry. Our approach integrates seamlessly with existing equation discovery methods such as sparse regression and genetic programming, improving their accuracy and efficiency. We validate the proposed method through applications to various physical systems, such as fluid and reaction-diffusion, demonstrating its ability to recover parsimonious and interpretable equations that respect the laws of physics.

AtlasD: Automatic Local Symmetry Discovery

Existing symmetry discovery methods predominantly focus on global transformations across the entire system or space, but they fail to consider the symmetries in local neighborhoods. This may result in the reported symmetry group being a misrepresentation of the true symmetry. In this paper, we formalize the notion of local symmetry as atlas equivariance. Our proposed pipeline, automatic local symmetry discovery (AtlasD), recovers the local symmetries of a function by training local predictor networks and then learning a Lie group basis to which the predictors are equivariant. We demonstrate AtlasD is capable of discovering local symmetry groups with multiple connected components in top-quark tagging and partial differential equation experiments. The discovered local symmetry is shown to be a useful inductive bias that improves the performance of downstream tasks in climate segmentation and vision tasks.

Symmetry-Informed Governing Equation Discovery

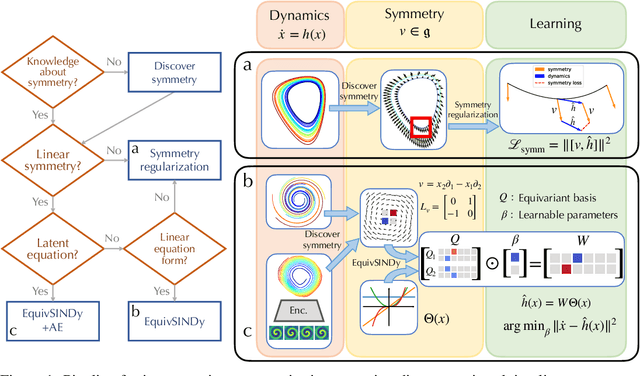
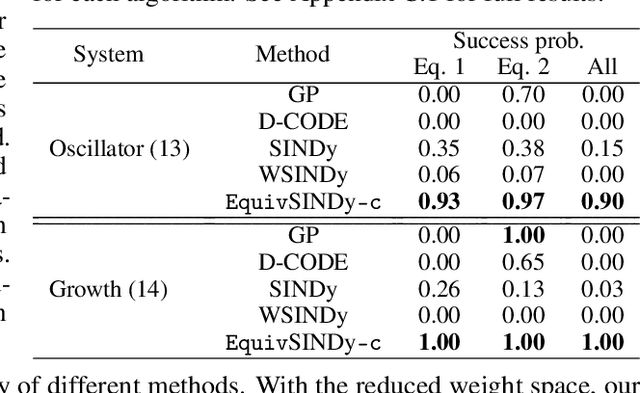
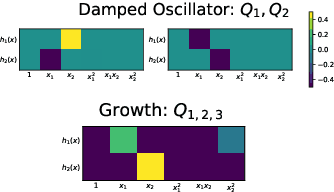
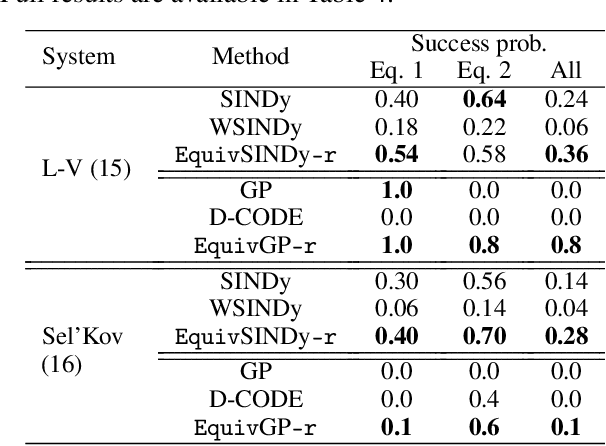
Despite the advancements in learning governing differential equations from observations of dynamical systems, data-driven methods are often unaware of fundamental physical laws, such as frame invariance. As a result, these algorithms may search an unnecessarily large space and discover equations that are less accurate or overly complex. In this paper, we propose to leverage symmetry in automated equation discovery to compress the equation search space and improve the accuracy and simplicity of the learned equations. Specifically, we derive equivariance constraints from the time-independent symmetries of ODEs. Depending on the types of symmetries, we develop a pipeline for incorporating symmetry constraints into various equation discovery algorithms, including sparse regression and genetic programming. In experiments across a diverse range of dynamical systems, our approach demonstrates better robustness against noise and recovers governing equations with significantly higher probability than baselines without symmetry.

Latent Space Symmetry Discovery

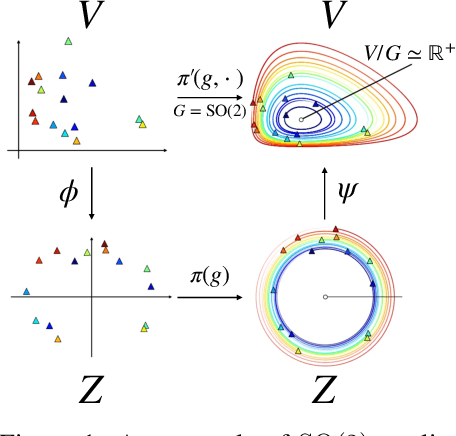
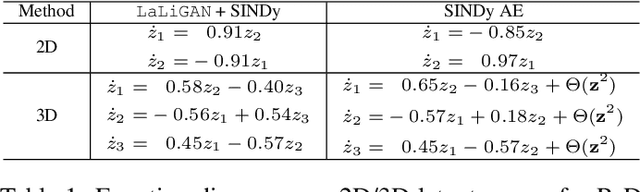
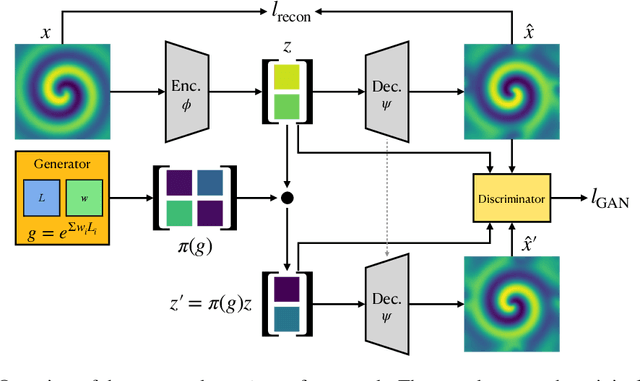
Equivariant neural networks require explicit knowledge of the symmetry group. Automatic symmetry discovery methods aim to relax this constraint and learn invariance and equivariance from data. However, existing symmetry discovery methods are limited to linear symmetries in their search space and cannot handle the complexity of symmetries in real-world, often high-dimensional data. We propose a novel generative model, Latent LieGAN (LaLiGAN), which can discover nonlinear symmetries from data. It learns a mapping from data to a latent space where the symmetries become linear and simultaneously discovers symmetries in the latent space. Theoretically, we show that our method can express any nonlinear symmetry under certain conditions. Experimentally, our method can capture the intrinsic symmetry in high-dimensional observations, which results in a well-structured latent space that is useful for other downstream tasks. We demonstrate the use cases for LaLiGAN in improving equation discovery and long-term forecasting for various dynamical systems.

Generative Adversarial Symmetry Discovery

Despite the success of equivariant neural networks in scientific applications, they require knowing the symmetry group a priori. However, it may be difficult to know the right symmetry to use as an inductive bias in practice and enforcing the wrong symmetry could hurt the performance. In this paper, we propose a framework, LieGAN, to automatically discover equivariances from a dataset using a paradigm akin to generative adversarial training. Specifically, a generator learns a group of transformations applied to the data, which preserves the original distribution and fools the discriminator. LieGAN represents symmetry as interpretable Lie algebra basis and can discover various symmetries such as rotation group $\mathrm{SO}(n)$ and restricted Lorentz group $\mathrm{SO}(1,3)^+$ in trajectory prediction and top quark tagging tasks. The learned symmetry can also be readily used in several existing equivariant neural networks to improve accuracy and generalization in prediction.