Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey

This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing fundamental concepts, traditional methods, and benchmark datasets, then examine the various roles ML plays in improving CFD. The literature systematically reviews papers in recent five years and introduces a novel classification for forward modeling: Data-driven Surrogates, Physics-Informed Surrogates, and ML-assisted Numerical Solutions. Furthermore, we also review the latest ML methods in inverse design and control, offering a novel classification and providing an in-depth discussion. Then we highlight real-world applications of ML for CFD in critical scientific and engineering disciplines, including aerodynamics, combustion, atmosphere & ocean science, biology fluid, plasma, symbolic regression, and reduced order modeling. Besides, we identify key challenges and advocate for future research directions to address these challenges, such as multi-scale representation, physical knowledge encoding, scientific foundation model and automatic scientific discovery. This review serves as a guide for the rapidly expanding ML for CFD community, aiming to inspire insights for future advancements. We draw the conclusion that ML is poised to significantly transform CFD research by enhancing simulation accuracy, reducing computational time, and enabling more complex analyses of fluid dynamics. The paper resources can be viewed at https://github.com/WillDreamer/Awesome-AI4CFD.

FMint: Bridging Human Designed and Data Pretrained Models for Differential Equation Foundation Model

Human-designed algorithms have long been fundamental in solving a variety of scientific and engineering challenges. Recently, data-driven deep learning methods have also risen to prominence, offering innovative solutions across numerous scientific fields. While traditional algorithms excel in capturing the core aspects of specific problems, they often lack the flexibility needed for varying problem conditions due to the absence of specific data. Conversely, while data-driven approaches utilize vast datasets, they frequently fall short in domain-specific knowledge. To bridge these gaps, we introduce \textbf{FMint} (Foundation Model based on Initialization), a generative pre-trained model that synergizes the precision of human-designed algorithms with the adaptability of data-driven methods. This model is specifically engineered for high-accuracy simulation of dynamical systems. Starting from initial trajectories provided by conventional methods, FMint quickly delivers highly accurate solutions. It incorporates in-context learning and has been pre-trained on a diverse corpus of 500,000 dynamical systems, showcasing exceptional generalization across a broad spectrum of real-world applications. By effectively combining algorithmic rigor with data-driven flexibility, FMint sets the stage for the next generation of scientific foundation models, tackling complex problems with both efficiency and high accuracy.

A Finite Expression Method for Solving High-Dimensional Committor Problems

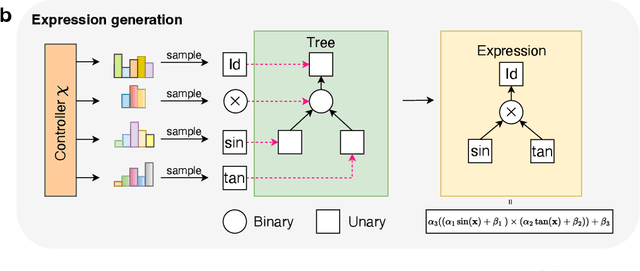
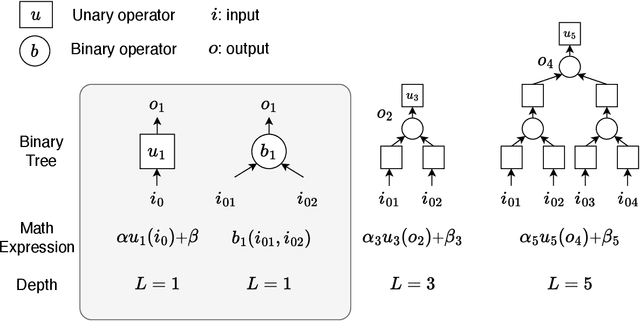
Transition path theory (TPT) is a mathematical framework for quantifying rare transition events between a pair of selected metastable states $A$ and $B$. Central to TPT is the committor function, which describes the probability to hit the metastable state $B$ prior to $A$ from any given starting point of the phase space. Once the committor is computed, the transition channels and the transition rate can be readily found. The committor is the solution to the backward Kolmogorov equation with appropriate boundary conditions. However, solving it is a challenging task in high dimensions due to the need to mesh a whole region of the ambient space. In this work, we explore the finite expression method (FEX, Liang and Yang (2022)) as a tool for computing the committor. FEX approximates the committor by an algebraic expression involving a fixed finite number of nonlinear functions and binary arithmetic operations. The optimal nonlinear functions, the binary operations, and the numerical coefficients in the expression template are found via reinforcement learning. The FEX-based committor solver is tested on several high-dimensional benchmark problems. It gives comparable or better results than neural network-based solvers. Most importantly, FEX is capable of correctly identifying the algebraic structure of the solution which allows one to reduce the committor problem to a low-dimensional one and find the committor with any desired accuracy.