From Uncertain to Safe: Conformal Fine-Tuning of Diffusion Models for Safe PDE Control

The application of deep learning for partial differential equation (PDE)-constrained control is gaining increasing attention. However, existing methods rarely consider safety requirements crucial in real-world applications. To address this limitation, we propose Safe Diffusion Models for PDE Control (SafeDiffCon), which introduce the uncertainty quantile as model uncertainty quantification to achieve optimal control under safety constraints through both post-training and inference phases. Firstly, our approach post-trains a pre-trained diffusion model to generate control sequences that better satisfy safety constraints while achieving improved control objectives via a reweighted diffusion loss, which incorporates the uncertainty quantile estimated using conformal prediction. Secondly, during inference, the diffusion model dynamically adjusts both its generation process and parameters through iterative guidance and fine-tuning, conditioned on control targets while simultaneously integrating the estimated uncertainty quantile. We evaluate SafeDiffCon on three control tasks: 1D Burgers' equation, 2D incompressible fluid, and controlled nuclear fusion problem. Results demonstrate that SafeDiffCon is the only method that satisfies all safety constraints, whereas other classical and deep learning baselines fail. Furthermore, while adhering to safety constraints, SafeDiffCon achieves the best control performance.

On the Guidance of Flow Matching

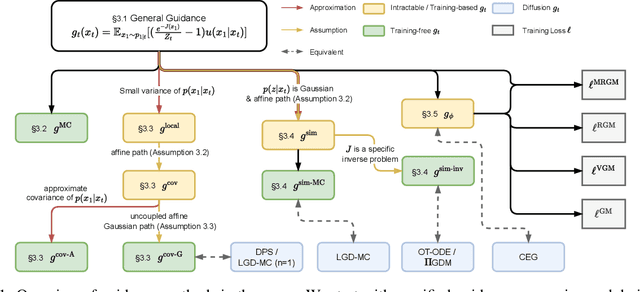
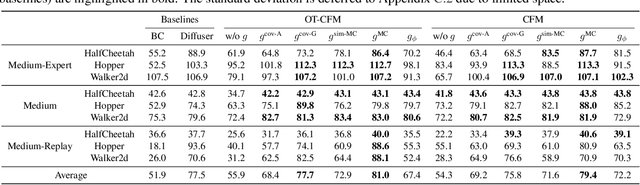
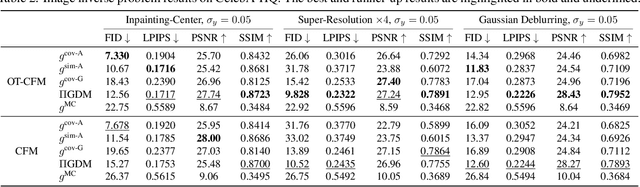
Flow matching has shown state-of-the-art performance in various generative tasks, ranging from image generation to decision-making, where guided generation is pivotal. However, the guidance of flow matching is more general than and thus substantially different from that of its predecessor, diffusion models. Therefore, the challenge in guidance for general flow matching remains largely underexplored. In this paper, we propose the first framework of general guidance for flow matching. From this framework, we derive a family of guidance techniques that can be applied to general flow matching. These include a new training-free asymptotically exact guidance, novel training losses for training-based guidance, and two classes of approximate guidance that cover classical gradient guidance methods as special cases. We theoretically investigate these different methods to give a practical guideline for choosing suitable methods in different scenarios. Experiments on synthetic datasets, image inverse problems, and offline reinforcement learning demonstrate the effectiveness of our proposed guidance methods and verify the correctness of our flow matching guidance framework. Code to reproduce the experiments can be found at https://github.com/AI4Science-WestlakeU/flow_guidance.

Wavelet Diffusion Neural Operator

Simulating and controlling physical systems described by partial differential equations (PDEs) are crucial tasks across science and engineering. Recently, diffusion generative models have emerged as a competitive class of methods for these tasks due to their ability to capture long-term dependencies and model high-dimensional states. However, diffusion models typically struggle with handling system states with abrupt changes and generalizing to higher resolutions. In this work, we propose Wavelet Diffusion Neural Operator (WDNO), a novel PDE simulation and control framework that enhances the handling of these complexities. WDNO comprises two key innovations. Firstly, WDNO performs diffusion-based generative modeling in the wavelet domain for the entire trajectory to handle abrupt changes and long-term dependencies effectively. Secondly, to address the issue of poor generalization across different resolutions, which is one of the fundamental tasks in modeling physical systems, we introduce multi-resolution training. We validate WDNO on five physical systems, including 1D advection equation, three challenging physical systems with abrupt changes (1D Burgers' equation, 1D compressible Navier-Stokes equation and 2D incompressible fluid), and a real-world dataset ERA5, which demonstrates superior performance on both simulation and control tasks over state-of-the-art methods, with significant improvements in long-term and detail prediction accuracy. Remarkably, in the challenging context of the 2D high-dimensional and indirect control task aimed at reducing smoke leakage, WDNO reduces the leakage by 33.2% compared to the second-best baseline.

Multimodal Policies with Physics-informed Representations

In the control problems of the PDE systems, observation is important to make the decision. However, the observation is generally sparse and missing in practice due to the limitation and fault of sensors. The above challenges cause observations with uncertain quantities and modalities. Therefore, how to leverage the uncertain observations as the states in control problems of the PDE systems has become a scientific problem. The dynamics of PDE systems rely on the initial conditions, boundary conditions, and PDE formula. Given the above three elements, PINNs can be used to solve the PDE systems. In this work, we discover that the neural network can also be used to identify and represent the PDE systems using PDE loss and sparse data loss. Inspired by the above discovery, we propose a Physics-Informed Representation (PIR) algorithm for multimodal policies in PDE systems' control. It leverages PDE loss to fit the neural network and data loss calculated on the observations with random quantities and modalities to propagate the information of initial conditions and boundary conditions into the inputs. The inputs can be the learnable parameters or the output of the encoders. Then, under the environments of the PDE systems, such inputs are the representation of the current state. In our experiments, the PIR illustrates the superior consistency with the features of the ground truth compared with baselines, even when there are missing modalities. Furthermore, PIR has been successfully applied in the downstream control tasks where the robot leverages the learned state by PIR faster and more accurately, passing through the complex vortex street from a random starting location to reach a random target.

Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey

This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing fundamental concepts, traditional methods, and benchmark datasets, then examine the various roles ML plays in improving CFD. The literature systematically reviews papers in recent five years and introduces a novel classification for forward modeling: Data-driven Surrogates, Physics-Informed Surrogates, and ML-assisted Numerical Solutions. Furthermore, we also review the latest ML methods in inverse design and control, offering a novel classification and providing an in-depth discussion. Then we highlight real-world applications of ML for CFD in critical scientific and engineering disciplines, including aerodynamics, combustion, atmosphere & ocean science, biology fluid, plasma, symbolic regression, and reduced order modeling. Besides, we identify key challenges and advocate for future research directions to address these challenges, such as multi-scale representation, physical knowledge encoding, scientific foundation model and automatic scientific discovery. This review serves as a guide for the rapidly expanding ML for CFD community, aiming to inspire insights for future advancements. We draw the conclusion that ML is poised to significantly transform CFD research by enhancing simulation accuracy, reducing computational time, and enabling more complex analyses of fluid dynamics. The paper resources can be viewed at https://github.com/WillDreamer/Awesome-AI4CFD.

Closed-loop Diffusion Control of Complex Physical Systems

The control problems of complex physical systems have wide applications in science and engineering. Several previous works have demonstrated that generative control methods based on diffusion models have significant advantages for solving these problems. However, existing generative control methods face challenges in handling closed-loop control, which is an inherent constraint for effective control of complex physical systems. In this paper, we propose a Closed-Loop Diffusion method for Physical systems Control (CL-DiffPhyCon). By adopting an asynchronous denoising schedule for different time steps, CL-DiffPhyCon generates control signals conditioned on real-time feedback from the environment. Thus, CL-DiffPhyCon is able to speed up diffusion control methods in a closed-loop framework. We evaluate CL-DiffPhyCon on the 1D Burgers' equation control and 2D incompressible fluid control tasks. The results demonstrate that CL-DiffPhyCon achieves notable control performance with significant sampling acceleration.

A Generative Approach to Control Complex Physical Systems

Controlling the evolution of complex physical systems is a fundamental task across science and engineering. Classical techniques suffer from limited applicability or huge computational costs. On the other hand, recent deep learning and reinforcement learning-based approaches often struggle to optimize long-term control sequences under the constraints of system dynamics. In this work, we introduce Diffusion Physical systems Control (DiffPhyCon), a new class of method to address the physical systems control problem. DiffPhyCon excels by simultaneously minimizing both the learned generative energy function and the predefined control objectives across the entire trajectory and control sequence. Thus, it can explore globally and identify near-optimal control sequences. Moreover, we enhance DiffPhyCon with prior reweighting, enabling the discovery of control sequences that significantly deviate from the training distribution. We test our method in 1D Burgers' equation and 2D jellyfish movement control in a fluid environment. Our method outperforms widely applied classical approaches and state-of-the-art deep learning and reinforcement learning methods. Notably, DiffPhyCon unveils an intriguing fast-close-slow-open pattern observed in the jellyfish, aligning with established findings in the field of fluid dynamics.

Better Neural PDE Solvers Through Data-Free Mesh Movers

Recently, neural networks have been extensively employed to solve partial differential equations (PDEs) in physical system modeling. While major studies focus on learning system evolution on predefined static mesh discretizations, some methods utilize reinforcement learning or supervised learning techniques to create adaptive and dynamic meshes, due to the dynamic nature of these systems. However, these approaches face two primary challenges: (1) the need for expensive optimal mesh data, and (2) the change of the solution space's degree of freedom and topology during mesh refinement. To address these challenges, this paper proposes a neural PDE solver with a neural mesh adapter. To begin with, we introduce a novel data-free neural mesh adaptor, called Data-free Mesh Mover (DMM), with two main innovations. Firstly, it is an operator that maps the solution to adaptive meshes and is trained using the Monge-Ampere equation without optimal mesh data. Secondly, it dynamically changes the mesh by moving existing nodes rather than adding or deleting nodes and edges. Theoretical analysis shows that meshes generated by DMM have the lowest interpolation error bound. Based on DMM, to efficiently and accurately model dynamic systems, we develop a moving mesh based neural PDE solver (MM-PDE) that embeds the moving mesh with a two-branch architecture and a learnable interpolation framework to preserve information within the data. Empirical experiments demonstrate that our method generates suitable meshes and considerably enhances accuracy when modeling widely considered PDE systems.

Deep Random Vortex Method for Simulation and Inference of Navier-Stokes Equations

Navier-Stokes equations are significant partial differential equations that describe the motion of fluids such as liquids and air. Due to the importance of Navier-Stokes equations, the development on efficient numerical schemes is important for both science and engineer. Recently, with the development of AI techniques, several approaches have been designed to integrate deep neural networks in simulating and inferring the fluid dynamics governed by incompressible Navier-Stokes equations, which can accelerate the simulation or inferring process in a mesh-free and differentiable way. In this paper, we point out that the capability of existing deep Navier-Stokes informed methods is limited to handle non-smooth or fractional equations, which are two critical situations in reality. To this end, we propose the \emph{Deep Random Vortex Method} (DRVM), which combines the neural network with a random vortex dynamics system equivalent to the Navier-Stokes equation. Specifically, the random vortex dynamics motivates a Monte Carlo based loss function for training the neural network, which avoids the calculation of derivatives through auto-differentiation. Therefore, DRVM not only can efficiently solve Navier-Stokes equations involving rough path, non-differentiable initial conditions and fractional operators, but also inherits the mesh-free and differentiable benefits of the deep-learning-based solver. We conduct experiments on the Cauchy problem, parametric solver learning, and the inverse problem of both 2-d and 3-d incompressible Navier-Stokes equations. The proposed method achieves accurate results for simulation and inference of Navier-Stokes equations. Especially for the cases that include singular initial conditions, DRVM significantly outperforms existing PINN method.

Neural Operator with Regularity Structure for Modeling Dynamics Driven by SPDEs

Stochastic partial differential equations (SPDEs) are significant tools for modeling dynamics in many areas including atmospheric sciences and physics. Neural Operators, generations of neural networks with capability of learning maps between infinite-dimensional spaces, are strong tools for solving parametric PDEs. However, they lack the ability to modeling SPDEs which usually have poor regularity due to the driving noise. As the theory of regularity structure has achieved great successes in analyzing SPDEs and provides the concept model feature vectors that well-approximate SPDEs' solutions, we propose the Neural Operator with Regularity Structure (NORS) which incorporates the feature vectors for modeling dynamics driven by SPDEs. We conduct experiments on various of SPDEs including the dynamic Phi41 model and the 2d stochastic Navier-Stokes equation, and the results demonstrate that the NORS is resolution-invariant, efficient, and achieves one order of magnitude lower error with a modest amount of data.