Neural Implicit Solution Formula for Efficiently Solving Hamilton-Jacobi Equations

This paper presents an implicit solution formula for the Hamilton-Jacobi partial differential equation (HJ PDE). The formula is derived using the method of characteristics and is shown to coincide with the Hopf and Lax formulas in the case where either the Hamiltonian or the initial function is convex. It provides a simple and efficient numerical approach for computing the viscosity solution of HJ PDEs, bypassing the need for the Legendre transform of the Hamiltonian or the initial condition, and the explicit computation of individual characteristic trajectories. A deep learning-based methodology is proposed to learn this implicit solution formula, leveraging the mesh-free nature of deep learning to ensure scalability for high-dimensional problems. Building upon this framework, an algorithm is developed that approximates the characteristic curves piecewise linearly for state-dependent Hamiltonians. Extensive experimental results demonstrate that the proposed method delivers highly accurate solutions, even for nonconvex Hamiltonians, and exhibits remarkable scalability, achieving computational efficiency for problems up to 40 dimensions.

OT-Transformer: A Continuous-time Transformer Architecture with Optimal Transport Regularization

Transformers have achieved state-of-the-art performance in numerous tasks. In this paper, we propose a continuous-time formulation of transformers. Specifically, we consider a dynamical system whose governing equation is parametrized by transformer blocks. We leverage optimal transport theory to regularize the training problem, which enhances stability in training and improves generalization of the resulting model. Moreover, we demonstrate in theory that this regularization is necessary as it promotes uniqueness and regularity of solutions. Our model is flexible in that almost any existing transformer architectures can be adopted to construct the dynamical system with only slight modifications to the existing code. We perform extensive numerical experiments on tasks motivated by natural language processing, image classification, and point cloud classification. Our experimental results show that the proposed method improves the performance of its discrete counterpart and outperforms relevant comparing models.

In-Context Operator Learning for Linear Propagator Models

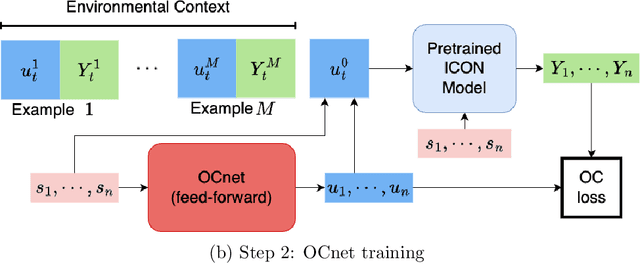
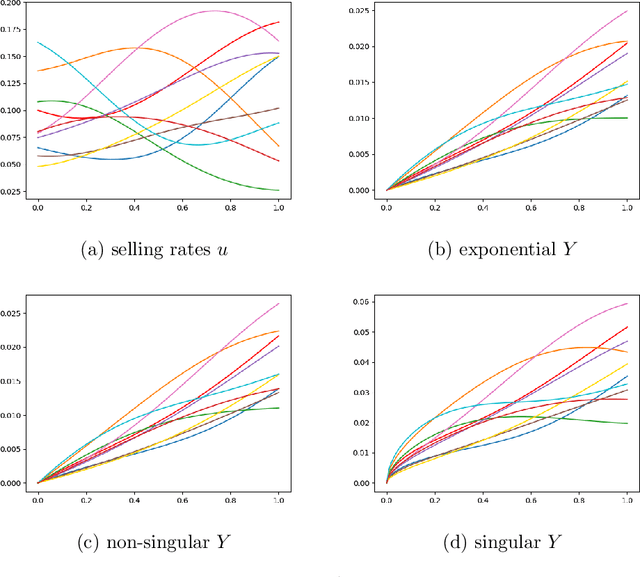
We study operator learning in the context of linear propagator models for optimal order execution problems with transient price impact \`a la Bouchaud et al. (2004) and Gatheral (2010). Transient price impact persists and decays over time according to some propagator kernel. Specifically, we propose to use In-Context Operator Networks (ICON), a novel transformer-based neural network architecture introduced by Yang et al. (2023), which facilitates data-driven learning of operators by merging offline pre-training with an online few-shot prompting inference. First, we train ICON to learn the operator from various propagator models that maps the trading rate to the induced transient price impact. The inference step is then based on in-context prediction, where ICON is presented only with a few examples. We illustrate that ICON is capable of accurately inferring the underlying price impact model from the data prompts, even with propagator kernels not seen in the training data. In a second step, we employ the pre-trained ICON model provided with context as a surrogate operator in solving an optimal order execution problem via a neural network control policy, and demonstrate that the exact optimal execution strategies from Abi Jaber and Neuman (2022) for the models generating the context are correctly retrieved. Our introduced methodology is very general, offering a new approach to solving optimal stochastic control problems with unknown state dynamics, inferred data-efficiently from a limited number of examples by leveraging the few-shot and transfer learning capabilities of transformer networks.

VICON: Vision In-Context Operator Networks for Multi-Physics Fluid Dynamics Prediction

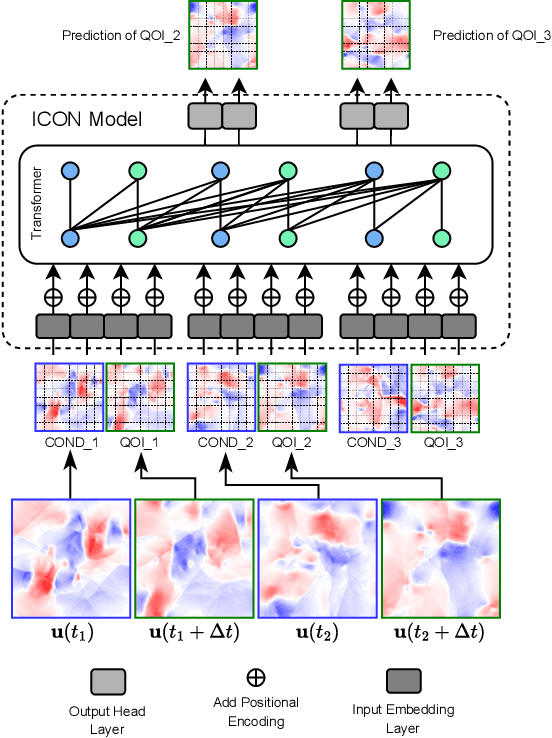
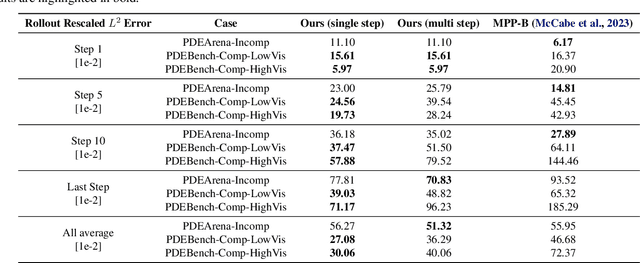
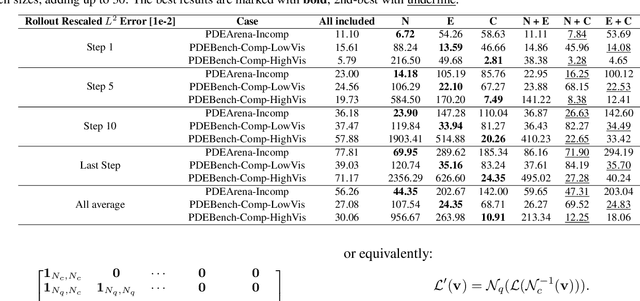
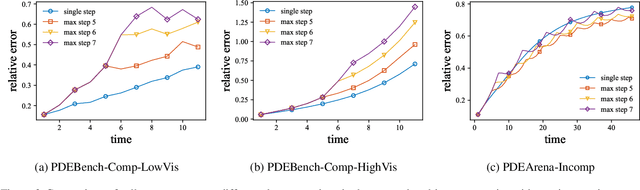
In-Context Operator Networks (ICONs) are models that learn operators across different types of PDEs using a few-shot, in-context approach. Although they show successful generalization to various PDEs, existing methods treat each data point as a single token, and suffer from computational inefficiency when processing dense data, limiting their application in higher spatial dimensions. In this work, we propose Vision In-Context Operator Networks (VICON), incorporating a vision transformer architecture that efficiently processes 2D functions through patch-wise operations. We evaluated our method on three fluid dynamics datasets, demonstrating both superior performance (reducing scaled $L^2$ error by $40\%$ and $61.6\%$ for two benchmark datasets for compressible flows, respectively) and computational efficiency (requiring only one-third of the inference time per frame) in long-term rollout predictions compared to the current state-of-the-art sequence-to-sequence model with fixed timestep prediction: Multiple Physics Pretraining (MPP). Compared to MPP, our method preserves the benefits of in-context operator learning, enabling flexible context formation when dealing with insufficient frame counts or varying timestep values.

A Natural Primal-Dual Hybrid Gradient Method for Adversarial Neural Network Training on Solving Partial Differential Equations

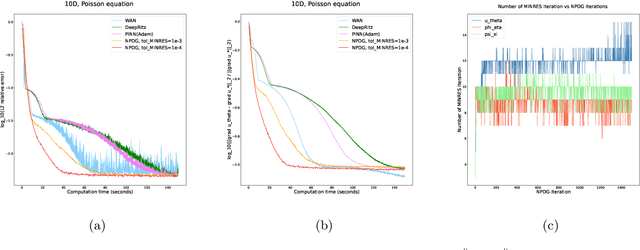
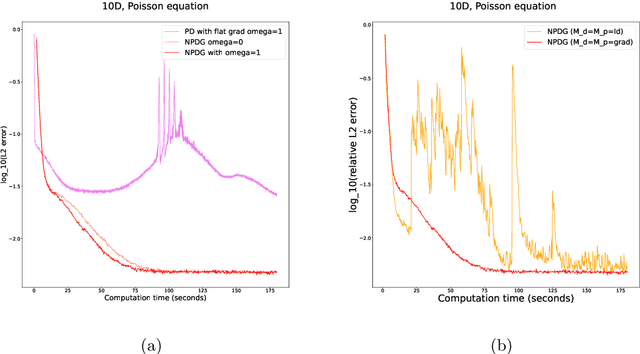
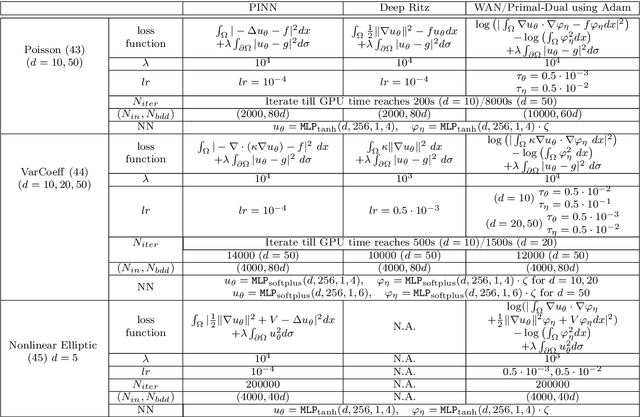
We propose a scalable preconditioned primal-dual hybrid gradient algorithm for solving partial differential equations (PDEs). We multiply the PDE with a dual test function to obtain an inf-sup problem whose loss functional involves lower-order differential operators. The Primal-Dual Hybrid Gradient (PDHG) algorithm is then leveraged for this saddle point problem. By introducing suitable precondition operators to the proximal steps in the PDHG algorithm, we obtain an alternative natural gradient ascent-descent optimization scheme for updating the neural network parameters. We apply the Krylov subspace method (MINRES) to evaluate the natural gradients efficiently. Such treatment readily handles the inversion of precondition matrices via matrix-vector multiplication. A posterior convergence analysis is established for the time-continuous version of the proposed method. The algorithm is tested on various types of PDEs with dimensions ranging from $1$ to $50$, including linear and nonlinear elliptic equations, reaction-diffusion equations, and Monge-Amp\`ere equations stemming from the $L^2$ optimal transport problems. We compare the performance of the proposed method with several commonly used deep learning algorithms such as physics-informed neural networks (PINNs), the DeepRitz method, weak adversarial networks (WANs), etc, for solving PDEs using the Adam and L-BFGS optimizers. The numerical results suggest that the proposed method performs efficiently and robustly and converges more stably.

Fried deconvolution

In this paper we present a new approach to deblur the effect of atmospheric turbulence in the case of long range imaging. Our method is based on an analytical formulation, the Fried kernel, of the atmosphere modulation transfer function (MTF) and a framelet based deconvolution algorithm. An important parameter is the refractive index structure which requires specific measurements to be known. Then we propose a method which provides a good estimation of this parameter from the input blurred image. The final algorithms are very easy to implement and show very good results on both simulated blur and real images.

2D Empirical Transforms. Wavelets, Ridgelets and Curvelets revisited

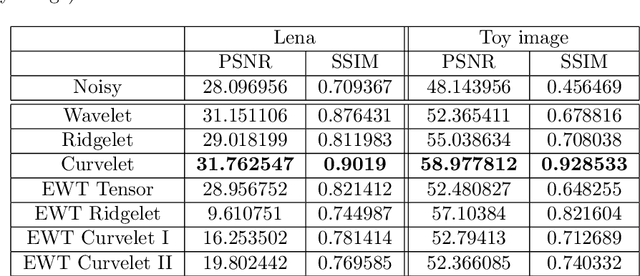
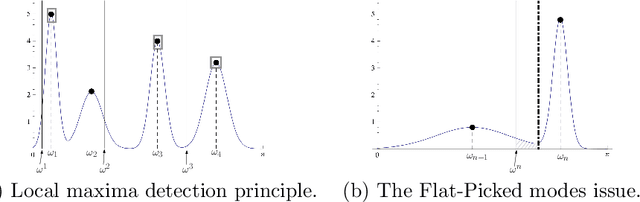
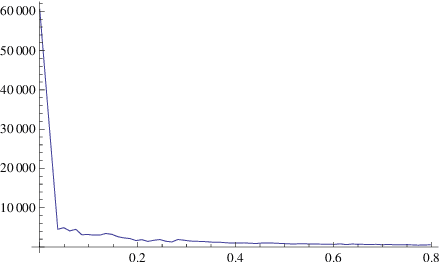
A recently developed new approach, called ``Empirical Wavelet Transform'', aims to build 1D adaptive wavelet frames accordingly to the analyzed signal. In this paper, we present several extensions of this approach to 2D signals (images). We revisit some well-known transforms (tensor wavelets, Littlewood-Paley wavelets, ridgelets and curvelets) and show that it is possible to build their empirical counterpart. We prove that such constructions lead to different adaptive frames which show some promising properties for image analysis and processing.

Wavelet Burst Accumulation for turbulence mitigation

In this paper, we investigate the extension of the recently proposed weighted Fourier burst accumulation (FBA) method into the wavelet domain. The purpose of FBA is to reconstruct a clean and sharp image from a sequence of blurred frames. This concept lies in the construction of weights to amplify dominant frequencies in the Fourier spectrum of each frame. The reconstructed image is then obtained by taking the inverse Fourier transform of the average of all processed spectra. In this paper, we first suggest to replace the rigid registration step used in the original algorithm by a non-rigid registration in order to be able to process sequences acquired through atmospheric turbulence. Second, we propose to work in a wavelet domain instead of the Fourier one. This leads us to the construction of two types of algorithms. Finally, we propose an alternative approach to replace the weighting idea by an approach promoting the sparsity in the used space. Several experiments are provided to illustrate the efficiency of the proposed methods.

Bregman implementation of Meyer's $G-$norm for cartoon + textures decomposition

In this paper, we design a very simple algorithm based on Split Bregman iterations to numerically solve the cartoon + textures decomposition model of Meyer. This results in a significant gain in speed compared to Chambolle's nonlinear projectors.

Score-based Neural Ordinary Differential Equations for Computing Mean Field Control Problems

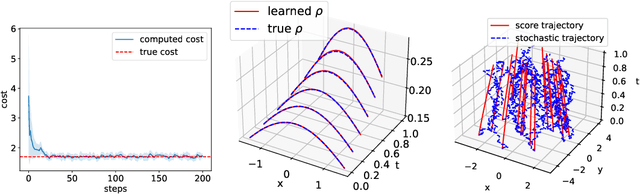
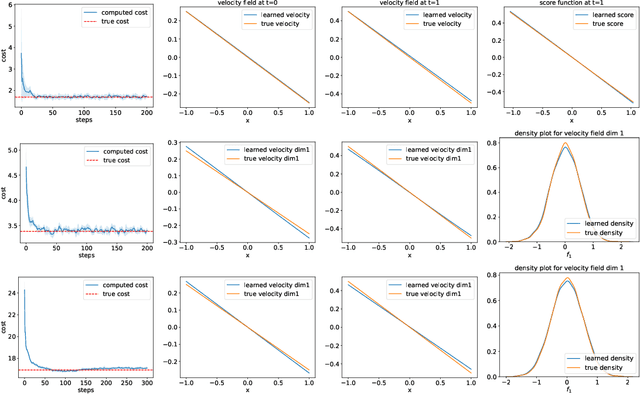
Classical neural ordinary differential equations (ODEs) are powerful tools for approximating the log-density functions in high-dimensional spaces along trajectories, where neural networks parameterize the velocity fields. This paper proposes a system of neural differential equations representing first- and second-order score functions along trajectories based on deep neural networks. We reformulate the mean field control (MFC) problem with individual noises into an unconstrained optimization problem framed by the proposed neural ODE system. Additionally, we introduce a novel regularization term to enforce characteristics of viscous Hamilton--Jacobi--Bellman (HJB) equations to be satisfied based on the evolution of the second-order score function. Examples include regularized Wasserstein proximal operators (RWPOs), probability flow matching of Fokker--Planck (FP) equations, and linear quadratic (LQ) MFC problems, which demonstrate the effectiveness and accuracy of the proposed method.