2D Empirical Transforms. Wavelets, Ridgelets and Curvelets revisited
Paper and Code
Oct 31, 2024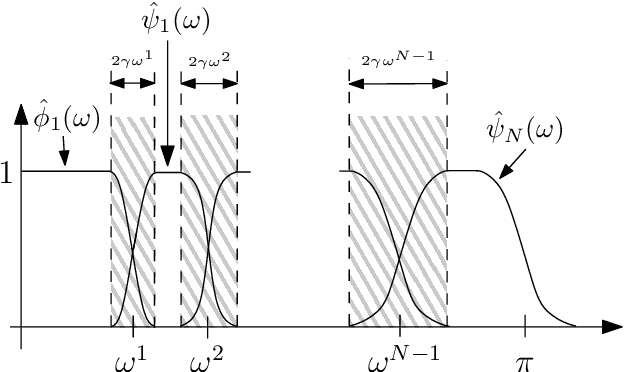
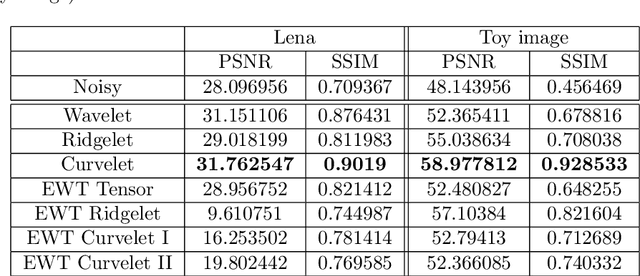
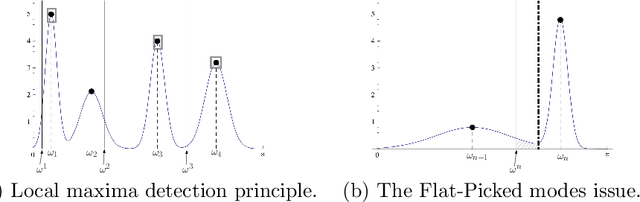
A recently developed new approach, called ``Empirical Wavelet Transform'', aims to build 1D adaptive wavelet frames accordingly to the analyzed signal. In this paper, we present several extensions of this approach to 2D signals (images). We revisit some well-known transforms (tensor wavelets, Littlewood-Paley wavelets, ridgelets and curvelets) and show that it is possible to build their empirical counterpart. We prove that such constructions lead to different adaptive frames which show some promising properties for image analysis and processing.
* SIAM Journal on Imaging Sciences, Vol.7, No.1, 157--186, January
2014
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge