2D Empirical Transforms. Wavelets, Ridgelets and Curvelets revisited

A recently developed new approach, called ``Empirical Wavelet Transform'', aims to build 1D adaptive wavelet frames accordingly to the analyzed signal. In this paper, we present several extensions of this approach to 2D signals (images). We revisit some well-known transforms (tensor wavelets, Littlewood-Paley wavelets, ridgelets and curvelets) and show that it is possible to build their empirical counterpart. We prove that such constructions lead to different adaptive frames which show some promising properties for image analysis and processing.

Fast Multipole Attention: A Divide-and-Conquer Attention Mechanism for Long Sequences

Transformer-based models have achieved state-of-the-art performance in many areas. However, the quadratic complexity of self-attention with respect to the input length hinders the applicability of Transformer-based models to long sequences. To address this, we present Fast Multipole Attention, a new attention mechanism that uses a divide-and-conquer strategy to reduce the time and memory complexity of attention for sequences of length $n$ from $\mathcal{O}(n^2)$ to $\mathcal{O}(n \log n)$ or $O(n)$, while retaining a global receptive field. The hierarchical approach groups queries, keys, and values into $\mathcal{O}( \log n)$ levels of resolution, where groups at greater distances are increasingly larger in size and the weights to compute group quantities are learned. As such, the interaction between tokens far from each other is considered in lower resolution in an efficient hierarchical manner. The overall complexity of Fast Multipole Attention is $\mathcal{O}(n)$ or $\mathcal{O}(n \log n)$, depending on whether the queries are down-sampled or not. This multi-level divide-and-conquer strategy is inspired by fast summation methods from $n$-body physics and the Fast Multipole Method. We perform evaluation on autoregressive and bidirectional language modeling tasks and compare our Fast Multipole Attention model with other efficient attention variants on medium-size datasets. We find empirically that the Fast Multipole Transformer performs much better than other efficient transformers in terms of memory size and accuracy. The Fast Multipole Attention mechanism has the potential to empower large language models with much greater sequence lengths, taking the full context into account in an efficient, naturally hierarchical manner during training and when generating long sequences.

Diffusion Random Feature Model

Diffusion probabilistic models have been successfully used to generate data from noise. However, most diffusion models are computationally expensive and difficult to interpret with a lack of theoretical justification. Random feature models on the other hand have gained popularity due to their interpretability but their application to complex machine learning tasks remains limited. In this work, we present a diffusion model-inspired deep random feature model that is interpretable and gives comparable numerical results to a fully connected neural network having the same number of trainable parameters. Specifically, we extend existing results for random features and derive generalization bounds between the distribution of sampled data and the true distribution using properties of score matching. We validate our findings by generating samples on the fashion MNIST dataset and instrumental audio data.

SPADE4: Sparsity and Delay Embedding based Forecasting of Epidemics

Predicting the evolution of diseases is challenging, especially when the data availability is scarce and incomplete. The most popular tools for modelling and predicting infectious disease epidemics are compartmental models. They stratify the population into compartments according to health status and model the dynamics of these compartments using dynamical systems. However, these predefined systems may not capture the true dynamics of the epidemic due to the complexity of the disease transmission and human interactions. In order to overcome this drawback, we propose Sparsity and Delay Embedding based Forecasting (SPADE4) for predicting epidemics. SPADE4 predicts the future trajectory of an observable variable without the knowledge of the other variables or the underlying system. We use random features model with sparse regression to handle the data scarcity issue and employ Takens' delay embedding theorem to capture the nature of the underlying system from the observed variable. We show that our approach outperforms compartmental models when applied to both simulated and real data.

SRMD: Sparse Random Mode Decomposition

Signal decomposition and multiscale signal analysis provide many useful tools for time-frequency analysis. We proposed a random feature method for analyzing time-series data by constructing a sparse approximation to the spectrogram. The randomization is both in the time window locations and the frequency sampling, which lowers the overall sampling and computational cost. The sparsification of the spectrogram leads to a sharp separation between time-frequency clusters which makes it easier to identify intrinsic modes, and thus leads to a new data-driven mode decomposition. The applications include signal representation, outlier removal, and mode decomposition. On the benchmark tests, we show that our approach outperforms other state-of-the-art decomposition methods.

HARFE: Hard-Ridge Random Feature Expansion

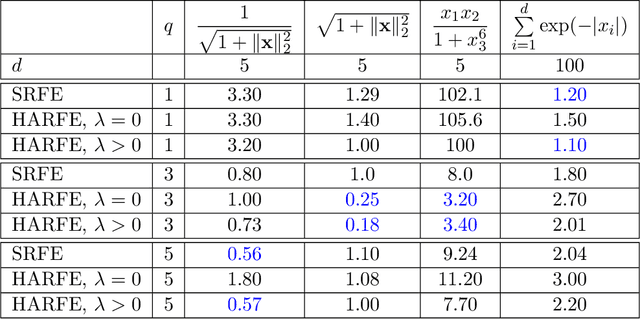
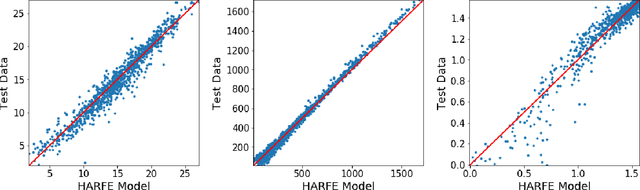
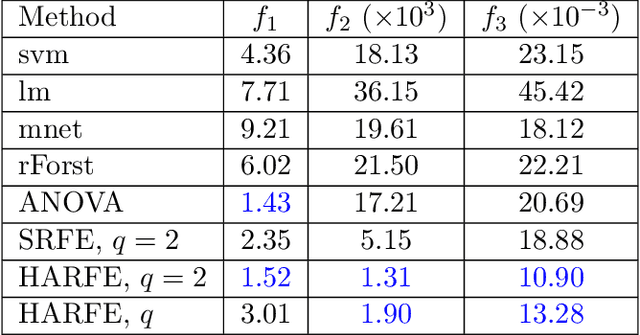
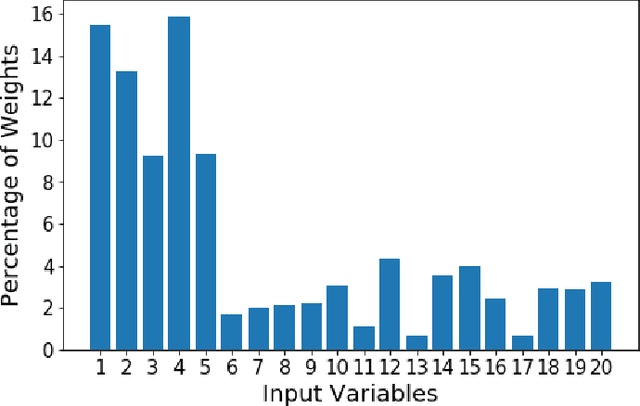
We propose a random feature model for approximating high-dimensional sparse additive functions called the hard-ridge random feature expansion method (HARFE). This method utilizes a hard-thresholding pursuit-based algorithm applied to the sparse ridge regression (SRR) problem to approximate the coefficients with respect to the random feature matrix. The SRR formulation balances between obtaining sparse models that use fewer terms in their representation and ridge-based smoothing that tend to be robust to noise and outliers. In addition, we use a random sparse connectivity pattern in the random feature matrix to match the additive function assumption. We prove that the HARFE method is guaranteed to converge with a given error bound depending on the noise and the parameters of the sparse ridge regression model. Based on numerical results on synthetic data as well as on real datasets, the HARFE approach obtains lower (or comparable) error than other state-of-the-art algorithms.

Adaptive Group Lasso Neural Network Models for Functions of Few Variables and Time-Dependent Data

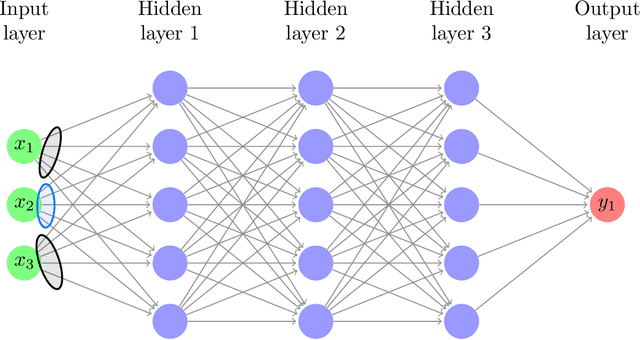
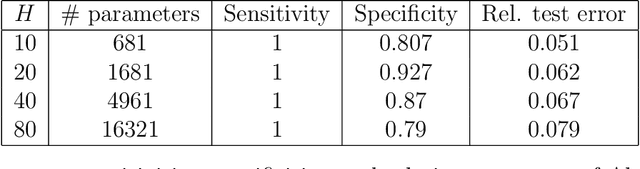
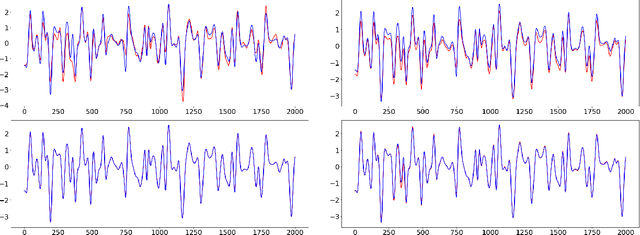
In this paper, we propose an adaptive group Lasso deep neural network for high-dimensional function approximation where input data are generated from a dynamical system and the target function depends on few active variables or few linear combinations of variables. We approximate the target function by a deep neural network and enforce an adaptive group Lasso constraint to the weights of a suitable hidden layer in order to represent the constraint on the target function. Our empirical studies show that the proposed method outperforms recent state-of-the-art methods including the sparse dictionary matrix method, neural networks with or without group Lasso penalty.

Function Approximation via Sparse Random Features

Random feature methods have been successful in various machine learning tasks, are easy to compute, and come with theoretical accuracy bounds. They serve as an alternative approach to standard neural networks since they can represent similar function spaces without a costly training phase. However, for accuracy, random feature methods require more measurements than trainable parameters, limiting their use for data-scarce applications or problems in scientific machine learning. This paper introduces the sparse random feature method that learns parsimonious random feature models utilizing techniques from compressive sensing. We provide uniform bounds on the approximation error for functions in a reproducing kernel Hilbert space depending on the number of samples and the distribution of features. The error bounds improve with additional structural conditions, such as coordinate sparsity, compact clusters of the spectrum, or rapid spectral decay. We show that the sparse random feature method outperforms shallow networks for well-structured functions and applications to scientific machine learning tasks.

Recovery guarantees for polynomial approximation from dependent data with outliers

Learning non-linear systems from noisy, limited, and/or dependent data is an important task across various scientific fields including statistics, engineering, computer science, mathematics, and many more. In general, this learning task is ill-posed; however, additional information about the data's structure or on the behavior of the unknown function can make the task well-posed. In this work, we study the problem of learning nonlinear functions from corrupted and dependent data. The learning problem is recast as a sparse robust linear regression problem where we incorporate both the unknown coefficients and the corruptions in a basis pursuit framework. The main contribution of our paper is to provide a reconstruction guarantee for the associated $\ell_1$-optimization problem where the sampling matrix is formed from dependent data. Specifically, we prove that the sampling matrix satisfies the null space property and the stable null space property, provided that the data is compact and satisfies a suitable concentration inequality. We show that our recovery results are applicable to various types of dependent data such as exponentially strongly $\alpha$-mixing data, geometrically $\mathcal{C}$-mixing data, and uniformly ergodic Markov chain. Our theoretical results are verified via several numerical simulations.