Yanming Kang
Fast Multipole Attention: A Divide-and-Conquer Attention Mechanism for Long Sequences
Oct 21, 2023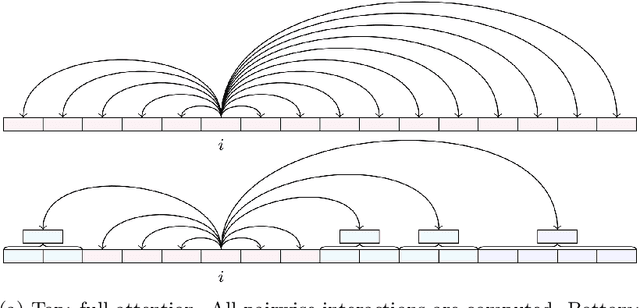
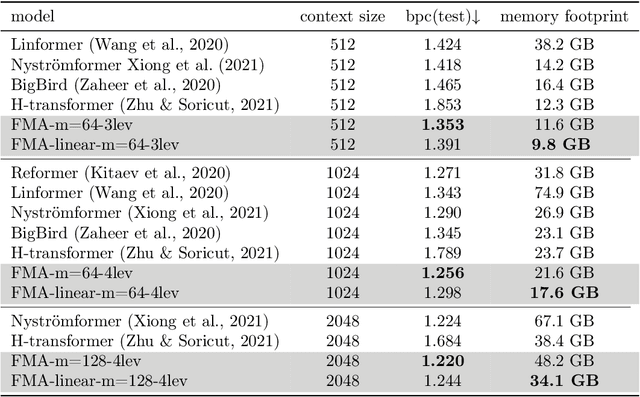
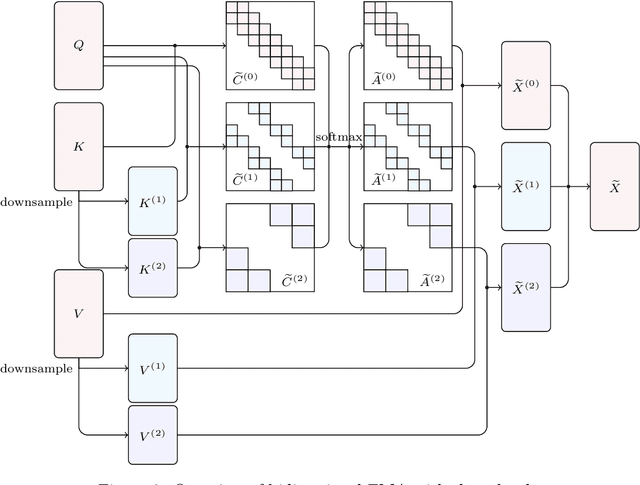
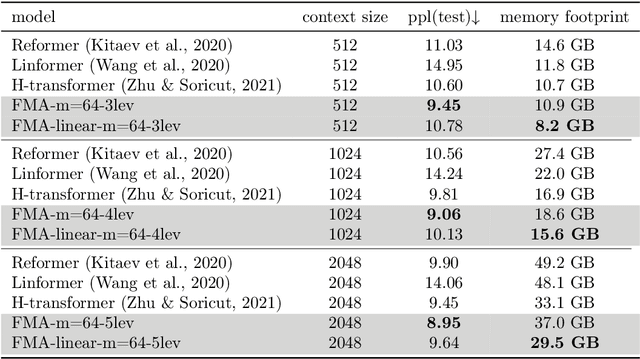
Abstract:Transformer-based models have achieved state-of-the-art performance in many areas. However, the quadratic complexity of self-attention with respect to the input length hinders the applicability of Transformer-based models to long sequences. To address this, we present Fast Multipole Attention, a new attention mechanism that uses a divide-and-conquer strategy to reduce the time and memory complexity of attention for sequences of length $n$ from $\mathcal{O}(n^2)$ to $\mathcal{O}(n \log n)$ or $O(n)$, while retaining a global receptive field. The hierarchical approach groups queries, keys, and values into $\mathcal{O}( \log n)$ levels of resolution, where groups at greater distances are increasingly larger in size and the weights to compute group quantities are learned. As such, the interaction between tokens far from each other is considered in lower resolution in an efficient hierarchical manner. The overall complexity of Fast Multipole Attention is $\mathcal{O}(n)$ or $\mathcal{O}(n \log n)$, depending on whether the queries are down-sampled or not. This multi-level divide-and-conquer strategy is inspired by fast summation methods from $n$-body physics and the Fast Multipole Method. We perform evaluation on autoregressive and bidirectional language modeling tasks and compare our Fast Multipole Attention model with other efficient attention variants on medium-size datasets. We find empirically that the Fast Multipole Transformer performs much better than other efficient transformers in terms of memory size and accuracy. The Fast Multipole Attention mechanism has the potential to empower large language models with much greater sequence lengths, taking the full context into account in an efficient, naturally hierarchical manner during training and when generating long sequences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge