Stochastic Reinforcement Learning with Stability Guarantees for Control of Unknown Nonlinear Systems

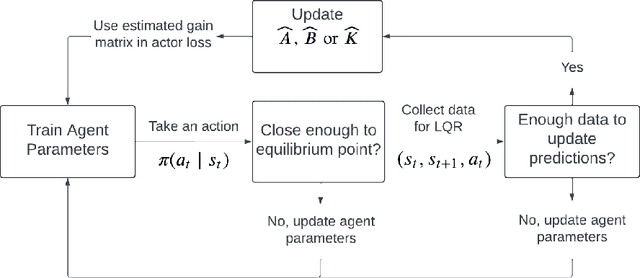
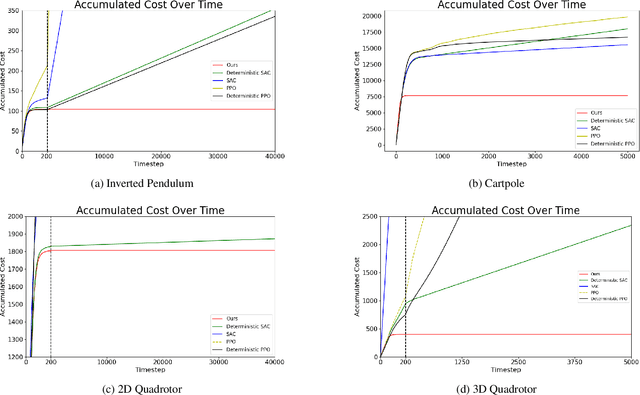
Designing a stabilizing controller for nonlinear systems is a challenging task, especially for high-dimensional problems with unknown dynamics. Traditional reinforcement learning algorithms applied to stabilization tasks tend to drive the system close to the equilibrium point. However, these approaches often fall short of achieving true stabilization and result in persistent oscillations around the equilibrium point. In this work, we propose a reinforcement learning algorithm that stabilizes the system by learning a local linear representation ofthe dynamics. The main component of the algorithm is integrating the learned gain matrix directly into the neural policy. We demonstrate the effectiveness of our algorithm on several challenging high-dimensional dynamical systems. In these simulations, our algorithm outperforms popular reinforcement learning algorithms, such as soft actor-critic (SAC) and proximal policy optimization (PPO), and successfully stabilizes the system. To support the numerical results, we provide a theoretical analysis of the feasibility of the learned algorithm for both deterministic and stochastic reinforcement learning settings, along with a convergence analysis of the proposed learning algorithm. Furthermore, we verify that the learned control policies indeed provide asymptotic stability for the nonlinear systems.

Sum-of-norms regularized Nonnegative Matrix Factorization

When applying nonnegative matrix factorization (NMF), generally the rank parameter is unknown. Such rank in NMF, called the nonnegative rank, is usually estimated heuristically since computing the exact value of it is NP-hard. In this work, we propose an approximation method to estimate such rank while solving NMF on-the-fly. We use sum-of-norm (SON), a group-lasso structure that encourages pairwise similarity, to reduce the rank of a factor matrix where the rank is overestimated at the beginning. On various datasets, SON-NMF is able to reveal the correct nonnegative rank of the data without any prior knowledge nor tuning. SON-NMF is a nonconvx nonsmmoth non-separable non-proximable problem, solving it is nontrivial. First, as rank estimation in NMF is NP-hard, the proposed approach does not enjoy a lower computational complexity. Using a graph-theoretic argument, we prove that the complexity of the SON-NMF is almost irreducible. Second, the per-iteration cost of any algorithm solving SON-NMF is possibly high, which motivated us to propose a first-order BCD algorithm to approximately solve SON-NMF with a low per-iteration cost, in which we do so by the proximal average operator. Lastly, we propose a simple greedy method for post-processing. SON-NMF exhibits favourable features for applications. Beside the ability to automatically estimate the rank from data, SON-NMF can deal with rank-deficient data matrix, can detect weak component with small energy. Furthermore, on the application of hyperspectral imaging, SON-NMF handle the issue of spectral variability naturally.

First-order PDES for Graph Neural Networks: Advection And Burgers Equation Models

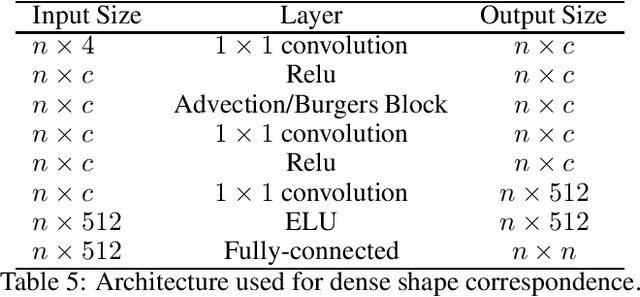
Graph Neural Networks (GNNs) have established themselves as the preferred methodology in a multitude of domains, ranging from computer vision to computational biology, especially in contexts where data inherently conform to graph structures. While many existing methods have endeavored to model GNNs using various techniques, a prevalent challenge they grapple with is the issue of over-smoothing. This paper presents new Graph Neural Network models that incorporate two first-order Partial Differential Equations (PDEs). These models do not increase complexity but effectively mitigate the over-smoothing problem. Our experimental findings highlight the capacity of our new PDE model to achieve comparable results with higher-order PDE models and fix the over-smoothing problem up to 64 layers. These results underscore the adaptability and versatility of GNNs, indicating that unconventional approaches can yield outcomes on par with established techniques.

Fast Multipole Attention: A Divide-and-Conquer Attention Mechanism for Long Sequences

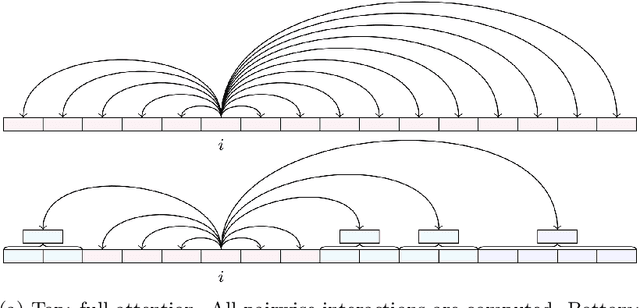
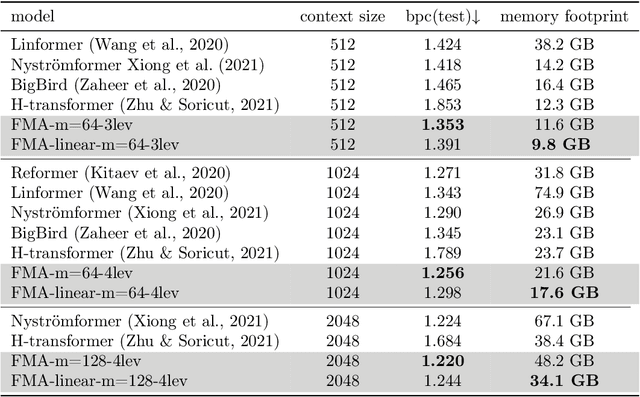
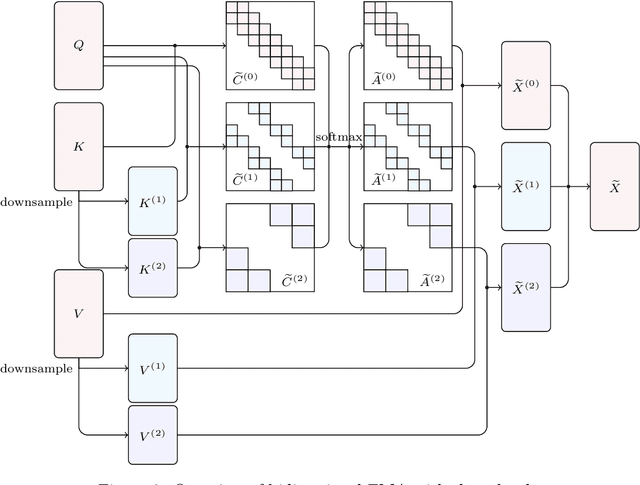
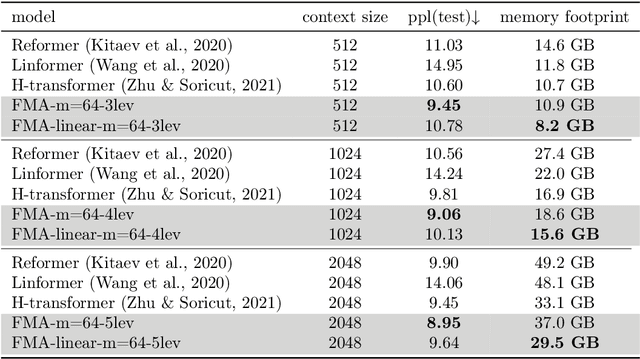
Transformer-based models have achieved state-of-the-art performance in many areas. However, the quadratic complexity of self-attention with respect to the input length hinders the applicability of Transformer-based models to long sequences. To address this, we present Fast Multipole Attention, a new attention mechanism that uses a divide-and-conquer strategy to reduce the time and memory complexity of attention for sequences of length $n$ from $\mathcal{O}(n^2)$ to $\mathcal{O}(n \log n)$ or $O(n)$, while retaining a global receptive field. The hierarchical approach groups queries, keys, and values into $\mathcal{O}( \log n)$ levels of resolution, where groups at greater distances are increasingly larger in size and the weights to compute group quantities are learned. As such, the interaction between tokens far from each other is considered in lower resolution in an efficient hierarchical manner. The overall complexity of Fast Multipole Attention is $\mathcal{O}(n)$ or $\mathcal{O}(n \log n)$, depending on whether the queries are down-sampled or not. This multi-level divide-and-conquer strategy is inspired by fast summation methods from $n$-body physics and the Fast Multipole Method. We perform evaluation on autoregressive and bidirectional language modeling tasks and compare our Fast Multipole Attention model with other efficient attention variants on medium-size datasets. We find empirically that the Fast Multipole Transformer performs much better than other efficient transformers in terms of memory size and accuracy. The Fast Multipole Attention mechanism has the potential to empower large language models with much greater sequence lengths, taking the full context into account in an efficient, naturally hierarchical manner during training and when generating long sequences.

Downlink Compression Improves TopK Sparsification

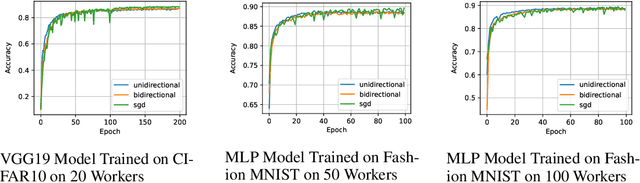
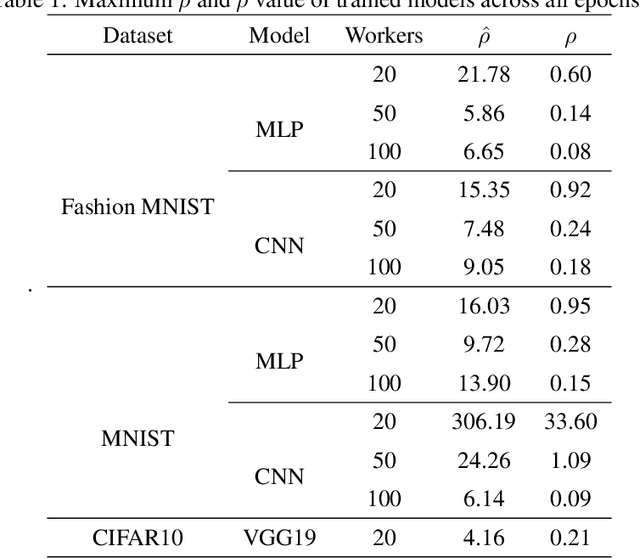
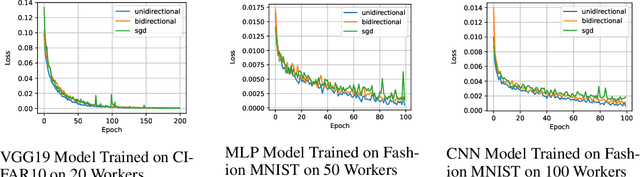
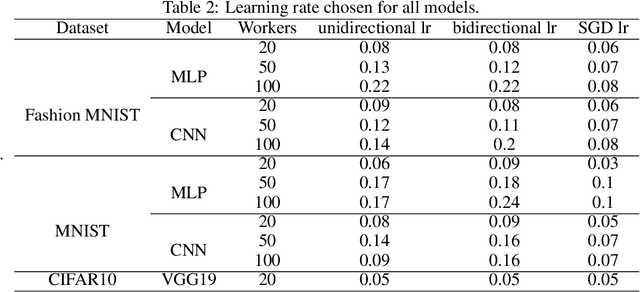
Training large neural networks is time consuming. To speed up the process, distributed training is often used. One of the largest bottlenecks in distributed training is communicating gradients across different nodes. Different gradient compression techniques have been proposed to alleviate the communication bottleneck, including topK gradient sparsification, which truncates the gradient to the largest K components before sending it to other nodes. While some authors have investigated topK gradient sparsification in the parameter-server framework by applying topK compression in both the worker-to-server (uplink) and server-to-worker (downlink) direction, the currently accepted belief says that adding extra compression degrades the convergence of the model. We demonstrate, on the contrary, that adding downlink compression can potentially improve the performance of topK sparsification: not only does it reduce the amount of communication per step, but also, counter-intuitively, can improve the upper bound in the convergence analysis. To show this, we revisit non-convex convergence analysis of topK stochastic gradient descent (SGD) and extend it from the unidirectional to the bidirectional setting. We also remove a restriction of the previous analysis that requires unrealistically large values of K. We experimentally evaluate bidirectional topK SGD against unidirectional topK SGD and show that models trained with bidirectional topK SGD will perform as well as models trained with unidirectional topK SGD while yielding significant communication benefits for large numbers of workers.

Neural Lyapunov Control of Unknown Nonlinear Systems with Stability Guarantees

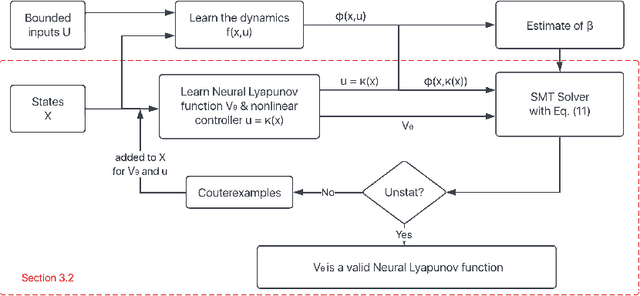
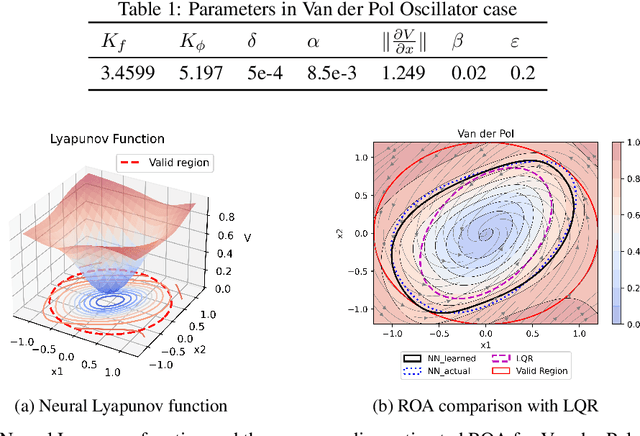
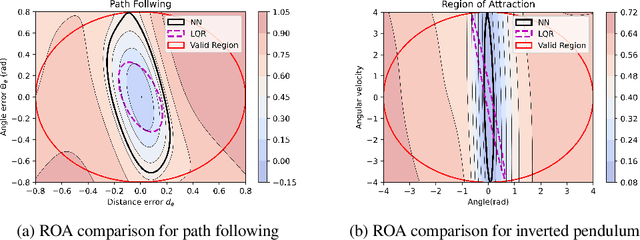
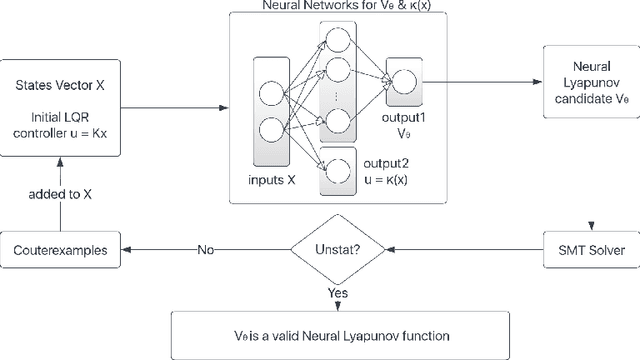
Learning for control of dynamical systems with formal guarantees remains a challenging task. This paper proposes a learning framework to simultaneously stabilize an unknown nonlinear system with a neural controller and learn a neural Lyapunov function to certify a region of attraction (ROA) for the closed-loop system. The algorithmic structure consists of two neural networks and a satisfiability modulo theories (SMT) solver. The first neural network is responsible for learning the unknown dynamics. The second neural network aims to identify a valid Lyapunov function and a provably stabilizing nonlinear controller. The SMT solver then verifies that the candidate Lyapunov function indeed satisfies the Lyapunov conditions. We provide theoretical guarantees of the proposed learning framework in terms of the closed-loop stability for the unknown nonlinear system. We illustrate the effectiveness of the approach with a set of numerical experiments.

Anderson Acceleration as a Krylov Method with Application to Asymptotic Convergence Analysis

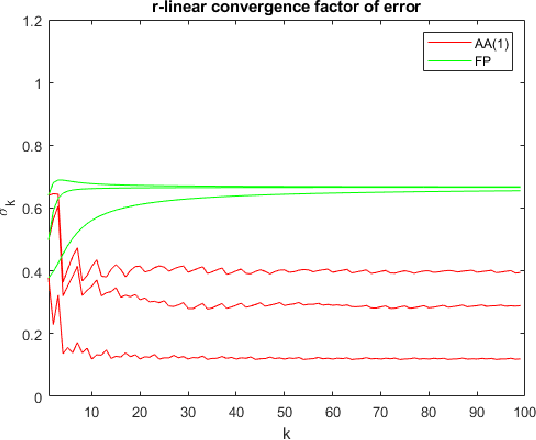
Anderson acceleration is widely used for accelerating the convergence of fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in \mathbb{R}^n$. We consider the case of linear fixed-point methods $x_{k+1}=M x_{k}+b$ and obtain polynomial residual update formulas for AA($m$), i.e., Anderson acceleration with window size $m$. We find that the standard AA($m$) method with initial iterates $x_k$, $k=0, \ldots, m$ defined recursively using AA($k$), is a Krylov space method. This immediately implies that $k$ iterations of AA($m$) cannot produce a smaller residual than $k$ iterations of GMRES without restart (but without implying anything about the relative convergence speed of (windowed) AA($m$) versus restarted GMRES($m$)). We introduce the notion of multi-Krylov method and show that AA($m$) with general initial iterates $\{x_0, \ldots, x_m\}$ is a multi-Krylov method. We find that the AA($m$) residual polynomials observe a periodic memory effect where increasing powers of the error iteration matrix $M$ act on the initial residual as the iteration number increases. We derive several further results based on these polynomial residual update formulas, including orthogonality relations, a lower bound on the AA(1) acceleration coefficient $\beta_k$, and explicit nonlinear recursions for the AA(1) residuals and residual polynomials that do not include the acceleration coefficient $\beta_k$. We apply these results to study the influence of the initial guess on the asymptotic convergence factor of AA(1).

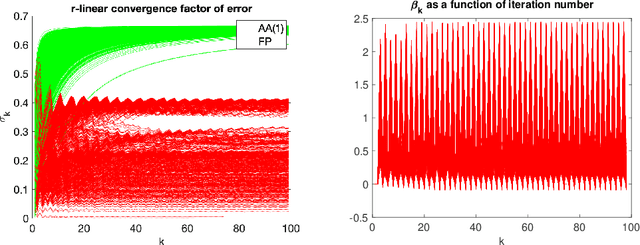
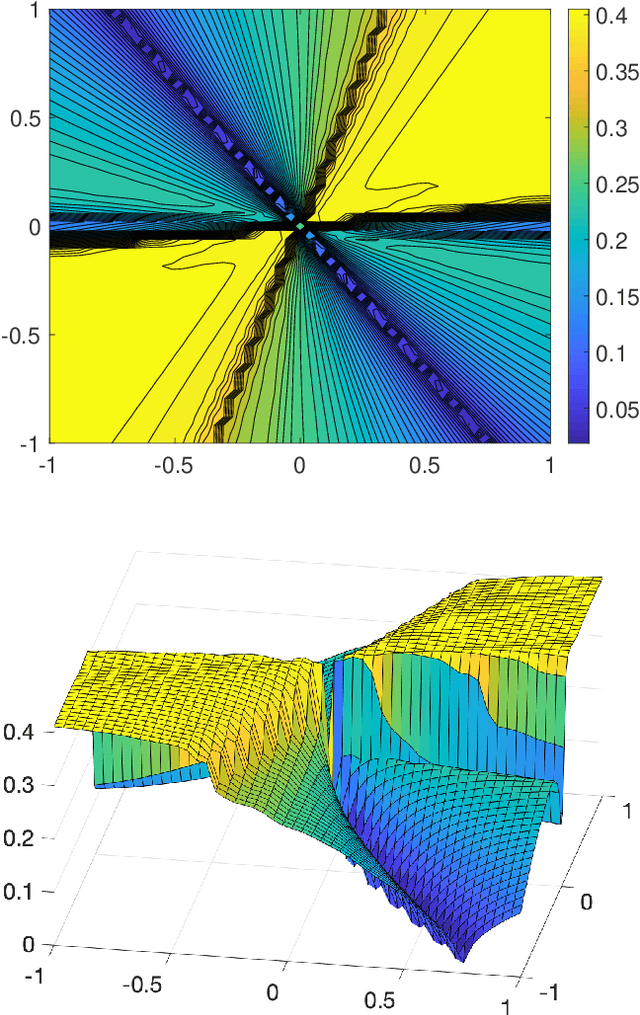
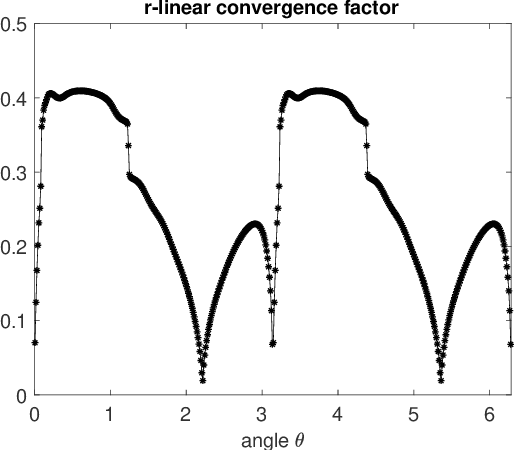
Linear Asymptotic Convergence of Anderson Acceleration: Fixed-Point Analysis

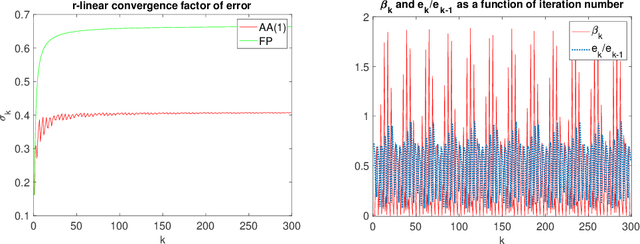
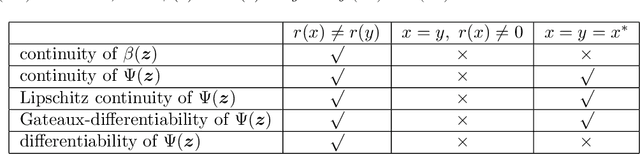
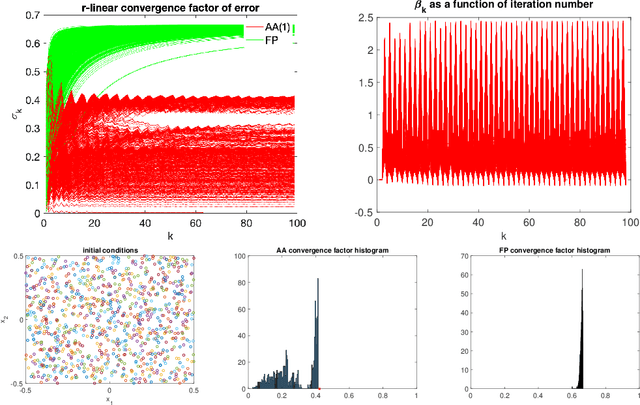
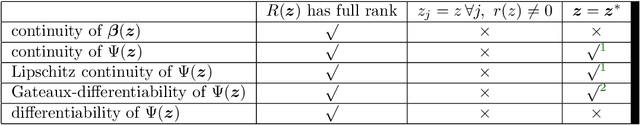
We study the asymptotic convergence of AA($m$), i.e., Anderson acceleration with window size $m$ for accelerating fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in R^n$. Convergence acceleration by AA($m$) has been widely observed but is not well understood. We consider the case where the fixed-point iteration function $q(x)$ is differentiable and the convergence of the fixed-point method itself is root-linear. We identify numerically several conspicuous properties of AA($m$) convergence: First, AA($m$) sequences $\{x_k\}$ converge root-linearly but the root-linear convergence factor depends strongly on the initial condition. Second, the AA($m$) acceleration coefficients $\beta^{(k)}$ do not converge but oscillate as $\{x_k\}$ converges to $x^*$. To shed light on these observations, we write the AA($m$) iteration as an augmented fixed-point iteration $z_{k+1} =\Psi(z_k)$, $z_k \in R^{n(m+1)}$ and analyze the continuity and differentiability properties of $\Psi(z)$ and $\beta(z)$. We find that the vector of acceleration coefficients $\beta(z)$ is not continuous at the fixed point $z^*$. However, we show that, despite the discontinuity of $\beta(z)$, the iteration function $\Psi(z)$ is Lipschitz continuous and directionally differentiable at $z^*$ for AA(1), and we generalize this to AA($m$) with $m>1$ for most cases. Furthermore, we find that $\Psi(z)$ is not differentiable at $z^*$. We then discuss how these theoretical findings relate to the observed convergence behaviour of AA($m$). The discontinuity of $\beta(z)$ at $z^*$ allows $\beta^{(k)}$ to oscillate as $\{x_k\}$ converges to $x^*$, and the non-differentiability of $\Psi(z)$ allows AA($m$) sequences to converge with root-linear convergence factors that strongly depend on the initial condition. Additional numerical results illustrate our findings.

N-ODE Transformer: A Depth-Adaptive Variant of the Transformer Using Neural Ordinary Differential Equations

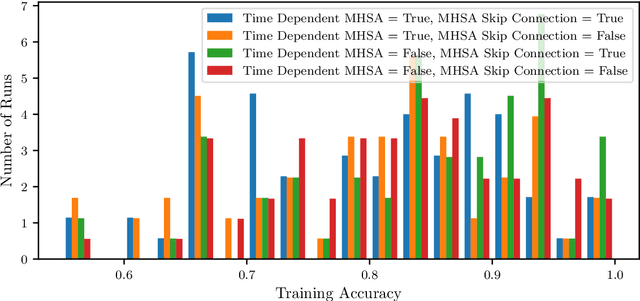
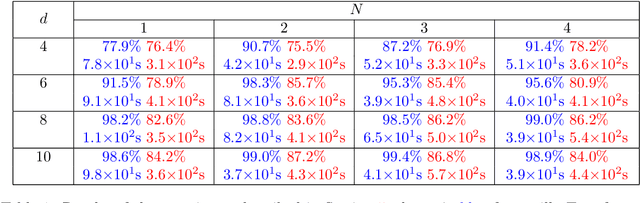
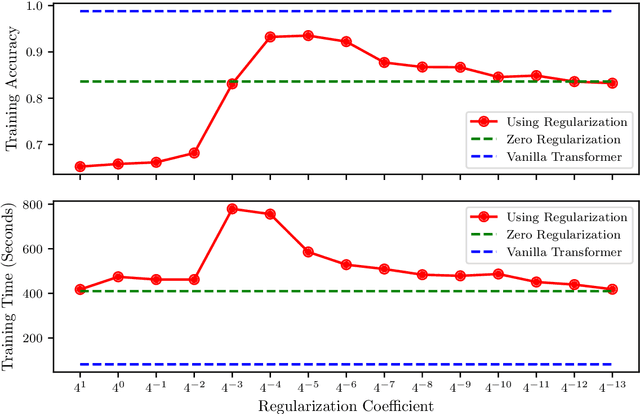
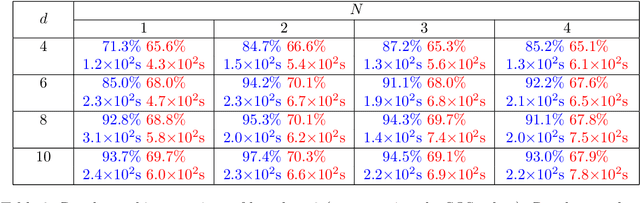
We use neural ordinary differential equations to formulate a variant of the Transformer that is depth-adaptive in the sense that an input-dependent number of time steps is taken by the ordinary differential equation solver. Our goal in proposing the N-ODE Transformer is to investigate whether its depth-adaptivity may aid in overcoming some specific known theoretical limitations of the Transformer in handling nonlocal effects. Specifically, we consider the simple problem of determining the parity of a binary sequence, for which the standard Transformer has known limitations that can only be overcome by using a sufficiently large number of layers or attention heads. We find, however, that the depth-adaptivity of the N-ODE Transformer does not provide a remedy for the inherently nonlocal nature of the parity problem, and provide explanations for why this is so. Next, we pursue regularization of the N-ODE Transformer by penalizing the arclength of the ODE trajectories, but find that this fails to improve the accuracy or efficiency of the N-ODE Transformer on the challenging parity problem. We suggest future avenues of research for modifications and extensions of the N-ODE Transformer that may lead to improved accuracy and efficiency for sequence modelling tasks such as neural machine translation.

On the Asymptotic Linear Convergence Speed of Anderson Acceleration, Nesterov Acceleration, and Nonlinear GMRES

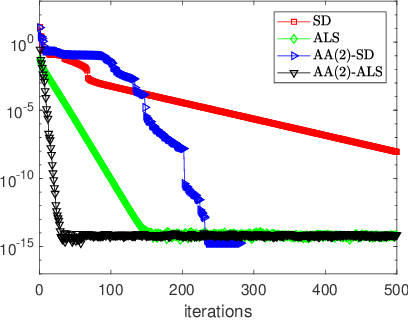
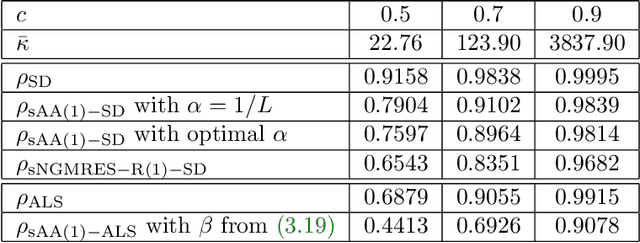
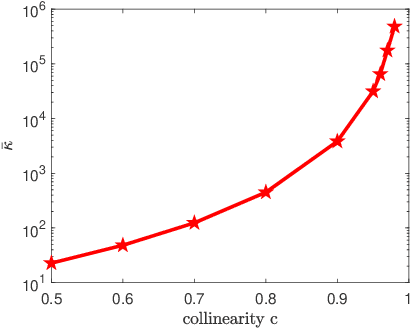
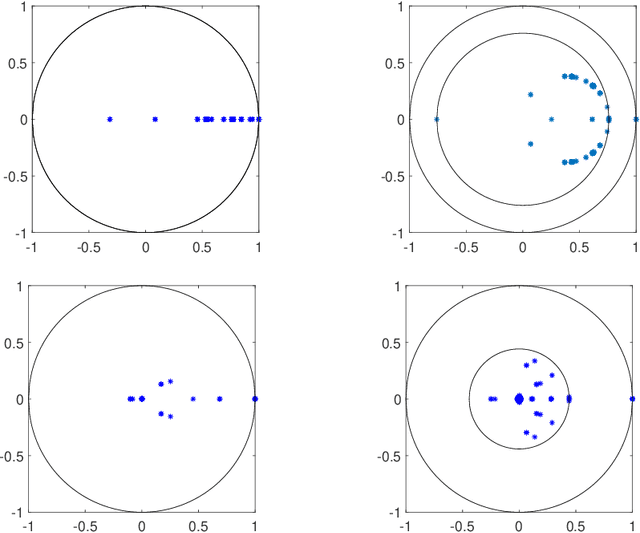
We consider nonlinear convergence acceleration methods for fixed-point iteration $x_{k+1}=q(x_k)$, including Anderson acceleration (AA), nonlinear GMRES (NGMRES), and Nesterov-type acceleration (corresponding to AA with window size one). We focus on fixed-point methods that converge asymptotically linearly with convergence factor $\rho<1$ and that solve an underlying fully smooth and non-convex optimization problem. It is often observed that AA and NGMRES substantially improve the asymptotic convergence behavior of the fixed-point iteration, but this improvement has not been quantified theoretically. We investigate this problem under simplified conditions. First, we consider stationary versions of AA and NGMRES, and determine coefficients that result in optimal asymptotic convergence factors, given knowledge of the spectrum of $q'(x)$ at the fixed point $x^*$. This allows us to understand and quantify the asymptotic convergence improvement that can be provided by nonlinear convergence acceleration, viewing $x_{k+1}=q(x_k)$ as a nonlinear preconditioner for AA and NGMRES. Second, for the case of infinite window size, we consider linear asymptotic convergence bounds for GMRES applied to the fixed-point iteration linearized about $x^*$. Since AA and NGMRES are equivalent to GMRES in the linear case, one may expect the GMRES convergence factors to be relevant for AA and NGMRES as $x_k \rightarrow x^*$. Our results are illustrated numerically for a class of test problems from canonical tensor decomposition, comparing steepest descent and alternating least squares (ALS) as the fixed-point iterations that are accelerated by AA and NGMRES. Our numerical tests show that both approaches allow us to estimate asymptotic convergence speed for nonstationary AA and NGMRES with finite window size.