Learning Koopman-based Stability Certificates for Unknown Nonlinear Systems

Koopman operator theory has gained significant attention in recent years for identifying discrete-time nonlinear systems by embedding them into an infinite-dimensional linear vector space. However, providing stability guarantees while learning the continuous-time dynamics, especially under conditions of relatively low observation frequency, remains a challenge within the existing Koopman-based learning frameworks. To address this challenge, we propose an algorithmic framework to simultaneously learn the vector field and Lyapunov functions for unknown nonlinear systems, using a limited amount of data sampled across the state space and along the trajectories at a relatively low sampling frequency. The proposed framework builds upon recently developed high-accuracy Koopman generator learning for capturing transient system transitions and physics-informed neural networks for training Lyapunov functions. We show that the learned Lyapunov functions can be formally verified using a satisfiability modulo theories (SMT) solver and provide less conservative estimates of the region of attraction compared to existing methods.

Formally Verified Physics-Informed Neural Control Lyapunov Functions

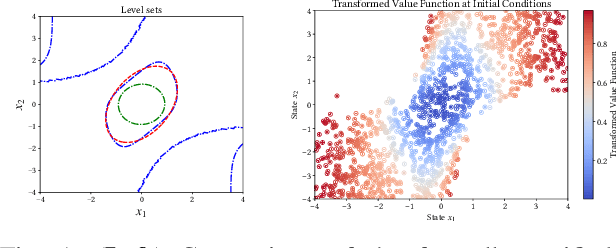
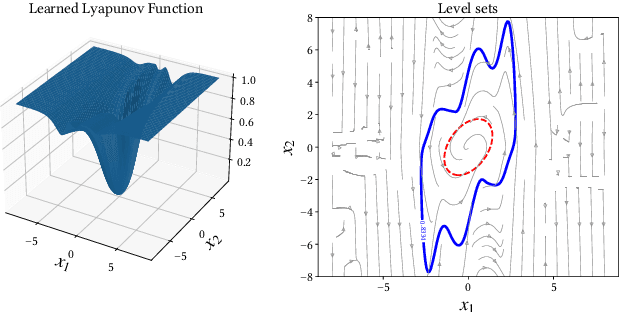
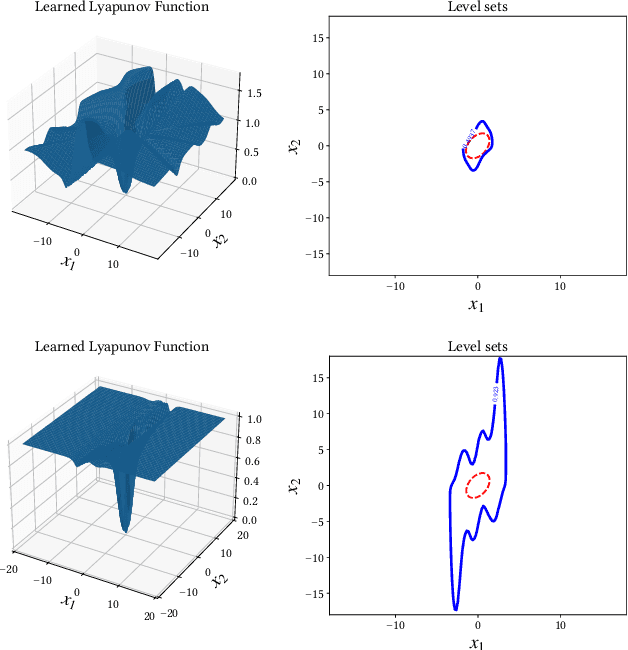
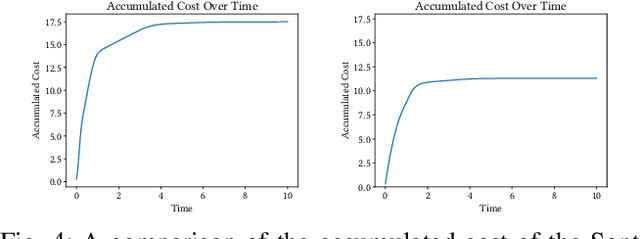
Control Lyapunov functions are a central tool in the design and analysis of stabilizing controllers for nonlinear systems. Constructing such functions, however, remains a significant challenge. In this paper, we investigate physics-informed learning and formal verification of neural network control Lyapunov functions. These neural networks solve a transformed Hamilton-Jacobi-Bellman equation, augmented by data generated using Pontryagin's maximum principle. Similar to how Zubov's equation characterizes the domain of attraction for autonomous systems, this equation characterizes the null-controllability set of a controlled system. This principled learning of neural network control Lyapunov functions outperforms alternative approaches, such as sum-of-squares and rational control Lyapunov functions, as demonstrated by numerical examples. As an intermediate step, we also present results on the formal verification of quadratic control Lyapunov functions, which, aided by satisfiability modulo theories solvers, can perform surprisingly well compared to more sophisticated approaches and efficiently produce global certificates of null-controllability.

Stochastic Reinforcement Learning with Stability Guarantees for Control of Unknown Nonlinear Systems

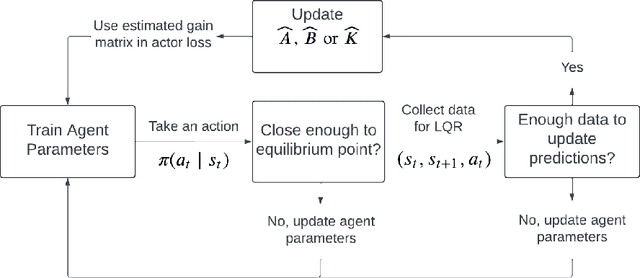
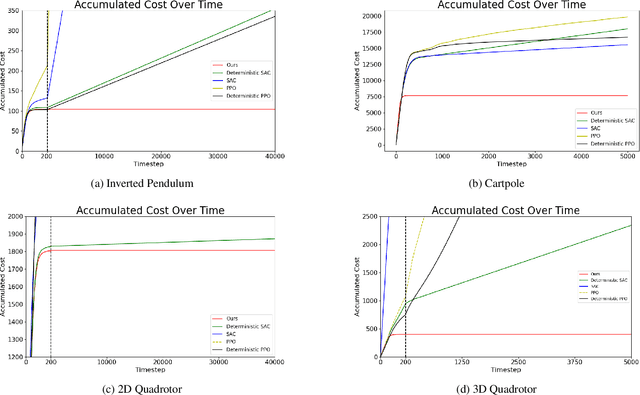
Designing a stabilizing controller for nonlinear systems is a challenging task, especially for high-dimensional problems with unknown dynamics. Traditional reinforcement learning algorithms applied to stabilization tasks tend to drive the system close to the equilibrium point. However, these approaches often fall short of achieving true stabilization and result in persistent oscillations around the equilibrium point. In this work, we propose a reinforcement learning algorithm that stabilizes the system by learning a local linear representation ofthe dynamics. The main component of the algorithm is integrating the learned gain matrix directly into the neural policy. We demonstrate the effectiveness of our algorithm on several challenging high-dimensional dynamical systems. In these simulations, our algorithm outperforms popular reinforcement learning algorithms, such as soft actor-critic (SAC) and proximal policy optimization (PPO), and successfully stabilizes the system. To support the numerical results, we provide a theoretical analysis of the feasibility of the learned algorithm for both deterministic and stochastic reinforcement learning settings, along with a convergence analysis of the proposed learning algorithm. Furthermore, we verify that the learned control policies indeed provide asymptotic stability for the nonlinear systems.

A Model-Free Kullback-Leibler Divergence Filter for Anomaly Detection in Noisy Data Series

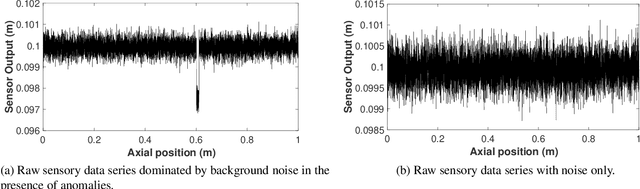
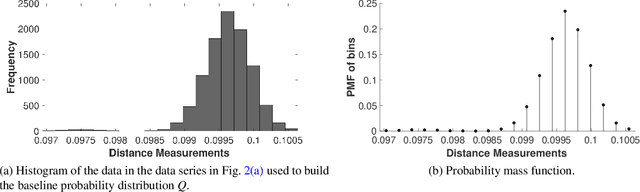
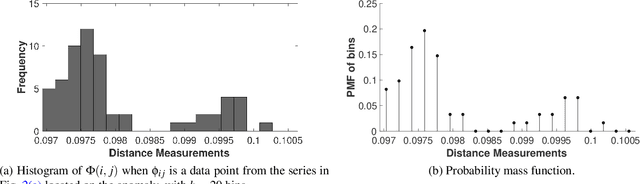
We propose a Kullback-Leibler Divergence (KLD) filter to extract anomalies within data series generated by a broad class of proximity sensors, along with the anomaly locations and their relative sizes. The technique applies to devices commonly used in engineering practice, such as those mounted on mobile robots for non-destructive inspection of hazardous or other environments that may not be directly accessible to humans. The raw data generated by this class of sensors can be challenging to analyze due to the prevalence of noise over the signal content. The proposed filter is built to detect the difference of information content between data series collected by the sensor and baseline data series. It is applicable in a model-based or model-free context. The performance of the KLD filter is validated in an industrial-norm setup and benchmarked against a peer industrially-adopted algorithm.

LyZNet: A Lightweight Python Tool for Learning and Verifying Neural Lyapunov Functions and Regions of Attraction

In this paper, we describe a lightweight Python framework that provides integrated learning and verification of neural Lyapunov functions for stability analysis. The proposed tool, named LyZNet, learns neural Lyapunov functions using physics-informed neural networks (PINNs) to solve Zubov's equation and verifies them using satisfiability modulo theories (SMT) solvers. What distinguishes this tool from others in the literature is its ability to provide verified regions of attraction close to the domain of attraction. This is achieved by encoding Zubov's partial differential equation (PDE) into the PINN approach. By embracing the non-convex nature of the underlying optimization problems, we demonstrate that in cases where convex optimization, such as semidefinite programming, fails to capture the domain of attraction, our neural network framework proves more successful. The tool also offers automatic decomposition of coupled nonlinear systems into a network of low-dimensional subsystems for compositional verification. We illustrate the tool's usage and effectiveness with several numerical examples, including both non-trivial low-dimensional nonlinear systems and high-dimensional systems. The repository of the tool can be found at https://git.uwaterloo.ca/hybrid-systems-lab/lyznet.

Physics-Informed Neural Network Lyapunov Functions: PDE Characterization, Learning, and Verification

We provide a systematic investigation of using physics-informed neural networks to compute Lyapunov functions. We encode Lyapunov conditions as a partial differential equation (PDE) and use this for training neural network Lyapunov functions. We analyze the analytical properties of the solutions to the Lyapunov and Zubov PDEs. In particular, we show that employing the Zubov equation in training neural Lyapunov functions can lead to approximate regions of attraction close to the true domain of attraction. We also examine approximation errors and the convergence of neural approximations to the unique solution of Zubov's equation. We then provide sufficient conditions for the learned neural Lyapunov functions that can be readily verified by satisfiability modulo theories (SMT) solvers, enabling formal verification of both local stability analysis and region-of-attraction estimates in the large. Through a number of nonlinear examples, ranging from low to high dimensions, we demonstrate that the proposed framework can outperform traditional sums-of-squares (SOS) Lyapunov functions obtained using semidefinite programming (SDP).

Harmonic Control Lyapunov Barrier Functions for Constrained Optimal Control with Reach-Avoid Specifications

This paper introduces harmonic control Lyapunov barrier functions (harmonic CLBF) that aid in constrained control problems such as reach-avoid problems. Harmonic CLBFs exploit the maximum principle that harmonic functions satisfy to encode the properties of control Lyapunov barrier functions (CLBFs). As a result, they can be initiated at the start of an experiment rather than trained based on sample trajectories. The control inputs are selected to maximize the inner product of the system dynamics with the steepest descent direction of the harmonic CLBF. Numerical results are presented with four different systems under different reach-avoid environments. Harmonic CLBFs show a significantly low risk of entering unsafe regions and a high probability of entering the goal region.

Neural Lyapunov Control of Unknown Nonlinear Systems with Stability Guarantees

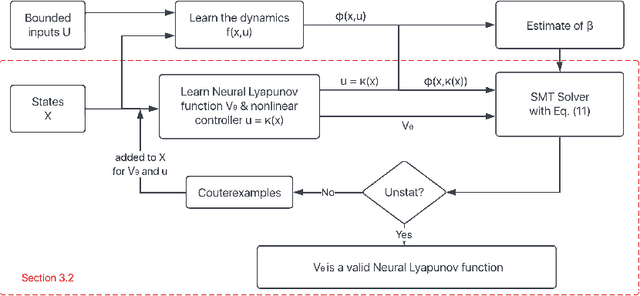
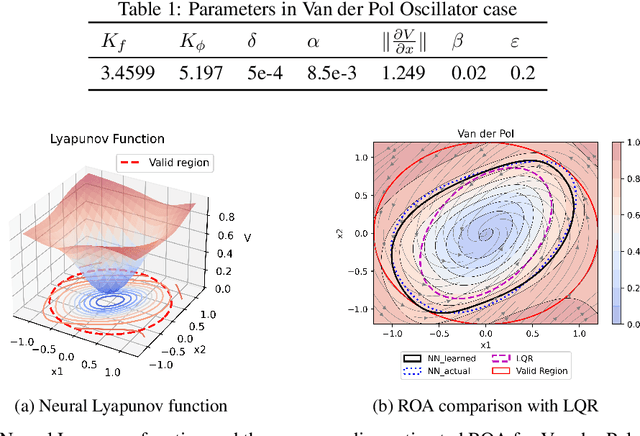
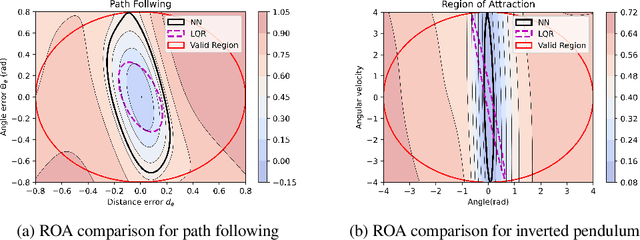
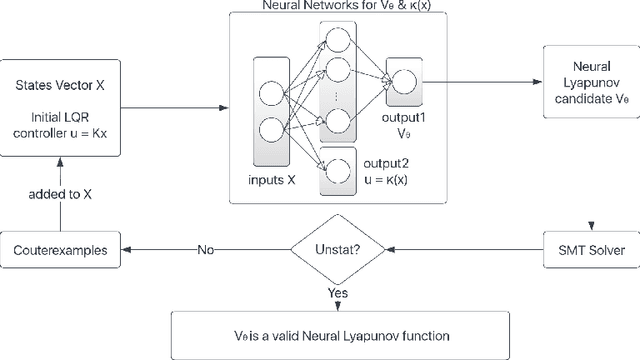
Learning for control of dynamical systems with formal guarantees remains a challenging task. This paper proposes a learning framework to simultaneously stabilize an unknown nonlinear system with a neural controller and learn a neural Lyapunov function to certify a region of attraction (ROA) for the closed-loop system. The algorithmic structure consists of two neural networks and a satisfiability modulo theories (SMT) solver. The first neural network is responsible for learning the unknown dynamics. The second neural network aims to identify a valid Lyapunov function and a provably stabilizing nonlinear controller. The SMT solver then verifies that the candidate Lyapunov function indeed satisfies the Lyapunov conditions. We provide theoretical guarantees of the proposed learning framework in terms of the closed-loop stability for the unknown nonlinear system. We illustrate the effectiveness of the approach with a set of numerical experiments.