Signal Temporal Logic Planning with Time-Varying Robustness

This letter aims to generate a continuous-time trajectory consisting of piecewise B\'ezier curves that satisfy signal temporal logic (STL) specifications with piecewise time-varying robustness. Our time-varying robustness is less conservative than the real-valued robustness, which enables more effective tracking in practical applications. Specifically, our continuous-time trajectories account for dynamic feasibility, leading to smaller tracking errors and ensuring that the STL specifications can be met by the tracking trajectory. Comparative experiments demonstrate the efficiency and effectiveness of the proposed approach.

Stochastic Reinforcement Learning with Stability Guarantees for Control of Unknown Nonlinear Systems

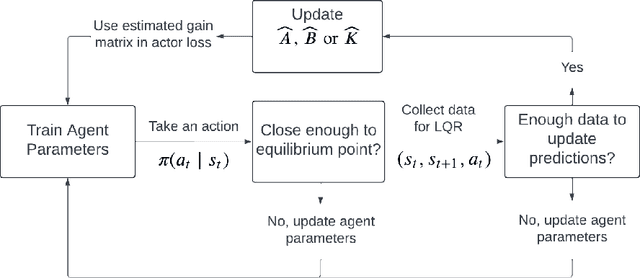
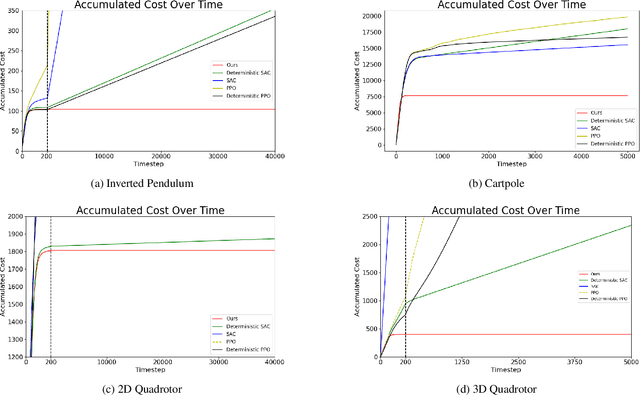
Designing a stabilizing controller for nonlinear systems is a challenging task, especially for high-dimensional problems with unknown dynamics. Traditional reinforcement learning algorithms applied to stabilization tasks tend to drive the system close to the equilibrium point. However, these approaches often fall short of achieving true stabilization and result in persistent oscillations around the equilibrium point. In this work, we propose a reinforcement learning algorithm that stabilizes the system by learning a local linear representation ofthe dynamics. The main component of the algorithm is integrating the learned gain matrix directly into the neural policy. We demonstrate the effectiveness of our algorithm on several challenging high-dimensional dynamical systems. In these simulations, our algorithm outperforms popular reinforcement learning algorithms, such as soft actor-critic (SAC) and proximal policy optimization (PPO), and successfully stabilizes the system. To support the numerical results, we provide a theoretical analysis of the feasibility of the learned algorithm for both deterministic and stochastic reinforcement learning settings, along with a convergence analysis of the proposed learning algorithm. Furthermore, we verify that the learned control policies indeed provide asymptotic stability for the nonlinear systems.

Manifold-Guided Lyapunov Control with Diffusion Models

This paper presents a novel approach to generating stabilizing controllers for a large class of dynamical systems using diffusion models. The core objective is to develop stabilizing control functions by identifying the closest asymptotically stable vector field relative to a predetermined manifold and adjusting the control function based on this finding. To achieve this, we employ a diffusion model trained on pairs consisting of asymptotically stable vector fields and their corresponding Lyapunov functions. Our numerical results demonstrate that this pre-trained model can achieve stabilization over previously unseen systems efficiently and rapidly, showcasing the potential of our approach in fast zero-shot control and generalizability.

Neural Lyapunov Control of Unknown Nonlinear Systems with Stability Guarantees

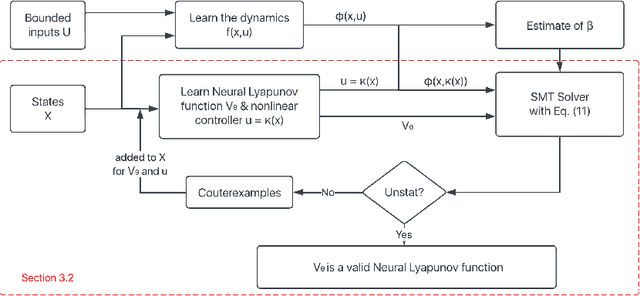
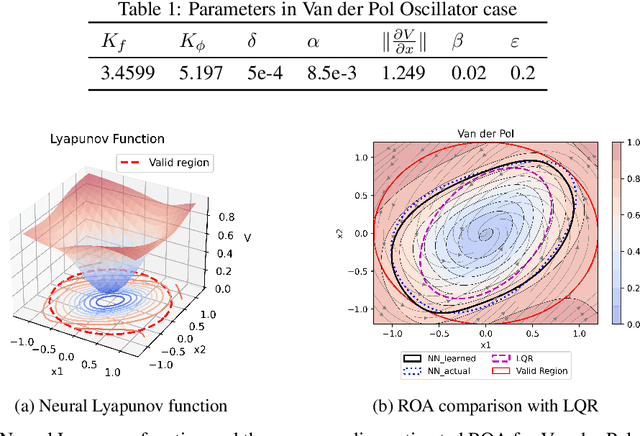
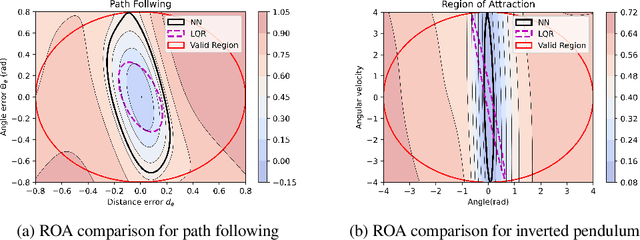
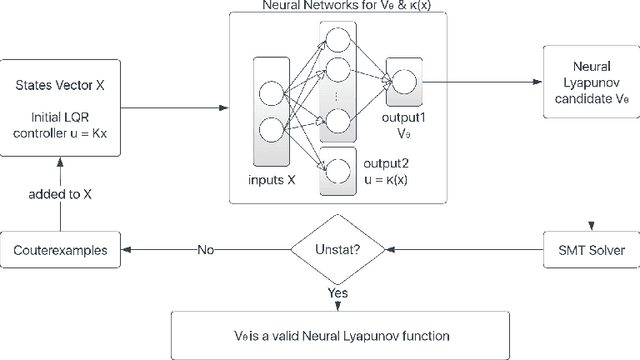
Learning for control of dynamical systems with formal guarantees remains a challenging task. This paper proposes a learning framework to simultaneously stabilize an unknown nonlinear system with a neural controller and learn a neural Lyapunov function to certify a region of attraction (ROA) for the closed-loop system. The algorithmic structure consists of two neural networks and a satisfiability modulo theories (SMT) solver. The first neural network is responsible for learning the unknown dynamics. The second neural network aims to identify a valid Lyapunov function and a provably stabilizing nonlinear controller. The SMT solver then verifies that the candidate Lyapunov function indeed satisfies the Lyapunov conditions. We provide theoretical guarantees of the proposed learning framework in terms of the closed-loop stability for the unknown nonlinear system. We illustrate the effectiveness of the approach with a set of numerical experiments.