Stochastic Reinforcement Learning with Stability Guarantees for Control of Unknown Nonlinear Systems
Paper and Code
Sep 12, 2024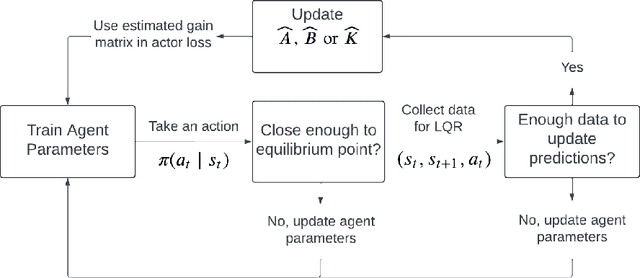
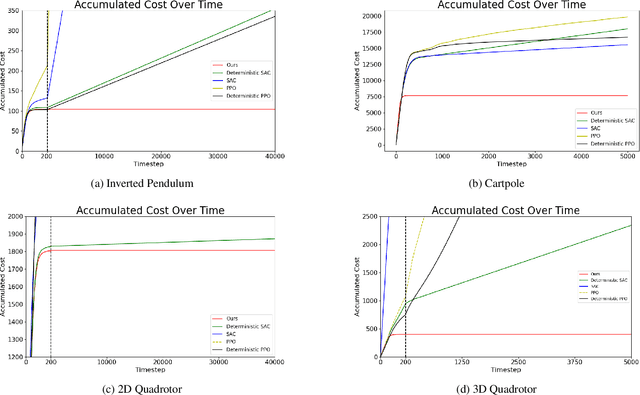

Designing a stabilizing controller for nonlinear systems is a challenging task, especially for high-dimensional problems with unknown dynamics. Traditional reinforcement learning algorithms applied to stabilization tasks tend to drive the system close to the equilibrium point. However, these approaches often fall short of achieving true stabilization and result in persistent oscillations around the equilibrium point. In this work, we propose a reinforcement learning algorithm that stabilizes the system by learning a local linear representation ofthe dynamics. The main component of the algorithm is integrating the learned gain matrix directly into the neural policy. We demonstrate the effectiveness of our algorithm on several challenging high-dimensional dynamical systems. In these simulations, our algorithm outperforms popular reinforcement learning algorithms, such as soft actor-critic (SAC) and proximal policy optimization (PPO), and successfully stabilizes the system. To support the numerical results, we provide a theoretical analysis of the feasibility of the learned algorithm for both deterministic and stochastic reinforcement learning settings, along with a convergence analysis of the proposed learning algorithm. Furthermore, we verify that the learned control policies indeed provide asymptotic stability for the nonlinear systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge