Manifold-Guided Lyapunov Control with Diffusion Models

This paper presents a novel approach to generating stabilizing controllers for a large class of dynamical systems using diffusion models. The core objective is to develop stabilizing control functions by identifying the closest asymptotically stable vector field relative to a predetermined manifold and adjusting the control function based on this finding. To achieve this, we employ a diffusion model trained on pairs consisting of asymptotically stable vector fields and their corresponding Lyapunov functions. Our numerical results demonstrate that this pre-trained model can achieve stabilization over previously unseen systems efficiently and rapidly, showcasing the potential of our approach in fast zero-shot control and generalizability.

Denoising Diffusion Restoration Tackles Forward and Inverse Problems for the Laplace Operator

Diffusion models have emerged as a promising class of generative models that map noisy inputs to realistic images. More recently, they have been employed to generate solutions to partial differential equations (PDEs). However, they still struggle with inverse problems in the Laplacian operator, for instance, the Poisson equation, because the eigenvalues that are large in magnitude amplify the measurement noise. This paper presents a novel approach for the inverse and forward solution of PDEs through the use of denoising diffusion restoration models (DDRM). DDRMs were used in linear inverse problems to restore original clean signals by exploiting the singular value decomposition (SVD) of the linear operator. Equivalently, we present an approach to restore the solution and the parameters in the Poisson equation by exploiting the eigenvalues and the eigenfunctions of the Laplacian operator. Our results show that using denoising diffusion restoration significantly improves the estimation of the solution and parameters. Our research, as a result, pioneers the integration of diffusion models with the principles of underlying physics to solve PDEs.

Harmonic Control Lyapunov Barrier Functions for Constrained Optimal Control with Reach-Avoid Specifications

This paper introduces harmonic control Lyapunov barrier functions (harmonic CLBF) that aid in constrained control problems such as reach-avoid problems. Harmonic CLBFs exploit the maximum principle that harmonic functions satisfy to encode the properties of control Lyapunov barrier functions (CLBFs). As a result, they can be initiated at the start of an experiment rather than trained based on sample trajectories. The control inputs are selected to maximize the inner product of the system dynamics with the steepest descent direction of the harmonic CLBF. Numerical results are presented with four different systems under different reach-avoid environments. Harmonic CLBFs show a significantly low risk of entering unsafe regions and a high probability of entering the goal region.

Actor-Critic Methods using Physics-Informed Neural Networks: Control of a 1D PDE Model for Fluid-Cooled Battery Packs

This paper proposes an actor-critic algorithm for controlling the temperature of a battery pack using a cooling fluid. This is modeled by a coupled 1D partial differential equation (PDE) with a controlled advection term that determines the speed of the cooling fluid. The Hamilton-Jacobi-Bellman (HJB) equation is a PDE that evaluates the optimality of the value function and determines an optimal controller. We propose an algorithm that treats the value network as a Physics-Informed Neural Network (PINN) to solve for the continuous-time HJB equation rather than a discrete-time Bellman optimality equation, and we derive an optimal controller for the environment that we exploit to achieve optimal control. Our experiments show that a hybrid-policy method that updates the value network using the HJB equation and updates the policy network identically to PPO achieves the best results in the control of this PDE system.

Bridging Physics-Informed Neural Networks with Reinforcement Learning: Hamilton-Jacobi-Bellman Proximal Policy Optimization (HJBPPO)

This paper introduces the Hamilton-Jacobi-Bellman Proximal Policy Optimization (HJBPPO) algorithm into reinforcement learning. The Hamilton-Jacobi-Bellman (HJB) equation is used in control theory to evaluate the optimality of the value function. Our work combines the HJB equation with reinforcement learning in continuous state and action spaces to improve the training of the value network. We treat the value network as a Physics-Informed Neural Network (PINN) to solve for the HJB equation by computing its derivatives with respect to its inputs exactly. The Proximal Policy Optimization (PPO)-Clipped algorithm is improvised with this implementation as it uses a value network to compute the objective function for its policy network. The HJBPPO algorithm shows an improved performance compared to PPO on the MuJoCo environments.

A Comparison of Reward Functions in Q-Learning Applied to a Cart Position Problem

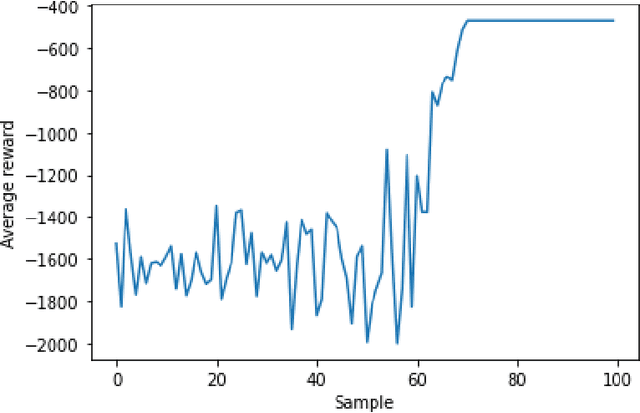
Growing advancements in reinforcement learning has led to advancements in control theory. Reinforcement learning has effectively solved the inverted pendulum problem and more recently the double inverted pendulum problem. In reinforcement learning, our agents learn by interacting with the control system with the goal of maximizing rewards. In this paper, we explore three such reward functions in the cart position problem. This paper concludes that a discontinuous reward function that gives non-zero rewards to agents only if they are within a given distance from the desired position gives the best results.