Formally Verified Physics-Informed Neural Control Lyapunov Functions

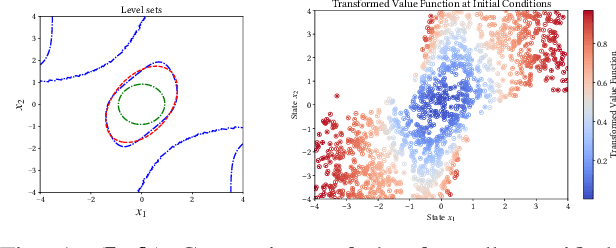
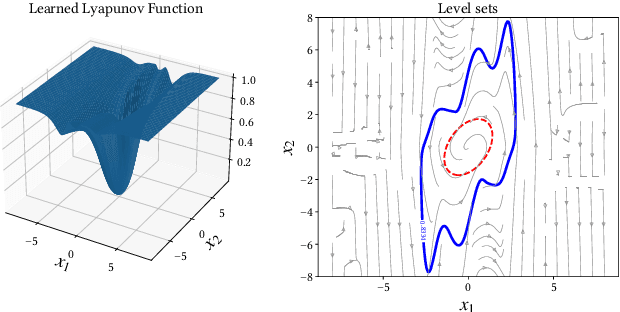
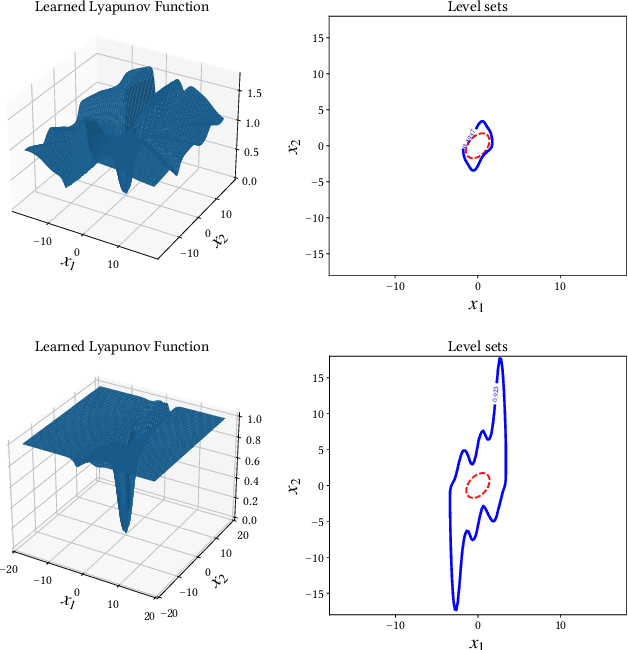
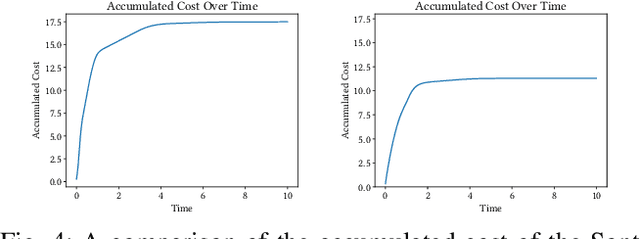
Control Lyapunov functions are a central tool in the design and analysis of stabilizing controllers for nonlinear systems. Constructing such functions, however, remains a significant challenge. In this paper, we investigate physics-informed learning and formal verification of neural network control Lyapunov functions. These neural networks solve a transformed Hamilton-Jacobi-Bellman equation, augmented by data generated using Pontryagin's maximum principle. Similar to how Zubov's equation characterizes the domain of attraction for autonomous systems, this equation characterizes the null-controllability set of a controlled system. This principled learning of neural network control Lyapunov functions outperforms alternative approaches, such as sum-of-squares and rational control Lyapunov functions, as demonstrated by numerical examples. As an intermediate step, we also present results on the formal verification of quadratic control Lyapunov functions, which, aided by satisfiability modulo theories solvers, can perform surprisingly well compared to more sophisticated approaches and efficiently produce global certificates of null-controllability.

LyZNet: A Lightweight Python Tool for Learning and Verifying Neural Lyapunov Functions and Regions of Attraction

In this paper, we describe a lightweight Python framework that provides integrated learning and verification of neural Lyapunov functions for stability analysis. The proposed tool, named LyZNet, learns neural Lyapunov functions using physics-informed neural networks (PINNs) to solve Zubov's equation and verifies them using satisfiability modulo theories (SMT) solvers. What distinguishes this tool from others in the literature is its ability to provide verified regions of attraction close to the domain of attraction. This is achieved by encoding Zubov's partial differential equation (PDE) into the PINN approach. By embracing the non-convex nature of the underlying optimization problems, we demonstrate that in cases where convex optimization, such as semidefinite programming, fails to capture the domain of attraction, our neural network framework proves more successful. The tool also offers automatic decomposition of coupled nonlinear systems into a network of low-dimensional subsystems for compositional verification. We illustrate the tool's usage and effectiveness with several numerical examples, including both non-trivial low-dimensional nonlinear systems and high-dimensional systems. The repository of the tool can be found at https://git.uwaterloo.ca/hybrid-systems-lab/lyznet.

Physics-Informed Neural Network Lyapunov Functions: PDE Characterization, Learning, and Verification

We provide a systematic investigation of using physics-informed neural networks to compute Lyapunov functions. We encode Lyapunov conditions as a partial differential equation (PDE) and use this for training neural network Lyapunov functions. We analyze the analytical properties of the solutions to the Lyapunov and Zubov PDEs. In particular, we show that employing the Zubov equation in training neural Lyapunov functions can lead to approximate regions of attraction close to the true domain of attraction. We also examine approximation errors and the convergence of neural approximations to the unique solution of Zubov's equation. We then provide sufficient conditions for the learned neural Lyapunov functions that can be readily verified by satisfiability modulo theories (SMT) solvers, enabling formal verification of both local stability analysis and region-of-attraction estimates in the large. Through a number of nonlinear examples, ranging from low to high dimensions, we demonstrate that the proposed framework can outperform traditional sums-of-squares (SOS) Lyapunov functions obtained using semidefinite programming (SDP).