Anderson Acceleration as a Krylov Method with Application to Asymptotic Convergence Analysis
Paper and Code
Sep 29, 2021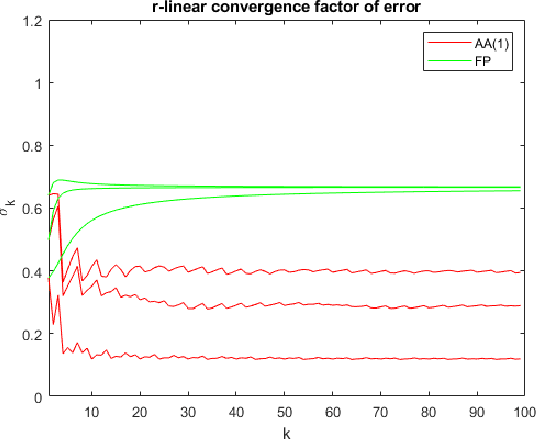
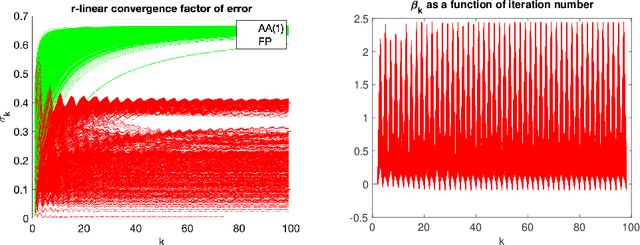
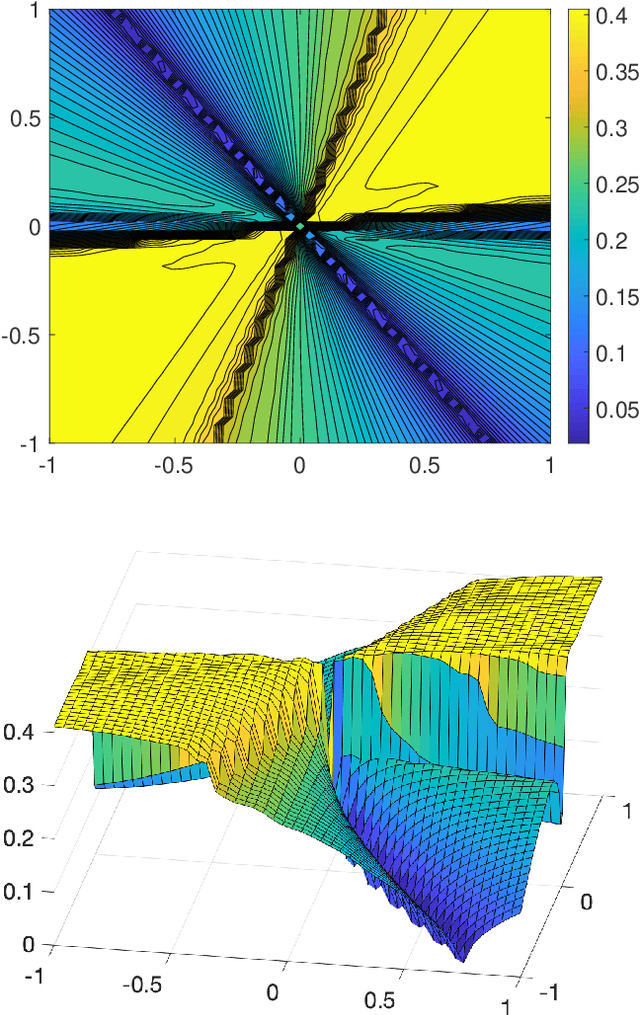
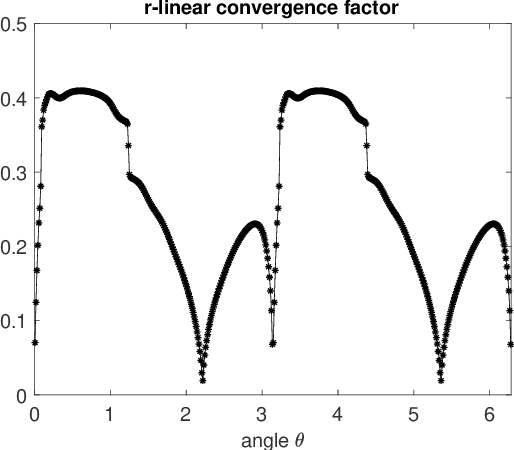
Anderson acceleration is widely used for accelerating the convergence of fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in \mathbb{R}^n$. We consider the case of linear fixed-point methods $x_{k+1}=M x_{k}+b$ and obtain polynomial residual update formulas for AA($m$), i.e., Anderson acceleration with window size $m$. We find that the standard AA($m$) method with initial iterates $x_k$, $k=0, \ldots, m$ defined recursively using AA($k$), is a Krylov space method. This immediately implies that $k$ iterations of AA($m$) cannot produce a smaller residual than $k$ iterations of GMRES without restart (but without implying anything about the relative convergence speed of (windowed) AA($m$) versus restarted GMRES($m$)). We introduce the notion of multi-Krylov method and show that AA($m$) with general initial iterates $\{x_0, \ldots, x_m\}$ is a multi-Krylov method. We find that the AA($m$) residual polynomials observe a periodic memory effect where increasing powers of the error iteration matrix $M$ act on the initial residual as the iteration number increases. We derive several further results based on these polynomial residual update formulas, including orthogonality relations, a lower bound on the AA(1) acceleration coefficient $\beta_k$, and explicit nonlinear recursions for the AA(1) residuals and residual polynomials that do not include the acceleration coefficient $\beta_k$. We apply these results to study the influence of the initial guess on the asymptotic convergence factor of AA(1).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge