Anderson Acceleration as a Krylov Method with Application to Asymptotic Convergence Analysis

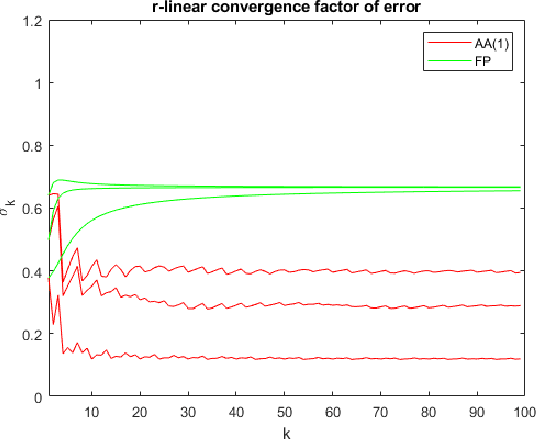
Anderson acceleration is widely used for accelerating the convergence of fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in \mathbb{R}^n$. We consider the case of linear fixed-point methods $x_{k+1}=M x_{k}+b$ and obtain polynomial residual update formulas for AA($m$), i.e., Anderson acceleration with window size $m$. We find that the standard AA($m$) method with initial iterates $x_k$, $k=0, \ldots, m$ defined recursively using AA($k$), is a Krylov space method. This immediately implies that $k$ iterations of AA($m$) cannot produce a smaller residual than $k$ iterations of GMRES without restart (but without implying anything about the relative convergence speed of (windowed) AA($m$) versus restarted GMRES($m$)). We introduce the notion of multi-Krylov method and show that AA($m$) with general initial iterates $\{x_0, \ldots, x_m\}$ is a multi-Krylov method. We find that the AA($m$) residual polynomials observe a periodic memory effect where increasing powers of the error iteration matrix $M$ act on the initial residual as the iteration number increases. We derive several further results based on these polynomial residual update formulas, including orthogonality relations, a lower bound on the AA(1) acceleration coefficient $\beta_k$, and explicit nonlinear recursions for the AA(1) residuals and residual polynomials that do not include the acceleration coefficient $\beta_k$. We apply these results to study the influence of the initial guess on the asymptotic convergence factor of AA(1).

Linear Asymptotic Convergence of Anderson Acceleration: Fixed-Point Analysis

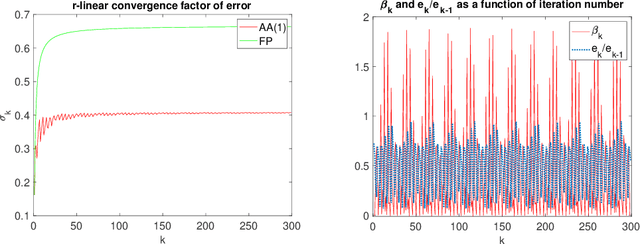
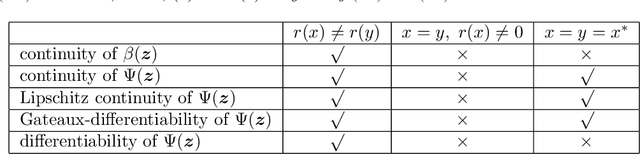
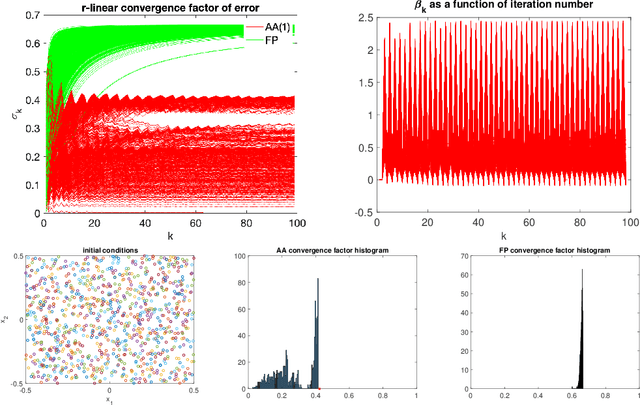
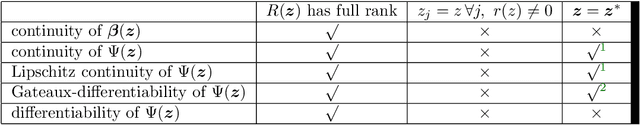
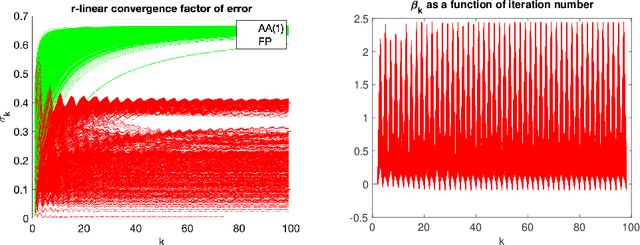
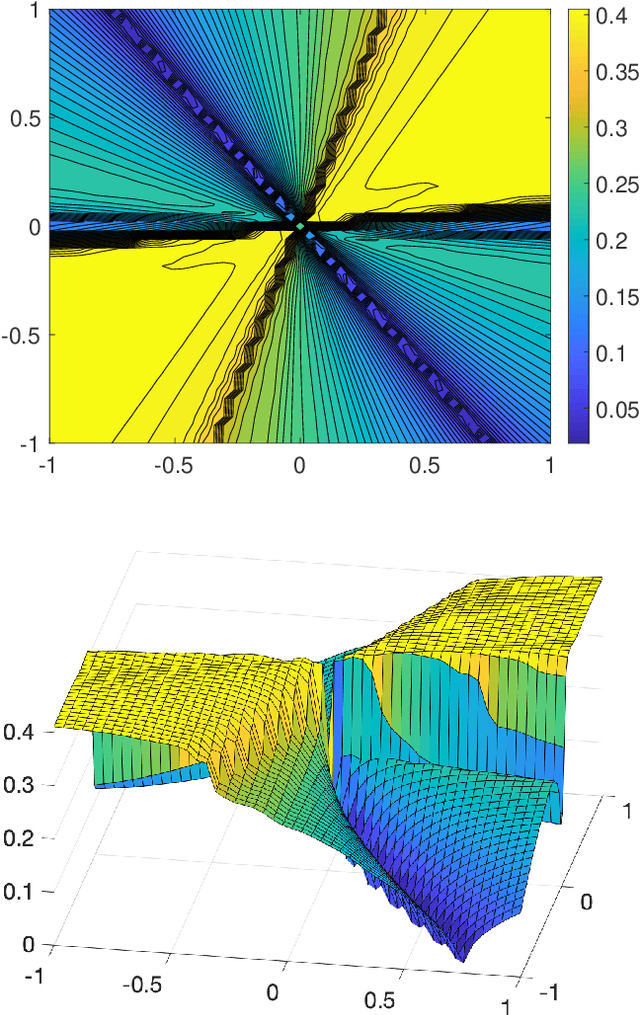
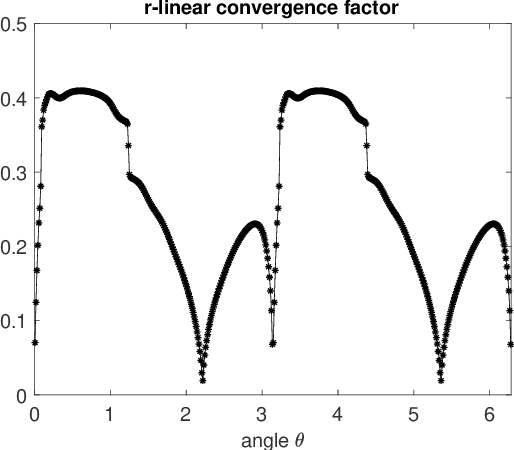
We study the asymptotic convergence of AA($m$), i.e., Anderson acceleration with window size $m$ for accelerating fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in R^n$. Convergence acceleration by AA($m$) has been widely observed but is not well understood. We consider the case where the fixed-point iteration function $q(x)$ is differentiable and the convergence of the fixed-point method itself is root-linear. We identify numerically several conspicuous properties of AA($m$) convergence: First, AA($m$) sequences $\{x_k\}$ converge root-linearly but the root-linear convergence factor depends strongly on the initial condition. Second, the AA($m$) acceleration coefficients $\beta^{(k)}$ do not converge but oscillate as $\{x_k\}$ converges to $x^*$. To shed light on these observations, we write the AA($m$) iteration as an augmented fixed-point iteration $z_{k+1} =\Psi(z_k)$, $z_k \in R^{n(m+1)}$ and analyze the continuity and differentiability properties of $\Psi(z)$ and $\beta(z)$. We find that the vector of acceleration coefficients $\beta(z)$ is not continuous at the fixed point $z^*$. However, we show that, despite the discontinuity of $\beta(z)$, the iteration function $\Psi(z)$ is Lipschitz continuous and directionally differentiable at $z^*$ for AA(1), and we generalize this to AA($m$) with $m>1$ for most cases. Furthermore, we find that $\Psi(z)$ is not differentiable at $z^*$. We then discuss how these theoretical findings relate to the observed convergence behaviour of AA($m$). The discontinuity of $\beta(z)$ at $z^*$ allows $\beta^{(k)}$ to oscillate as $\{x_k\}$ converges to $x^*$, and the non-differentiability of $\Psi(z)$ allows AA($m$) sequences to converge with root-linear convergence factors that strongly depend on the initial condition. Additional numerical results illustrate our findings.

On the Asymptotic Linear Convergence Speed of Anderson Acceleration, Nesterov Acceleration, and Nonlinear GMRES

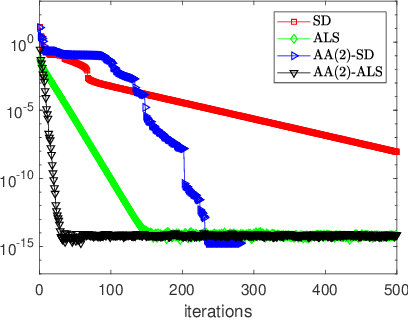
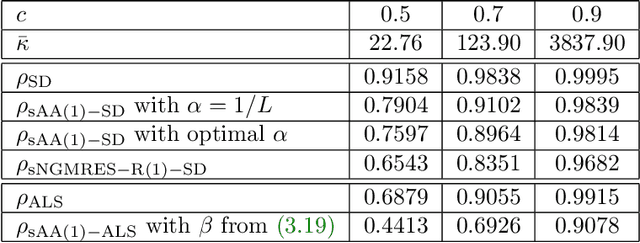
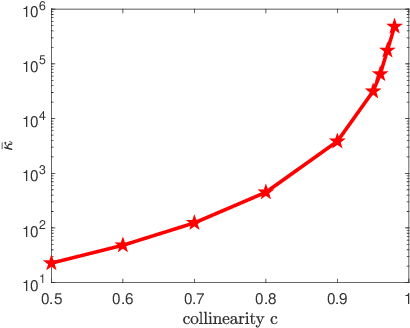
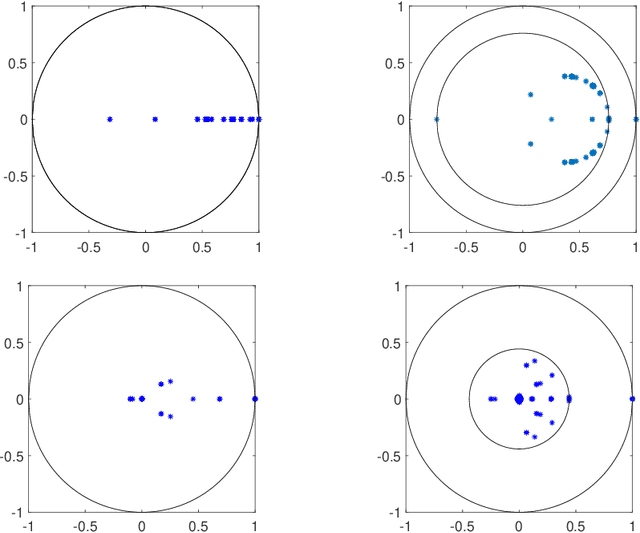
We consider nonlinear convergence acceleration methods for fixed-point iteration $x_{k+1}=q(x_k)$, including Anderson acceleration (AA), nonlinear GMRES (NGMRES), and Nesterov-type acceleration (corresponding to AA with window size one). We focus on fixed-point methods that converge asymptotically linearly with convergence factor $\rho<1$ and that solve an underlying fully smooth and non-convex optimization problem. It is often observed that AA and NGMRES substantially improve the asymptotic convergence behavior of the fixed-point iteration, but this improvement has not been quantified theoretically. We investigate this problem under simplified conditions. First, we consider stationary versions of AA and NGMRES, and determine coefficients that result in optimal asymptotic convergence factors, given knowledge of the spectrum of $q'(x)$ at the fixed point $x^*$. This allows us to understand and quantify the asymptotic convergence improvement that can be provided by nonlinear convergence acceleration, viewing $x_{k+1}=q(x_k)$ as a nonlinear preconditioner for AA and NGMRES. Second, for the case of infinite window size, we consider linear asymptotic convergence bounds for GMRES applied to the fixed-point iteration linearized about $x^*$. Since AA and NGMRES are equivalent to GMRES in the linear case, one may expect the GMRES convergence factors to be relevant for AA and NGMRES as $x_k \rightarrow x^*$. Our results are illustrated numerically for a class of test problems from canonical tensor decomposition, comparing steepest descent and alternating least squares (ALS) as the fixed-point iterations that are accelerated by AA and NGMRES. Our numerical tests show that both approaches allow us to estimate asymptotic convergence speed for nonstationary AA and NGMRES with finite window size.

Quantifying the asymptotic linear convergence speed of Anderson Acceleration applied to ADMM

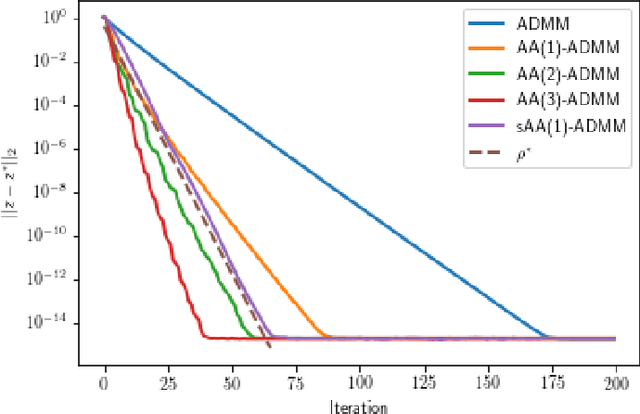
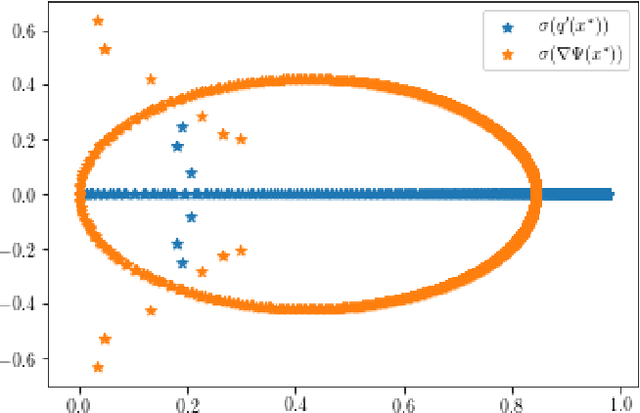
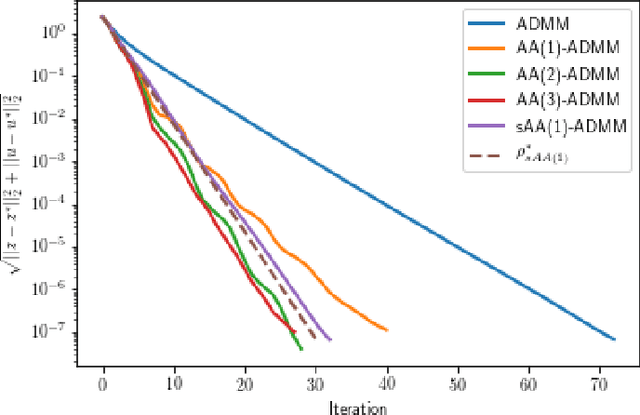
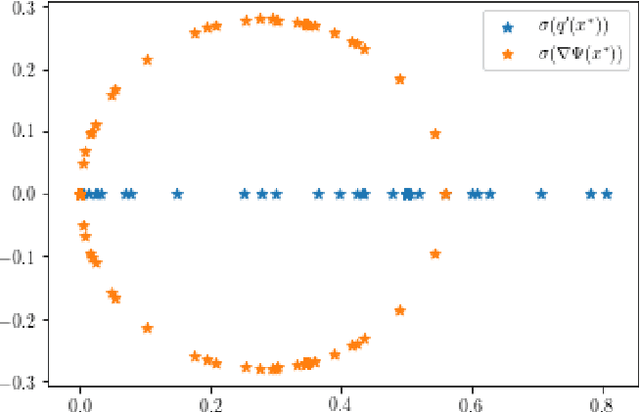
We explain how Anderson Acceleration (AA) speeds up the Alternating Direction Method of Multipliers (ADMM), for the case where ADMM by itself converges linearly. We do so by considering the spectral properties of the Jacobians of ADMM and a stationary version of AA evaluated at the fixed point, where the coefficients of the stationary version are computed such that its asymptotic linear convergence factor is optimal. Numerical tests show that this allows us to quantify the improved linear asymptotic convergence speed of AA-ADMM as compared to the convergence factor of ADMM used by itself. This way of estimating AA-ADMM convergence speed is useful because there are no known convergence bounds for AA with finite window size that would allow quantification of this improvement in asymptotic convergence speed.