Quantifying the asymptotic linear convergence speed of Anderson Acceleration applied to ADMM

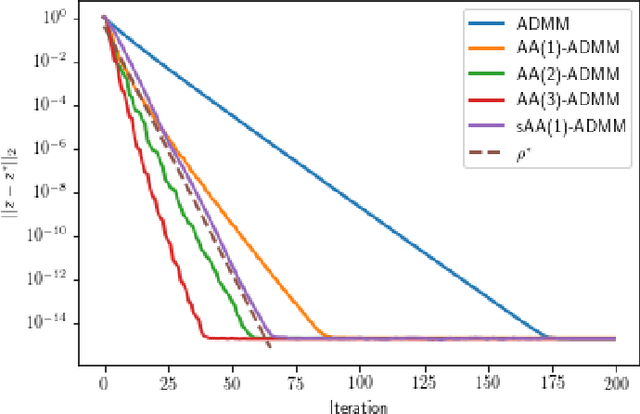
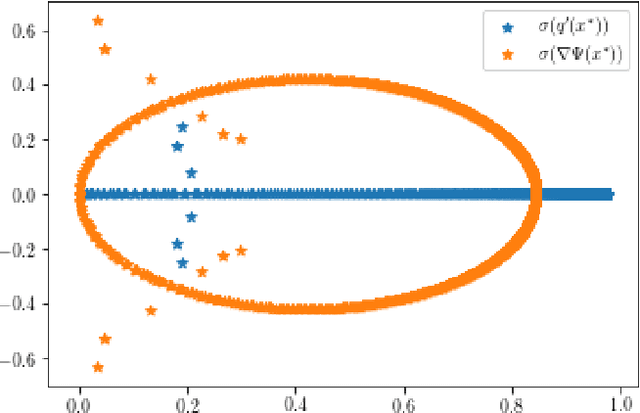
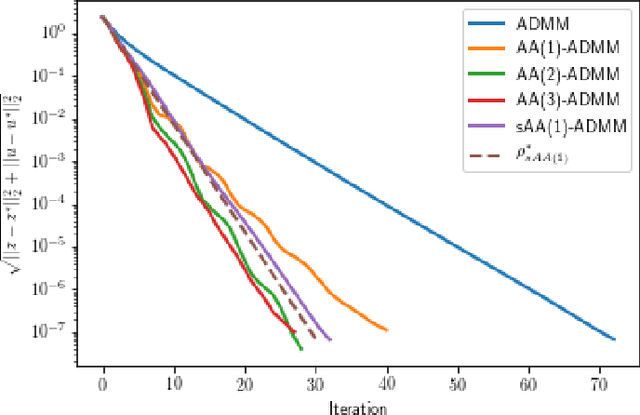
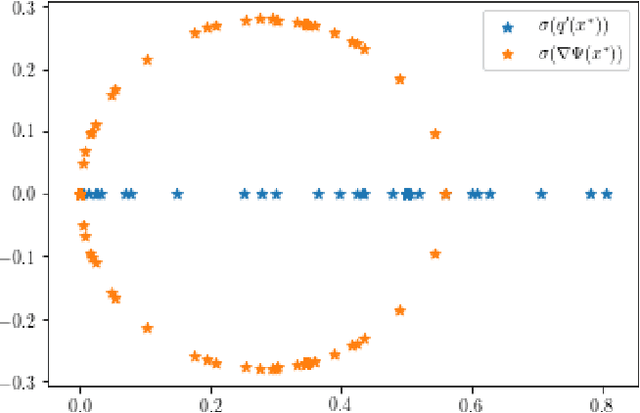
We explain how Anderson Acceleration (AA) speeds up the Alternating Direction Method of Multipliers (ADMM), for the case where ADMM by itself converges linearly. We do so by considering the spectral properties of the Jacobians of ADMM and a stationary version of AA evaluated at the fixed point, where the coefficients of the stationary version are computed such that its asymptotic linear convergence factor is optimal. Numerical tests show that this allows us to quantify the improved linear asymptotic convergence speed of AA-ADMM as compared to the convergence factor of ADMM used by itself. This way of estimating AA-ADMM convergence speed is useful because there are no known convergence bounds for AA with finite window size that would allow quantification of this improvement in asymptotic convergence speed.