Linear Asymptotic Convergence of Anderson Acceleration: Fixed-Point Analysis
Paper and Code
Sep 29, 2021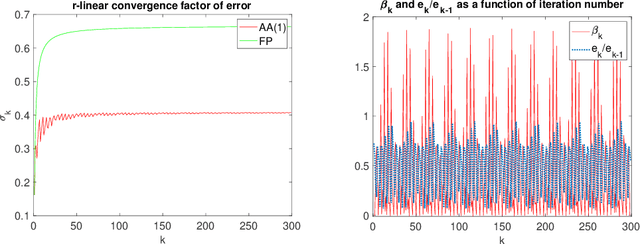
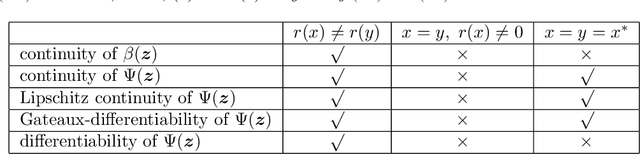
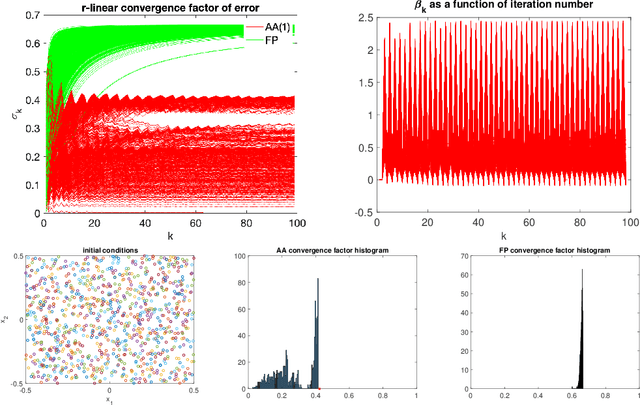
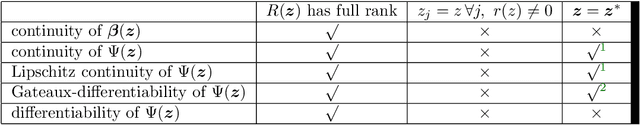
We study the asymptotic convergence of AA($m$), i.e., Anderson acceleration with window size $m$ for accelerating fixed-point methods $x_{k+1}=q(x_{k})$, $x_k \in R^n$. Convergence acceleration by AA($m$) has been widely observed but is not well understood. We consider the case where the fixed-point iteration function $q(x)$ is differentiable and the convergence of the fixed-point method itself is root-linear. We identify numerically several conspicuous properties of AA($m$) convergence: First, AA($m$) sequences $\{x_k\}$ converge root-linearly but the root-linear convergence factor depends strongly on the initial condition. Second, the AA($m$) acceleration coefficients $\beta^{(k)}$ do not converge but oscillate as $\{x_k\}$ converges to $x^*$. To shed light on these observations, we write the AA($m$) iteration as an augmented fixed-point iteration $z_{k+1} =\Psi(z_k)$, $z_k \in R^{n(m+1)}$ and analyze the continuity and differentiability properties of $\Psi(z)$ and $\beta(z)$. We find that the vector of acceleration coefficients $\beta(z)$ is not continuous at the fixed point $z^*$. However, we show that, despite the discontinuity of $\beta(z)$, the iteration function $\Psi(z)$ is Lipschitz continuous and directionally differentiable at $z^*$ for AA(1), and we generalize this to AA($m$) with $m>1$ for most cases. Furthermore, we find that $\Psi(z)$ is not differentiable at $z^*$. We then discuss how these theoretical findings relate to the observed convergence behaviour of AA($m$). The discontinuity of $\beta(z)$ at $z^*$ allows $\beta^{(k)}$ to oscillate as $\{x_k\}$ converges to $x^*$, and the non-differentiability of $\Psi(z)$ allows AA($m$) sequences to converge with root-linear convergence factors that strongly depend on the initial condition. Additional numerical results illustrate our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge