Aaron Baier-Reinio
N-ODE Transformer: A Depth-Adaptive Variant of the Transformer Using Neural Ordinary Differential Equations
Oct 22, 2020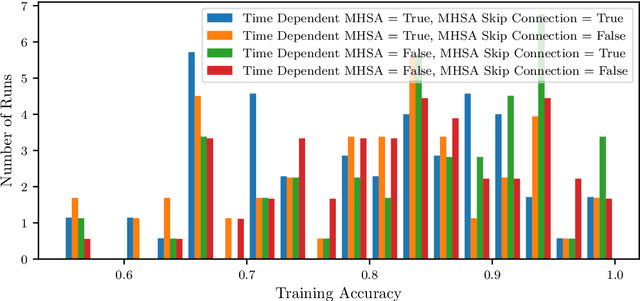
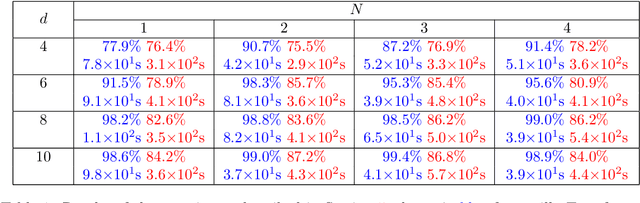
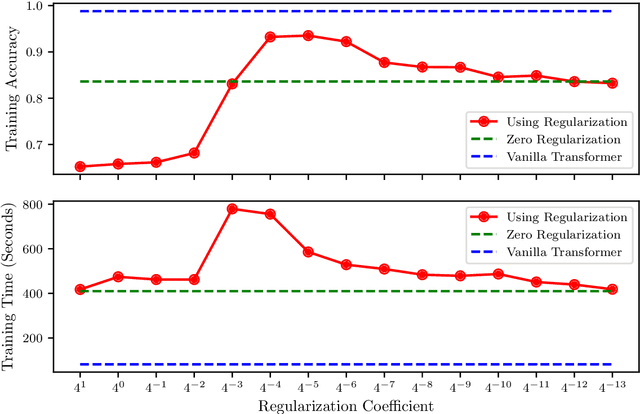
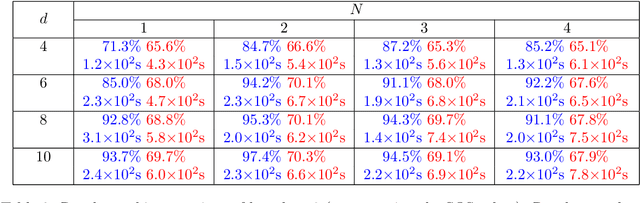
Abstract:We use neural ordinary differential equations to formulate a variant of the Transformer that is depth-adaptive in the sense that an input-dependent number of time steps is taken by the ordinary differential equation solver. Our goal in proposing the N-ODE Transformer is to investigate whether its depth-adaptivity may aid in overcoming some specific known theoretical limitations of the Transformer in handling nonlocal effects. Specifically, we consider the simple problem of determining the parity of a binary sequence, for which the standard Transformer has known limitations that can only be overcome by using a sufficiently large number of layers or attention heads. We find, however, that the depth-adaptivity of the N-ODE Transformer does not provide a remedy for the inherently nonlocal nature of the parity problem, and provide explanations for why this is so. Next, we pursue regularization of the N-ODE Transformer by penalizing the arclength of the ODE trajectories, but find that this fails to improve the accuracy or efficiency of the N-ODE Transformer on the challenging parity problem. We suggest future avenues of research for modifications and extensions of the N-ODE Transformer that may lead to improved accuracy and efficiency for sequence modelling tasks such as neural machine translation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge