First-order PDES for Graph Neural Networks: Advection And Burgers Equation Models
Paper and Code
Apr 03, 2024


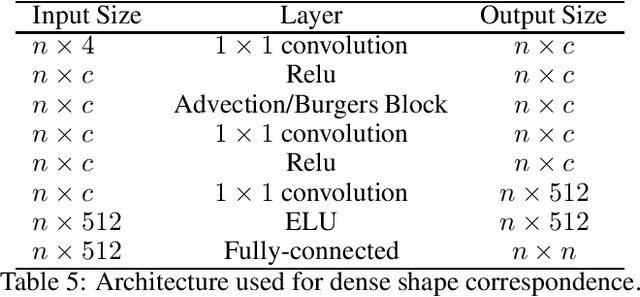
Graph Neural Networks (GNNs) have established themselves as the preferred methodology in a multitude of domains, ranging from computer vision to computational biology, especially in contexts where data inherently conform to graph structures. While many existing methods have endeavored to model GNNs using various techniques, a prevalent challenge they grapple with is the issue of over-smoothing. This paper presents new Graph Neural Network models that incorporate two first-order Partial Differential Equations (PDEs). These models do not increase complexity but effectively mitigate the over-smoothing problem. Our experimental findings highlight the capacity of our new PDE model to achieve comparable results with higher-order PDE models and fix the over-smoothing problem up to 64 layers. These results underscore the adaptability and versatility of GNNs, indicating that unconventional approaches can yield outcomes on par with established techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge