Learning Coupled System Dynamics under Incomplete Physical Constraints and Missing Data

Advances in data acquisition and computational methods have accelerated the use of differential equation based modelling for complex systems. Such systems are often described by coupled (or more) variables, yet governing equation is typically available for one variable, while the remaining variable can be accessed only through data. This mismatch between known physics and observed data poses a fundamental challenge for existing physics-informed machine learning approaches, which generally assume either complete knowledge of the governing equations or full data availability across all variables. In this paper, we introduce MUSIC (Multitask Learning Under Sparse and Incomplete Constraints), a sparsity induced multitask neural network framework that integrates partial physical constraints with data-driven learning to recover full-dimensional solutions of coupled systems when physics-constrained and data-informed variables are mutually exclusive. MUSIC employs mesh-free (random) sampling of training data and sparsity regularization, yielding highly compressed models with improved training and evaluation efficiency. We demonstrate that MUSIC accurately learns solutions (shock wave solutions, discontinuous solutions, pattern formation solutions) to complex coupled systems under data-scarce and noisy conditions, consistently outperforming non-sparse formulations. These results highlight MUSIC as a flexible and effective approach for modeling partially observed systems with incomplete physical knowledge.

Methane projections from Canada's oil sands tailings using scientific deep learning reveal significant underestimation

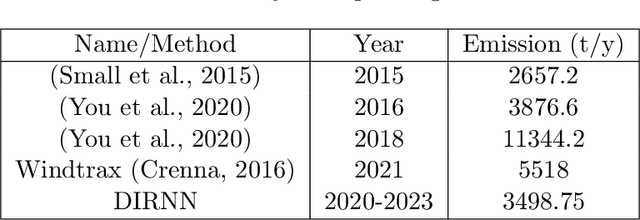
Bitumen extraction for the production of synthetic crude oil in Canada's Athabasca Oil Sands industry has recently come under spotlight for being a significant source of greenhouse gas emission. A major cause of concern is methane, a greenhouse gas produced by the anaerobic biodegradation of hydrocarbons in oil sands residues, or tailings, stored in settle basins commonly known as oil sands tailing ponds. In order to determine the methane emitting potential of these tailing ponds and have future methane projections, we use real-time weather data, mechanistic models developed from laboratory controlled experiments, and industrial reports to train a physics constrained machine learning model. Our trained model can successfully identify the directions of active ponds and estimate their emission levels, which are generally hard to obtain due to data sampling restrictions. We found that each active oil sands tailing pond could emit between 950 to 1500 tonnes of methane per year, whose environmental impact is equivalent to carbon dioxide emissions from at least 6000 gasoline powered vehicles. Although abandoned ponds are often presumed to have insignificant emissions, our findings indicate that these ponds could become active over time and potentially emit up to 1000 tonnes of methane each year. Taking an average over all datasets that was used in model training, we estimate that emissions around major oil sands regions would need to be reduced by approximately 12% over a year, to reduce the average methane concentrations to 2005 levels.

Diffusion Random Feature Model

Diffusion probabilistic models have been successfully used to generate data from noise. However, most diffusion models are computationally expensive and difficult to interpret with a lack of theoretical justification. Random feature models on the other hand have gained popularity due to their interpretability but their application to complex machine learning tasks remains limited. In this work, we present a diffusion model-inspired deep random feature model that is interpretable and gives comparable numerical results to a fully connected neural network having the same number of trainable parameters. Specifically, we extend existing results for random features and derive generalization bounds between the distribution of sampled data and the true distribution using properties of score matching. We validate our findings by generating samples on the fashion MNIST dataset and instrumental audio data.

SPADE4: Sparsity and Delay Embedding based Forecasting of Epidemics

Predicting the evolution of diseases is challenging, especially when the data availability is scarce and incomplete. The most popular tools for modelling and predicting infectious disease epidemics are compartmental models. They stratify the population into compartments according to health status and model the dynamics of these compartments using dynamical systems. However, these predefined systems may not capture the true dynamics of the epidemic due to the complexity of the disease transmission and human interactions. In order to overcome this drawback, we propose Sparsity and Delay Embedding based Forecasting (SPADE4) for predicting epidemics. SPADE4 predicts the future trajectory of an observable variable without the knowledge of the other variables or the underlying system. We use random features model with sparse regression to handle the data scarcity issue and employ Takens' delay embedding theorem to capture the nature of the underlying system from the observed variable. We show that our approach outperforms compartmental models when applied to both simulated and real data.

HARFE: Hard-Ridge Random Feature Expansion

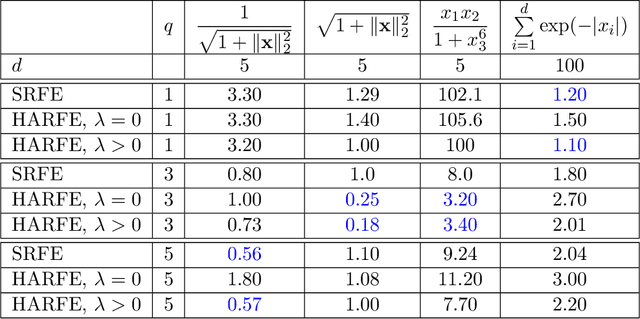
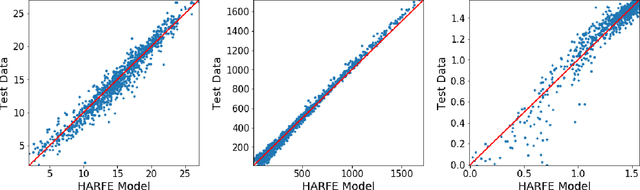
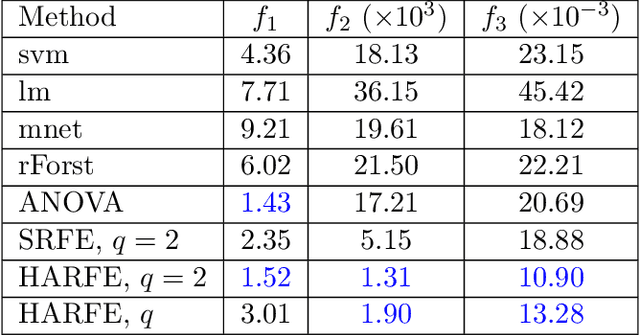
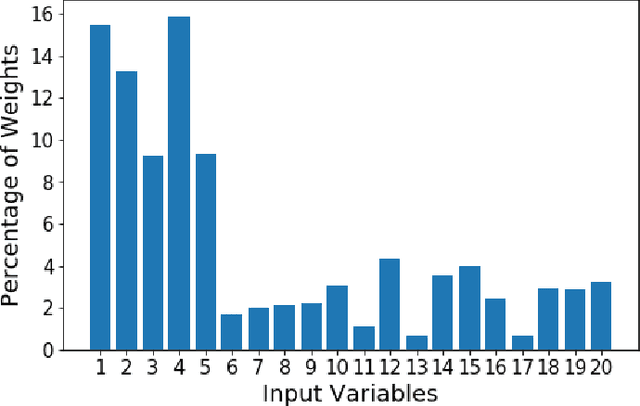
We propose a random feature model for approximating high-dimensional sparse additive functions called the hard-ridge random feature expansion method (HARFE). This method utilizes a hard-thresholding pursuit-based algorithm applied to the sparse ridge regression (SRR) problem to approximate the coefficients with respect to the random feature matrix. The SRR formulation balances between obtaining sparse models that use fewer terms in their representation and ridge-based smoothing that tend to be robust to noise and outliers. In addition, we use a random sparse connectivity pattern in the random feature matrix to match the additive function assumption. We prove that the HARFE method is guaranteed to converge with a given error bound depending on the noise and the parameters of the sparse ridge regression model. Based on numerical results on synthetic data as well as on real datasets, the HARFE approach obtains lower (or comparable) error than other state-of-the-art algorithms.