HARFE: Hard-Ridge Random Feature Expansion
Paper and Code
Feb 06, 2022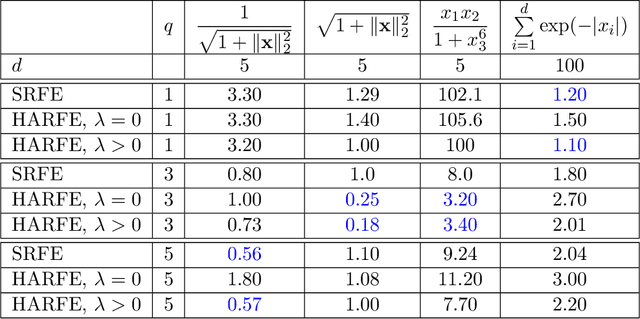
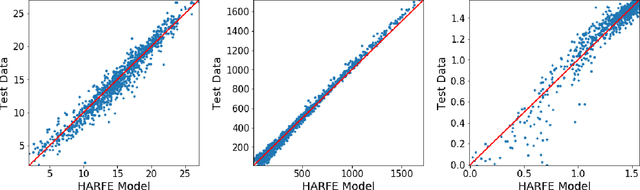
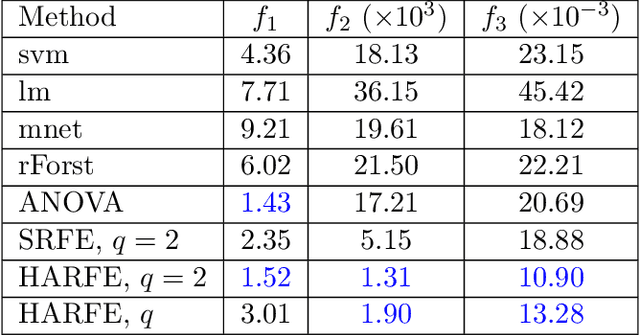
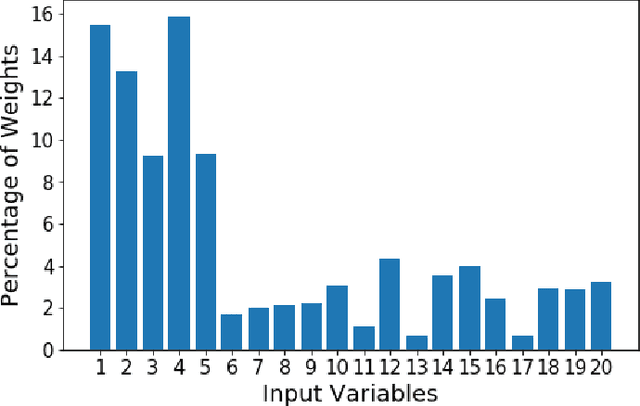
We propose a random feature model for approximating high-dimensional sparse additive functions called the hard-ridge random feature expansion method (HARFE). This method utilizes a hard-thresholding pursuit-based algorithm applied to the sparse ridge regression (SRR) problem to approximate the coefficients with respect to the random feature matrix. The SRR formulation balances between obtaining sparse models that use fewer terms in their representation and ridge-based smoothing that tend to be robust to noise and outliers. In addition, we use a random sparse connectivity pattern in the random feature matrix to match the additive function assumption. We prove that the HARFE method is guaranteed to converge with a given error bound depending on the noise and the parameters of the sparse ridge regression model. Based on numerical results on synthetic data as well as on real datasets, the HARFE approach obtains lower (or comparable) error than other state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge