Hamiltonian Monte Carlo on ReLU Neural Networks is Inefficient

We analyze the error rates of the Hamiltonian Monte Carlo algorithm with leapfrog integrator for Bayesian neural network inference. We show that due to the non-differentiability of activation functions in the ReLU family, leapfrog HMC for networks with these activation functions has a large local error rate of $\Omega(\epsilon)$ rather than the classical error rate of $O(\epsilon^3)$. This leads to a higher rejection rate of the proposals, making the method inefficient. We then verify our theoretical findings through empirical simulations as well as experiments on a real-world dataset that highlight the inefficiency of HMC inference on ReLU-based neural networks compared to analytical networks.

Simple Transferability Estimation for Regression Tasks

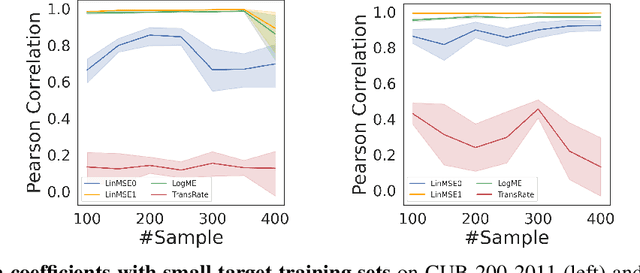
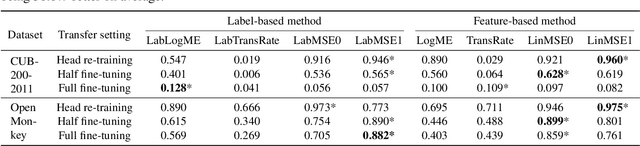
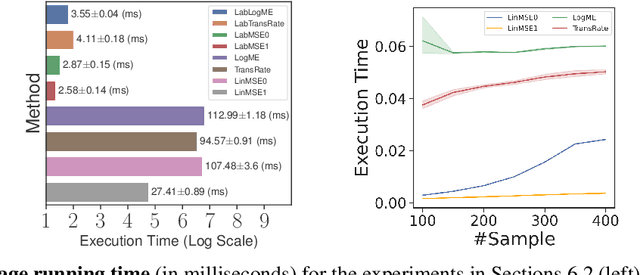
We consider transferability estimation, the problem of estimating how well deep learning models transfer from a source to a target task. We focus on regression tasks, which received little previous attention, and propose two simple and computationally efficient approaches that estimate transferability based on the negative regularized mean squared error of a linear regression model. We prove novel theoretical results connecting our approaches to the actual transferability of the optimal target models obtained from the transfer learning process. Despite their simplicity, our approaches significantly outperform existing state-of-the-art regression transferability estimators in both accuracy and efficiency. On two large-scale keypoint regression benchmarks, our approaches yield 12% to 36% better results on average while being at least 27% faster than previous state-of-the-art methods.

A Generalization Bound of Deep Neural Networks for Dependent Data

Existing generalization bounds for deep neural networks require data to be independent and identically distributed (iid). This assumption may not hold in real-life applications such as evolutionary biology, infectious disease epidemiology, and stock price prediction. This work establishes a generalization bound of feed-forward neural networks for non-stationary $\phi$-mixing data.

SPADE4: Sparsity and Delay Embedding based Forecasting of Epidemics

Predicting the evolution of diseases is challenging, especially when the data availability is scarce and incomplete. The most popular tools for modelling and predicting infectious disease epidemics are compartmental models. They stratify the population into compartments according to health status and model the dynamics of these compartments using dynamical systems. However, these predefined systems may not capture the true dynamics of the epidemic due to the complexity of the disease transmission and human interactions. In order to overcome this drawback, we propose Sparsity and Delay Embedding based Forecasting (SPADE4) for predicting epidemics. SPADE4 predicts the future trajectory of an observable variable without the knowledge of the other variables or the underlying system. We use random features model with sparse regression to handle the data scarcity issue and employ Takens' delay embedding theorem to capture the nature of the underlying system from the observed variable. We show that our approach outperforms compartmental models when applied to both simulated and real data.

Generalization Bounds for Deep Transfer Learning Using Majority Predictor Accuracy

We analyze new generalization bounds for deep learning models trained by transfer learning from a source to a target task. Our bounds utilize a quantity called the majority predictor accuracy, which can be computed efficiently from data. We show that our theory is useful in practice since it implies that the majority predictor accuracy can be used as a transferability measure, a fact that is also validated by our experiments.

Posterior concentration and fast convergence rates for generalized Bayesian learning

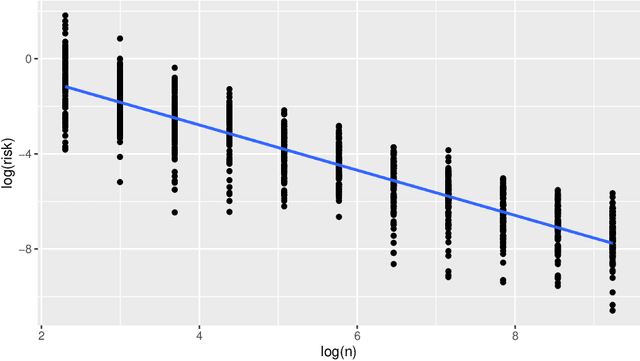
In this paper, we study the learning rate of generalized Bayes estimators in a general setting where the hypothesis class can be uncountable and have an irregular shape, the loss function can have heavy tails, and the optimal hypothesis may not be unique. We prove that under the multi-scale Bernstein's condition, the generalized posterior distribution concentrates around the set of optimal hypotheses and the generalized Bayes estimator can achieve fast learning rate. Our results are applied to show that the standard Bayesian linear regression is robust to heavy-tailed distributions.

Searching for Minimal Optimal Neural Networks

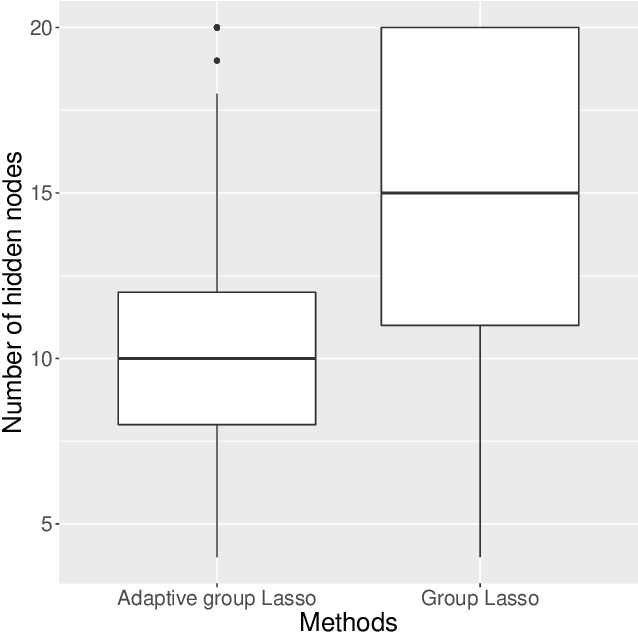
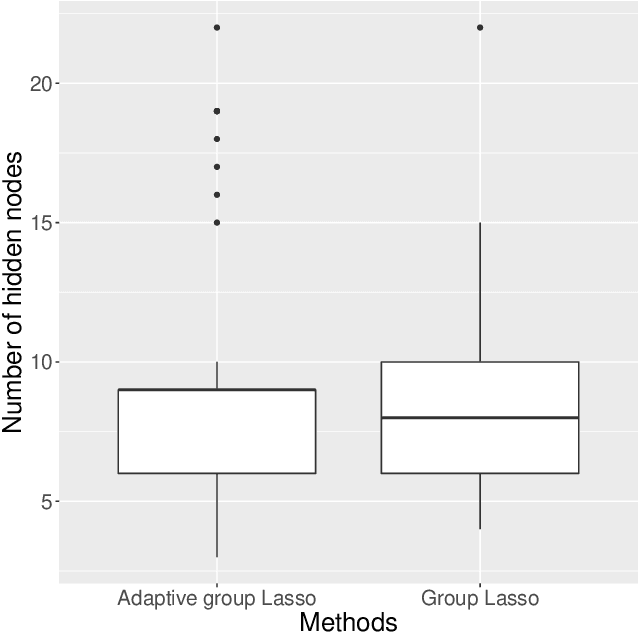
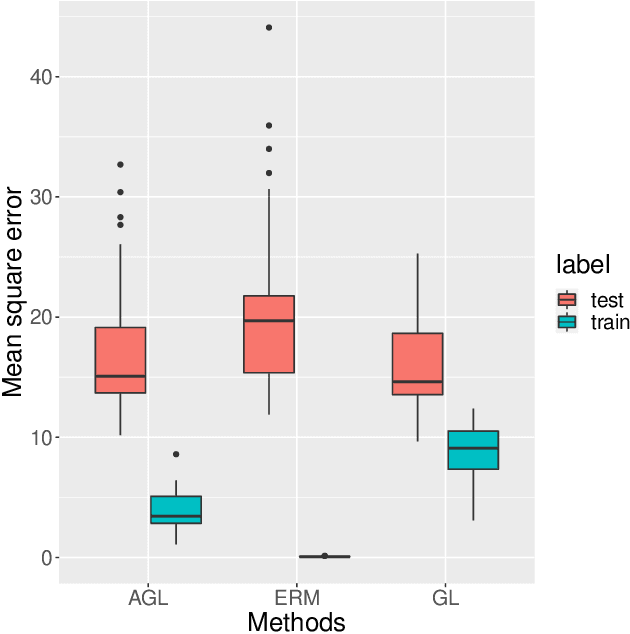
Large neural network models have high predictive power but may suffer from overfitting if the training set is not large enough. Therefore, it is desirable to select an appropriate size for neural networks. The destructive approach, which starts with a large architecture and then reduces the size using a Lasso-type penalty, has been used extensively for this task. Despite its popularity, there is no theoretical guarantee for this technique. Based on the notion of minimal neural networks, we posit a rigorous mathematical framework for studying the asymptotic theory of the destructive technique. We prove that Adaptive group Lasso is consistent and can reconstruct the correct number of hidden nodes of one-hidden-layer feedforward networks with high probability. To the best of our knowledge, this is the first theoretical result establishing for the destructive technique.

Adaptive Group Lasso Neural Network Models for Functions of Few Variables and Time-Dependent Data

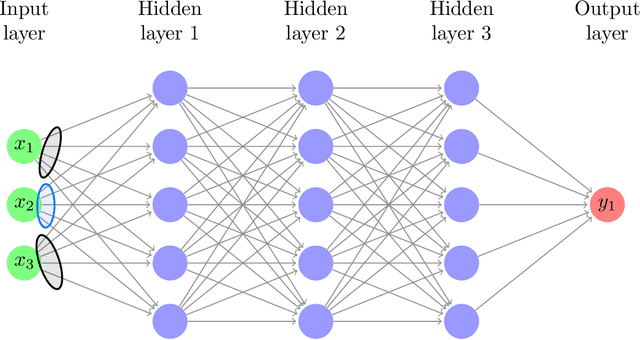
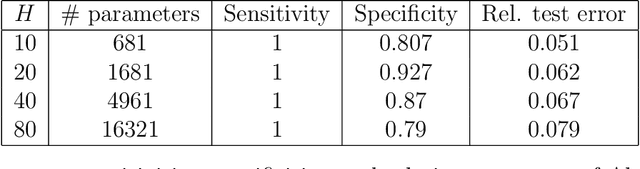
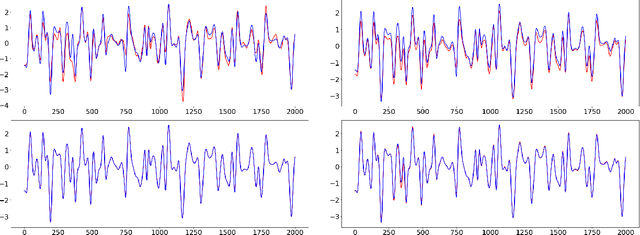
In this paper, we propose an adaptive group Lasso deep neural network for high-dimensional function approximation where input data are generated from a dynamical system and the target function depends on few active variables or few linear combinations of variables. We approximate the target function by a deep neural network and enforce an adaptive group Lasso constraint to the weights of a suitable hidden layer in order to represent the constraint on the target function. Our empirical studies show that the proposed method outperforms recent state-of-the-art methods including the sparse dictionary matrix method, neural networks with or without group Lasso penalty.

OASIS: An Active Framework for Set Inversion

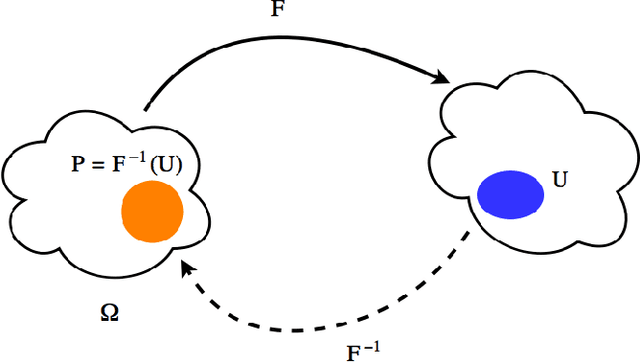
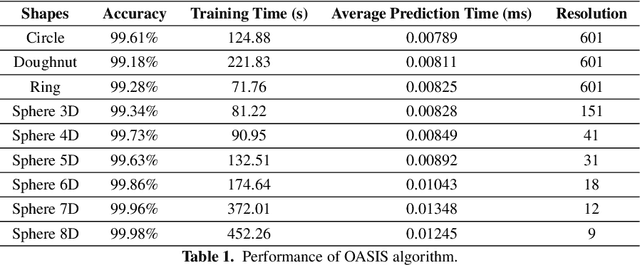
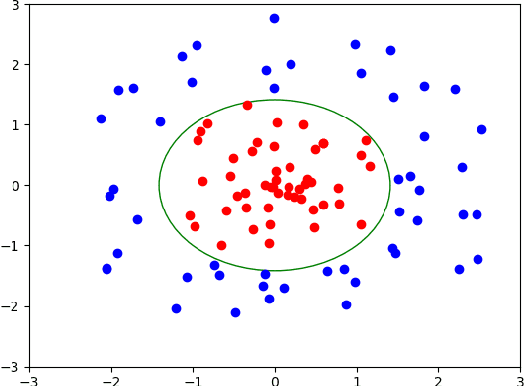
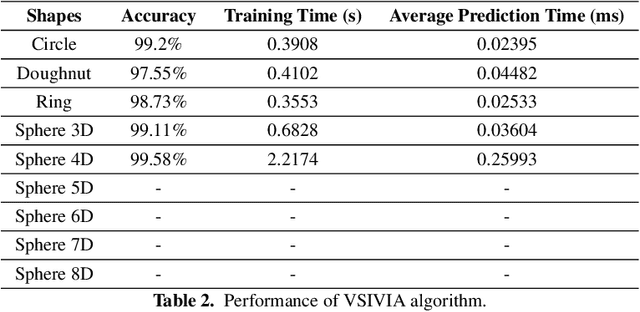
In this work, we introduce a novel method for solving the set inversion problem by formulating it as a binary classification problem. Aiming to develop a fast algorithm that can work effectively with high-dimensional and computationally expensive nonlinear models, we focus on active learning, a family of new and powerful techniques which can achieve the same level of accuracy with fewer data points compared to traditional learning methods. Specifically, we propose OASIS, an active learning framework using Support Vector Machine algorithms for solving the problem of set inversion. Our method works well in high dimensions and its computational cost is relatively robust to the increase of dimension. We illustrate the performance of OASIS by several simulation studies and show that our algorithm outperforms VISIA, the state-of-the-art method.

Consistent Feature Selection for Analytic Deep Neural Networks

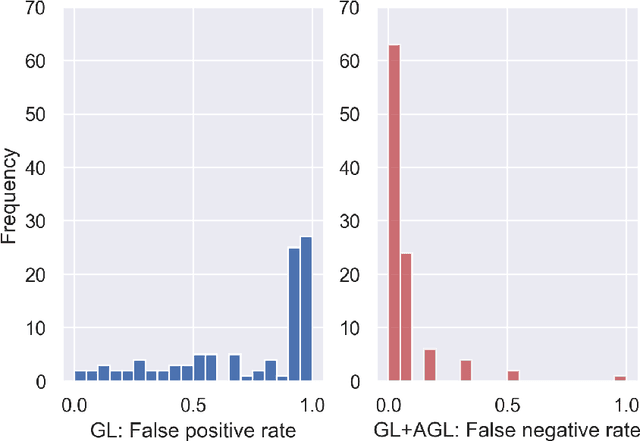
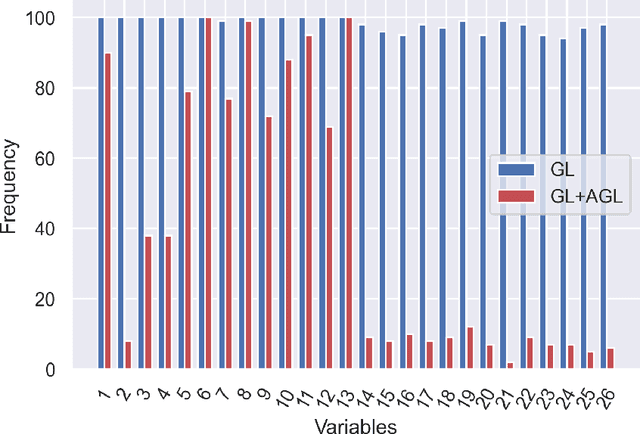
One of the most important steps toward interpretability and explainability of neural network models is feature selection, which aims to identify the subset of relevant features. Theoretical results in the field have mostly focused on the prediction aspect of the problem with virtually no work on feature selection consistency for deep neural networks due to the model's severe nonlinearity and unidentifiability. This lack of theoretical foundation casts doubt on the applicability of deep learning to contexts where correct interpretations of the features play a central role. In this work, we investigate the problem of feature selection for analytic deep networks. We prove that for a wide class of networks, including deep feed-forward neural networks, convolutional neural networks, and a major sub-class of residual neural networks, the Adaptive Group Lasso selection procedure with Group Lasso as the base estimator is selection-consistent. The work provides further evidence that Group Lasso might be inefficient for feature selection with neural networks and advocates the use of Adaptive Group Lasso over the popular Group Lasso.