Searching for Minimal Optimal Neural Networks
Paper and Code
Sep 27, 2021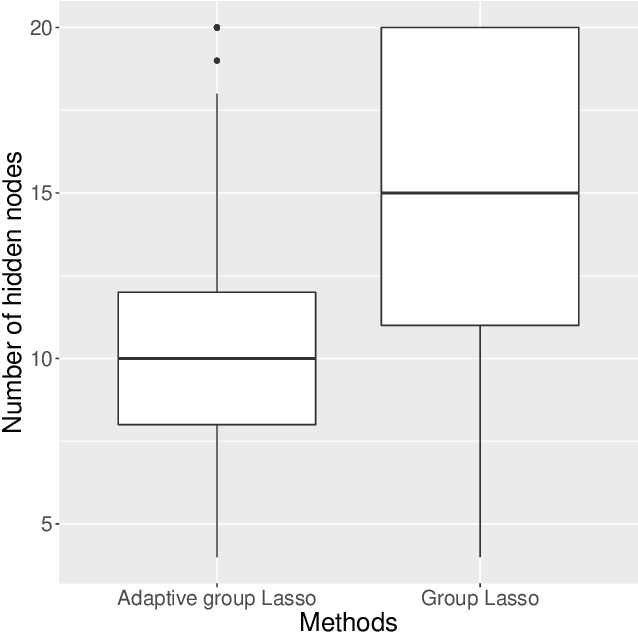
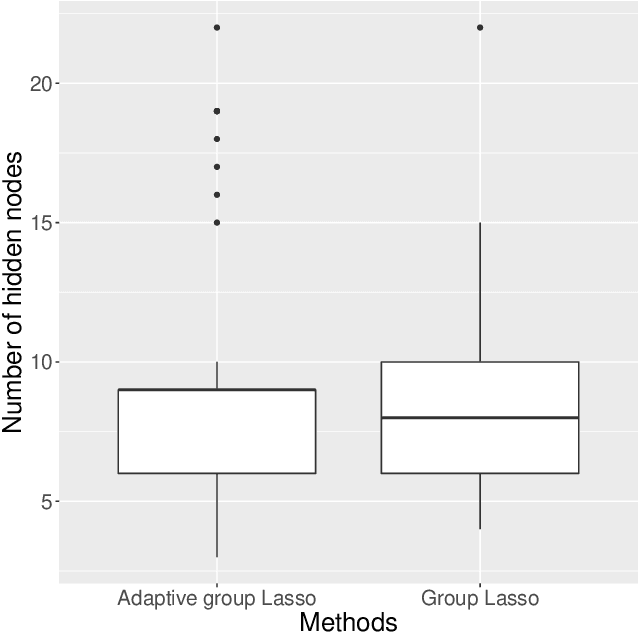
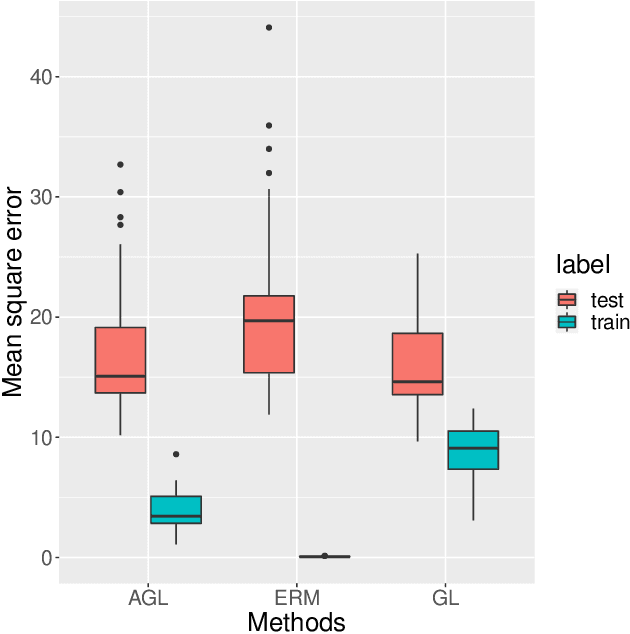
Large neural network models have high predictive power but may suffer from overfitting if the training set is not large enough. Therefore, it is desirable to select an appropriate size for neural networks. The destructive approach, which starts with a large architecture and then reduces the size using a Lasso-type penalty, has been used extensively for this task. Despite its popularity, there is no theoretical guarantee for this technique. Based on the notion of minimal neural networks, we posit a rigorous mathematical framework for studying the asymptotic theory of the destructive technique. We prove that Adaptive group Lasso is consistent and can reconstruct the correct number of hidden nodes of one-hidden-layer feedforward networks with high probability. To the best of our knowledge, this is the first theoretical result establishing for the destructive technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge