Posterior concentration and fast convergence rates for generalized Bayesian learning
Paper and Code
Nov 19, 2021
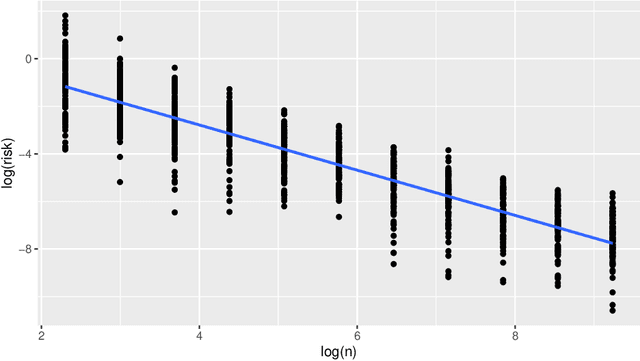
In this paper, we study the learning rate of generalized Bayes estimators in a general setting where the hypothesis class can be uncountable and have an irregular shape, the loss function can have heavy tails, and the optimal hypothesis may not be unique. We prove that under the multi-scale Bernstein's condition, the generalized posterior distribution concentrates around the set of optimal hypotheses and the generalized Bayes estimator can achieve fast learning rate. Our results are applied to show that the standard Bayesian linear regression is robust to heavy-tailed distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge