Neural Shortest Path for Surface Reconstruction from Point Clouds

In this paper, we propose the neural shortest path (NSP), a vector-valued implicit neural representation (INR) that approximates a distance function and its gradient. The key feature of NSP is to learn the exact shortest path (ESP), which directs an arbitrary point to its nearest point on the target surface. The NSP is decomposed into its magnitude and direction, and a variable splitting method is used that each decomposed component approximates a distance function and its gradient, respectively. Unlike to existing methods of learning the distance function itself, the NSP ensures the simultaneous recovery of the distance function and its gradient. We mathematically prove that the decomposed representation of NSP guarantees the convergence of the magnitude of NSP in the $H^1$ norm. Furthermore, we devise a novel loss function that enforces the property of ESP, demonstrating that its global minimum is the ESP. We evaluate the performance of the NSP through comprehensive experiments on diverse datasets, validating its capacity to reconstruct high-quality surfaces with the robustness to noise and data sparsity. The numerical results show substantial improvements over state-of-the-art methods, highlighting the importance of learning the ESP, the product of distance function and its gradient, for representing a wide variety of complex surfaces.

Neural Implicit Solution Formula for Efficiently Solving Hamilton-Jacobi Equations

This paper presents an implicit solution formula for the Hamilton-Jacobi partial differential equation (HJ PDE). The formula is derived using the method of characteristics and is shown to coincide with the Hopf and Lax formulas in the case where either the Hamiltonian or the initial function is convex. It provides a simple and efficient numerical approach for computing the viscosity solution of HJ PDEs, bypassing the need for the Legendre transform of the Hamiltonian or the initial condition, and the explicit computation of individual characteristic trajectories. A deep learning-based methodology is proposed to learn this implicit solution formula, leveraging the mesh-free nature of deep learning to ensure scalability for high-dimensional problems. Building upon this framework, an algorithm is developed that approximates the characteristic curves piecewise linearly for state-dependent Hamiltonians. Extensive experimental results demonstrate that the proposed method delivers highly accurate solutions, even for nonconvex Hamiltonians, and exhibits remarkable scalability, achieving computational efficiency for problems up to 40 dimensions.

Beyond Derivative Pathology of PINNs: Variable Splitting Strategy with Convergence Analysis

Physics-informed neural networks (PINNs) have recently emerged as effective methods for solving partial differential equations (PDEs) in various problems. Substantial research focuses on the failure modes of PINNs due to their frequent inaccuracies in predictions. However, most are based on the premise that minimizing the loss function to zero causes the network to converge to a solution of the governing PDE. In this study, we prove that PINNs encounter a fundamental issue that the premise is invalid. We also reveal that this issue stems from the inability to regulate the behavior of the derivatives of the predicted solution. Inspired by the \textit{derivative pathology} of PINNs, we propose a \textit{variable splitting} strategy that addresses this issue by parameterizing the gradient of the solution as an auxiliary variable. We demonstrate that using the auxiliary variable eludes derivative pathology by enabling direct monitoring and regulation of the gradient of the predicted solution. Moreover, we prove that the proposed method guarantees convergence to a generalized solution for second-order linear PDEs, indicating its applicability to various problems.

$p$-Poisson surface reconstruction in curl-free flow from point clouds

The aim of this paper is the reconstruction of a smooth surface from an unorganized point cloud sampled by a closed surface, with the preservation of geometric shapes, without any further information other than the point cloud. Implicit neural representations (INRs) have recently emerged as a promising approach to surface reconstruction. However, the reconstruction quality of existing methods relies on ground truth implicit function values or surface normal vectors. In this paper, we show that proper supervision of partial differential equations and fundamental properties of differential vector fields are sufficient to robustly reconstruct high-quality surfaces. We cast the $p$-Poisson equation to learn a signed distance function (SDF) and the reconstructed surface is implicitly represented by the zero-level set of the SDF. For efficient training, we develop a variable splitting structure by introducing a gradient of the SDF as an auxiliary variable and impose the $p$-Poisson equation directly on the auxiliary variable as a hard constraint. Based on the curl-free property of the gradient field, we impose a curl-free constraint on the auxiliary variable, which leads to a more faithful reconstruction. Experiments on standard benchmark datasets show that the proposed INR provides a superior and robust reconstruction. The code is available at \url{https://github.com/Yebbi/PINC}.

Restoration based Generative Models

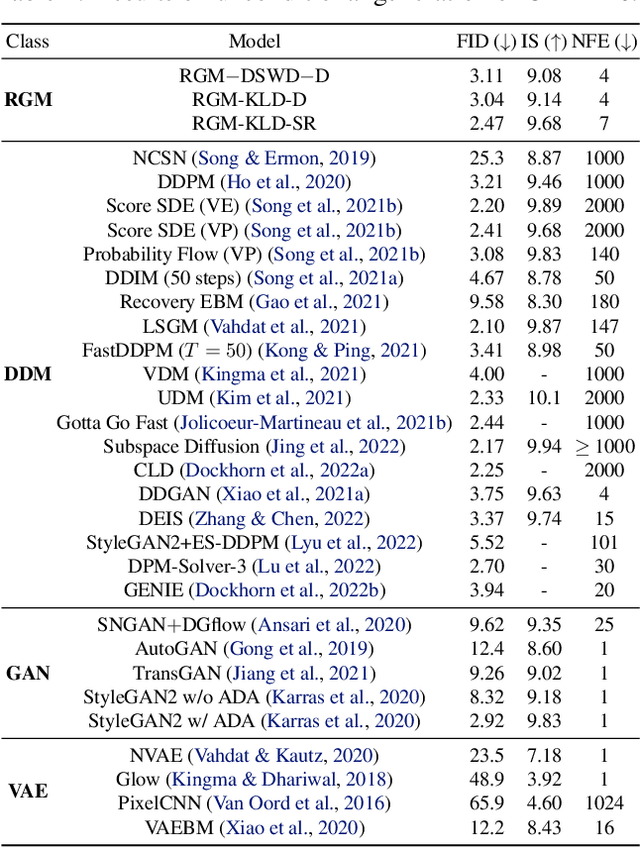
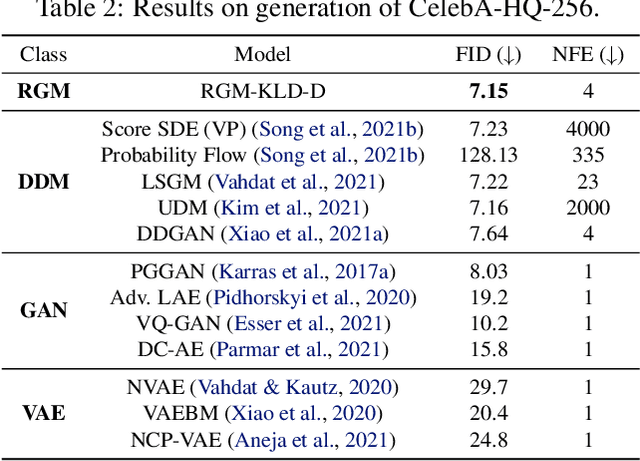
Denoising diffusion models (DDMs) have recently attracted increasing attention by showing impressive synthesis quality. DDMs are built on a diffusion process that pushes data to the noise distribution and the models learn to denoise. In this paper, we establish the interpretation of DDMs in terms of image restoration (IR). Integrating IR literature allows us to use an alternative objective and diverse forward processes, not confining to the diffusion process. By imposing prior knowledge on the loss function grounded on MAP-based estimation, we eliminate the need for the expensive sampling of DDMs. Also, we propose a multi-scale training, which improves the performance compared to the diffusion process, by taking advantage of the flexibility of the forward process. Experimental results demonstrate that our model improves the quality and efficiency of both training and inference. Furthermore, we show the applicability of our model to inverse problems. We believe that our framework paves the way for designing a new type of flexible general generative model.

Learning PDE Solution Operator for Continuous Modeling of Time-Series

Learning underlying dynamics from data is important and challenging in many real-world scenarios. Incorporating differential equations (DEs) to design continuous networks has drawn much attention recently, however, most prior works make specific assumptions on the type of DEs, making the model specialized for particular problems. This work presents a partial differential equation (PDE) based framework which improves the dynamics modeling capability. Building upon the recent Fourier neural operator, we propose a neural operator that can handle time continuously without requiring iterative operations or specific grids of temporal discretization. A theoretical result demonstrating its universality is provided. We also uncover an intrinsic property of neural operators that improves data efficiency and model generalization by ensuring stability. Our model achieves superior accuracy in dealing with time-dependent PDEs compared to existing models. Furthermore, several numerical pieces of evidence validate that our method better represents a wide range of dynamics and outperforms state-of-the-art DE-based models in real-time-series applications. Our framework opens up a new way for a continuous representation of neural networks that can be readily adopted for real-world applications.