Myungjoo Kang
Leveraging Prior Knowledge of Diffusion Model for Person Search
Oct 02, 2025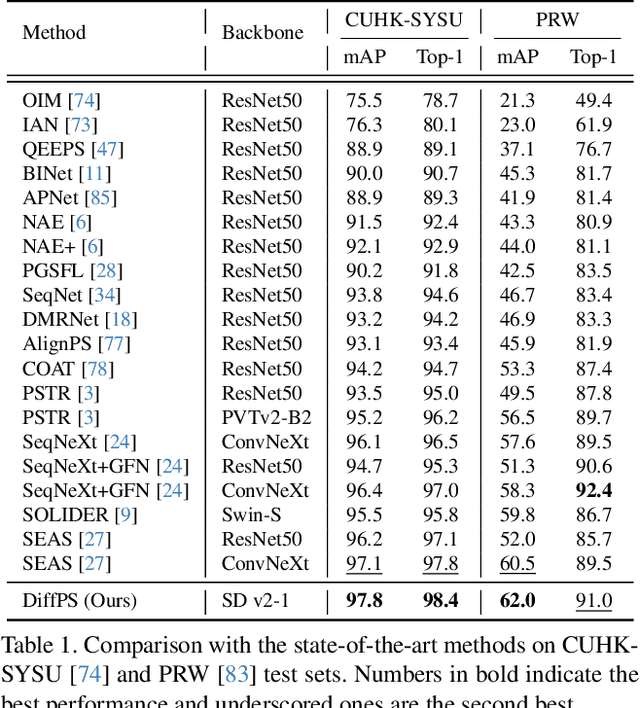

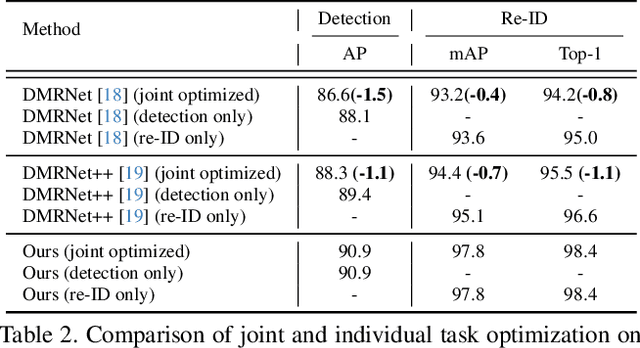

Abstract:Person search aims to jointly perform person detection and re-identification by localizing and identifying a query person within a gallery of uncropped scene images. Existing methods predominantly utilize ImageNet pre-trained backbones, which may be suboptimal for capturing the complex spatial context and fine-grained identity cues necessary for person search. Moreover, they rely on a shared backbone feature for both person detection and re-identification, leading to suboptimal features due to conflicting optimization objectives. In this paper, we propose DiffPS (Diffusion Prior Knowledge for Person Search), a novel framework that leverages a pre-trained diffusion model while eliminating the optimization conflict between two sub-tasks. We analyze key properties of diffusion priors and propose three specialized modules: (i) Diffusion-Guided Region Proposal Network (DGRPN) for enhanced person localization, (ii) Multi-Scale Frequency Refinement Network (MSFRN) to mitigate shape bias, and (iii) Semantic-Adaptive Feature Aggregation Network (SFAN) to leverage text-aligned diffusion features. DiffPS sets a new state-of-the-art on CUHK-SYSU and PRW.
MINR: Implicit Neural Representations with Masked Image Modelling
Jul 30, 2025Abstract:Self-supervised learning methods like masked autoencoders (MAE) have shown significant promise in learning robust feature representations, particularly in image reconstruction-based pretraining task. However, their performance is often strongly dependent on the masking strategies used during training and can degrade when applied to out-of-distribution data. To address these limitations, we introduce the masked implicit neural representations (MINR) framework that synergizes implicit neural representations with masked image modeling. MINR learns a continuous function to represent images, enabling more robust and generalizable reconstructions irrespective of masking strategies. Our experiments demonstrate that MINR not only outperforms MAE in in-domain scenarios but also in out-of-distribution settings, while reducing model complexity. The versatility of MINR extends to various self-supervised learning applications, confirming its utility as a robust and efficient alternative to existing frameworks.
Divergence-Based Similarity Function for Multi-View Contrastive Learning
Jul 09, 2025Abstract:Recent success in contrastive learning has sparked growing interest in more effectively leveraging multiple augmented views of an instance. While prior methods incorporate multiple views at the loss or feature level, they primarily capture pairwise relationships and fail to model the joint structure across all views. In this work, we propose a divergence-based similarity function (DSF) that explicitly captures the joint structure by representing each set of augmented views as a distribution and measuring similarity as the divergence between distributions. Extensive experiments demonstrate that DSF consistently improves performance across various tasks, including kNN classification and linear evaluation, while also offering greater efficiency compared to other multi-view methods. Furthermore, we establish a theoretical connection between DSF and cosine similarity, and show that, unlike cosine similarity, DSF operates effectively without requiring a temperature hyperparameter.
Neural Shortest Path for Surface Reconstruction from Point Clouds
Feb 09, 2025Abstract:In this paper, we propose the neural shortest path (NSP), a vector-valued implicit neural representation (INR) that approximates a distance function and its gradient. The key feature of NSP is to learn the exact shortest path (ESP), which directs an arbitrary point to its nearest point on the target surface. The NSP is decomposed into its magnitude and direction, and a variable splitting method is used that each decomposed component approximates a distance function and its gradient, respectively. Unlike to existing methods of learning the distance function itself, the NSP ensures the simultaneous recovery of the distance function and its gradient. We mathematically prove that the decomposed representation of NSP guarantees the convergence of the magnitude of NSP in the $H^1$ norm. Furthermore, we devise a novel loss function that enforces the property of ESP, demonstrating that its global minimum is the ESP. We evaluate the performance of the NSP through comprehensive experiments on diverse datasets, validating its capacity to reconstruct high-quality surfaces with the robustness to noise and data sparsity. The numerical results show substantial improvements over state-of-the-art methods, highlighting the importance of learning the ESP, the product of distance function and its gradient, for representing a wide variety of complex surfaces.
MMVA: Multimodal Matching Based on Valence and Arousal across Images, Music, and Musical Captions
Jan 02, 2025



Abstract:We introduce Multimodal Matching based on Valence and Arousal (MMVA), a tri-modal encoder framework designed to capture emotional content across images, music, and musical captions. To support this framework, we expand the Image-Music-Emotion-Matching-Net (IMEMNet) dataset, creating IMEMNet-C which includes 24,756 images and 25,944 music clips with corresponding musical captions. We employ multimodal matching scores based on the continuous valence (emotional positivity) and arousal (emotional intensity) values. This continuous matching score allows for random sampling of image-music pairs during training by computing similarity scores from the valence-arousal values across different modalities. Consequently, the proposed approach achieves state-of-the-art performance in valence-arousal prediction tasks. Furthermore, the framework demonstrates its efficacy in various zeroshot tasks, highlighting the potential of valence and arousal predictions in downstream applications.
Beyond Derivative Pathology of PINNs: Variable Splitting Strategy with Convergence Analysis
Sep 30, 2024Abstract:Physics-informed neural networks (PINNs) have recently emerged as effective methods for solving partial differential equations (PDEs) in various problems. Substantial research focuses on the failure modes of PINNs due to their frequent inaccuracies in predictions. However, most are based on the premise that minimizing the loss function to zero causes the network to converge to a solution of the governing PDE. In this study, we prove that PINNs encounter a fundamental issue that the premise is invalid. We also reveal that this issue stems from the inability to regulate the behavior of the derivatives of the predicted solution. Inspired by the \textit{derivative pathology} of PINNs, we propose a \textit{variable splitting} strategy that addresses this issue by parameterizing the gradient of the solution as an auxiliary variable. We demonstrate that using the auxiliary variable eludes derivative pathology by enabling direct monitoring and regulation of the gradient of the predicted solution. Moreover, we prove that the proposed method guarantees convergence to a generalized solution for second-order linear PDEs, indicating its applicability to various problems.
Why Rectified Power Unit Networks Fail and How to Improve It: An Effective Theory Perspective
Aug 04, 2024
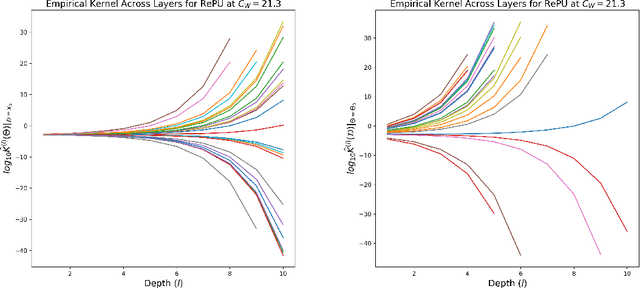
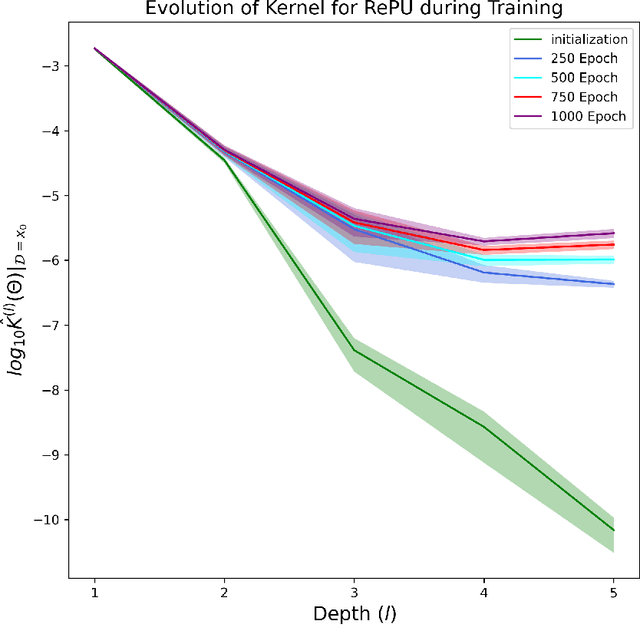
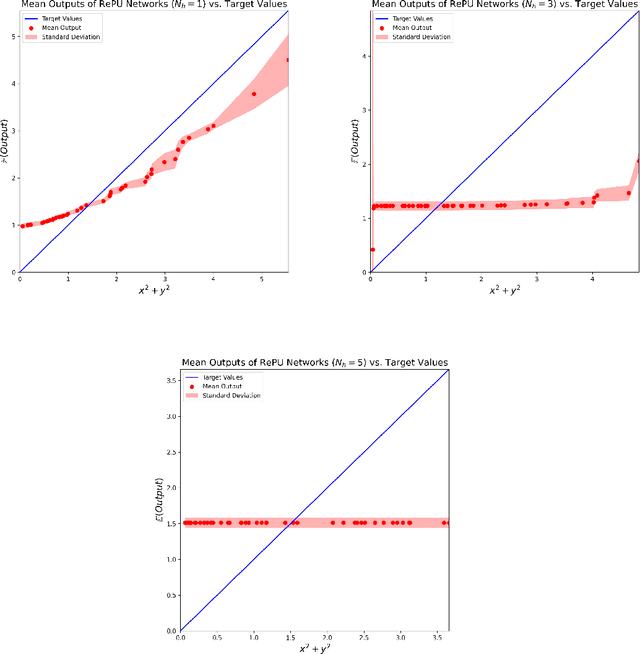
Abstract:The Rectified Power Unit (RePU) activation functions, unlike the Rectified Linear Unit (ReLU), have the advantage of being a differentiable function when constructing neural networks. However, it can be experimentally observed when deep layers are stacked, neural networks constructed with RePU encounter critical issues. These issues include the values exploding or vanishing and failure of training. And these happen regardless of the hyperparameter initialization. From the perspective of effective theory, we aim to identify the causes of this phenomenon and propose a new activation function that retains the advantages of RePU while overcoming its drawbacks.
FLEUR: An Explainable Reference-Free Evaluation Metric for Image Captioning Using a Large Multimodal Model
Jun 10, 2024
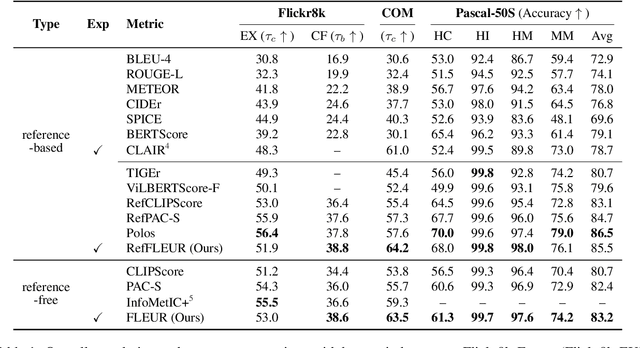
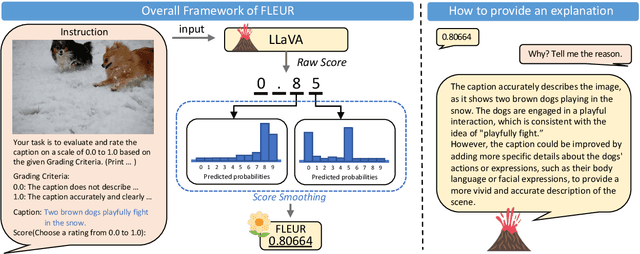
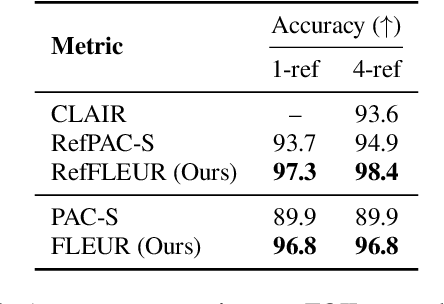
Abstract:Most existing image captioning evaluation metrics focus on assigning a single numerical score to a caption by comparing it with reference captions. However, these methods do not provide an explanation for the assigned score. Moreover, reference captions are expensive to acquire. In this paper, we propose FLEUR, an explainable reference-free metric to introduce explainability into image captioning evaluation metrics. By leveraging a large multimodal model, FLEUR can evaluate the caption against the image without the need for reference captions, and provide the explanation for the assigned score. We introduce score smoothing to align as closely as possible with human judgment and to be robust to user-defined grading criteria. FLEUR achieves high correlations with human judgment across various image captioning evaluation benchmarks and reaches state-of-the-art results on Flickr8k-CF, COMPOSITE, and Pascal-50S within the domain of reference-free evaluation metrics. Our source code and results are publicly available at: https://github.com/Yebin46/FLEUR.
Neural Operators Learn the Local Physics of Magnetohydrodynamics
Apr 24, 2024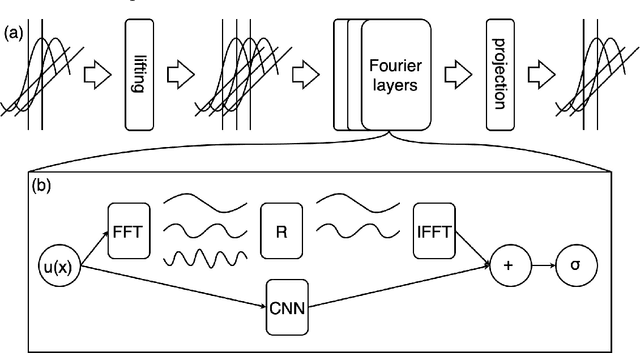
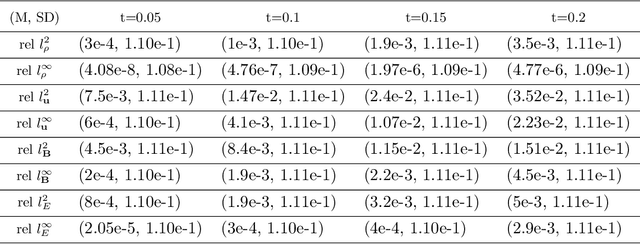
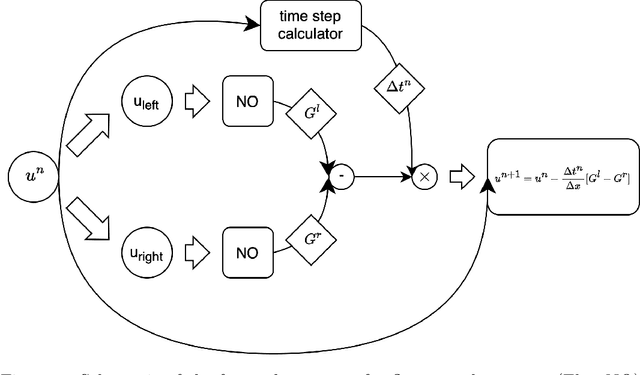
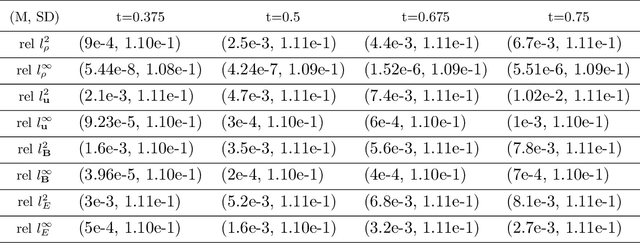
Abstract:Magnetohydrodynamics (MHD) plays a pivotal role in describing the dynamics of plasma and conductive fluids, essential for understanding phenomena such as the structure and evolution of stars and galaxies, and in nuclear fusion for plasma motion through ideal MHD equations. Solving these hyperbolic PDEs requires sophisticated numerical methods, presenting computational challenges due to complex structures and high costs. Recent advances introduce neural operators like the Fourier Neural Operator (FNO) as surrogate models for traditional numerical analyses. This study explores a modified Flux Fourier neural operator model to approximate the numerical flux of ideal MHD, offering a novel approach that outperforms existing neural operator models by enabling continuous inference, generalization outside sampled distributions, and faster computation compared to classical numerical schemes.
Revealing and Utilizing In-group Favoritism for Graph-based Collaborative Filtering
Apr 23, 2024



Abstract:When it comes to a personalized item recommendation system, It is essential to extract users' preferences and purchasing patterns. Assuming that users in the real world form a cluster and there is common favoritism in each cluster, in this work, we introduce Co-Clustering Wrapper (CCW). We compute co-clusters of users and items with co-clustering algorithms and add CF subnetworks for each cluster to extract the in-group favoritism. Combining the features from the networks, we obtain rich and unified information about users. We experimented real world datasets considering two aspects: Finding the number of groups divided according to in-group preference, and measuring the quantity of improvement of the performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge