Youngsoo Ha
Neural Operators Learn the Local Physics of Magnetohydrodynamics
Apr 24, 2024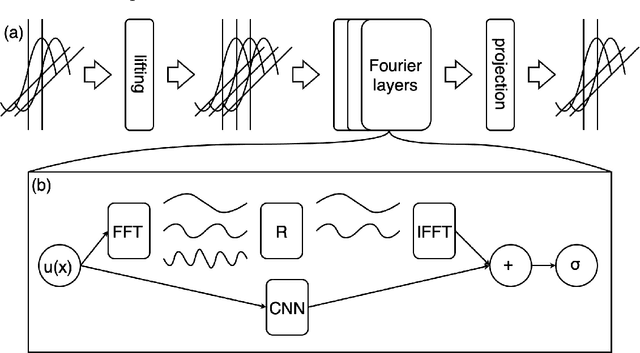
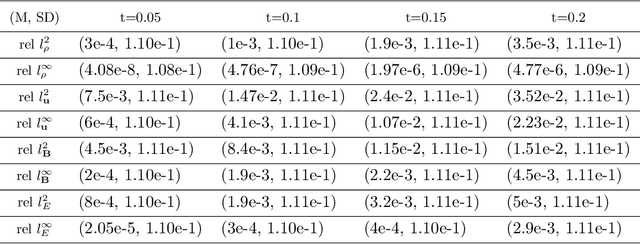
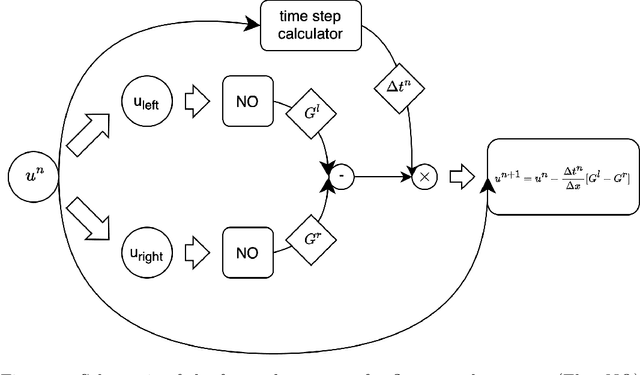
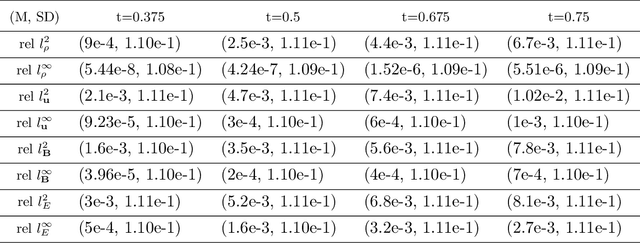
Abstract:Magnetohydrodynamics (MHD) plays a pivotal role in describing the dynamics of plasma and conductive fluids, essential for understanding phenomena such as the structure and evolution of stars and galaxies, and in nuclear fusion for plasma motion through ideal MHD equations. Solving these hyperbolic PDEs requires sophisticated numerical methods, presenting computational challenges due to complex structures and high costs. Recent advances introduce neural operators like the Fourier Neural Operator (FNO) as surrogate models for traditional numerical analyses. This study explores a modified Flux Fourier neural operator model to approximate the numerical flux of ideal MHD, offering a novel approach that outperforms existing neural operator models by enabling continuous inference, generalization outside sampled distributions, and faster computation compared to classical numerical schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge