Learning PDE Solution Operator for Continuous Modeling of Time-Series

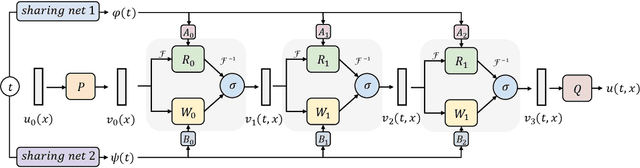
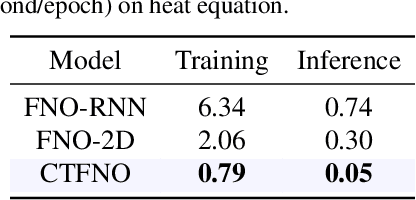
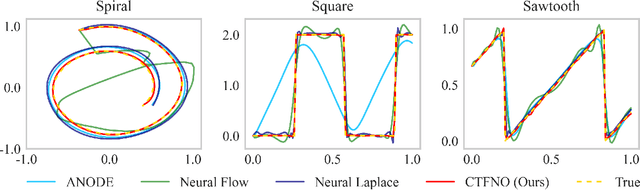
Learning underlying dynamics from data is important and challenging in many real-world scenarios. Incorporating differential equations (DEs) to design continuous networks has drawn much attention recently, however, most prior works make specific assumptions on the type of DEs, making the model specialized for particular problems. This work presents a partial differential equation (PDE) based framework which improves the dynamics modeling capability. Building upon the recent Fourier neural operator, we propose a neural operator that can handle time continuously without requiring iterative operations or specific grids of temporal discretization. A theoretical result demonstrating its universality is provided. We also uncover an intrinsic property of neural operators that improves data efficiency and model generalization by ensuring stability. Our model achieves superior accuracy in dealing with time-dependent PDEs compared to existing models. Furthermore, several numerical pieces of evidence validate that our method better represents a wide range of dynamics and outperforms state-of-the-art DE-based models in real-time-series applications. Our framework opens up a new way for a continuous representation of neural networks that can be readily adopted for real-world applications.

Minimal Width for Universal Property of Deep RNN

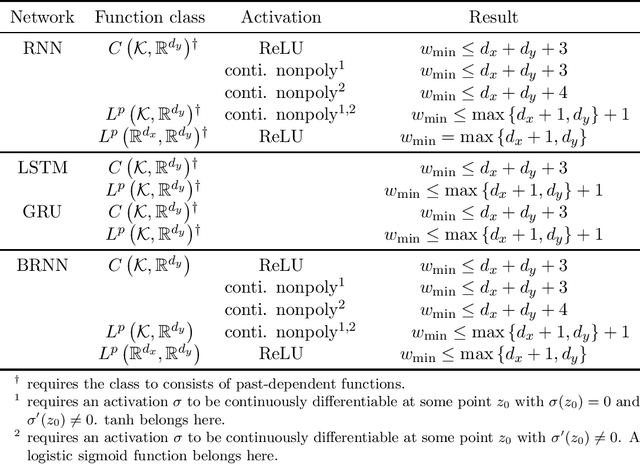
A recurrent neural network (RNN) is a widely used deep-learning network for dealing with sequential data. Imitating a dynamical system, an infinite-width RNN can approximate any open dynamical system in a compact domain. In general, deep networks with bounded widths are more effective than wide networks in practice; however, the universal approximation theorem for deep narrow structures has yet to be extensively studied. In this study, we prove the universality of deep narrow RNNs and show that the upper bound of the minimum width for universality can be independent of the length of the data. Specifically, we show that a deep RNN with ReLU activation can approximate any continuous function or $L^p$ function with the widths $d_x+d_y+2$ and $\max\{d_x+1,d_y\}$, respectively, where the target function maps a finite sequence of vectors in $\mathbb{R}^{d_x}$ to a finite sequence of vectors in $\mathbb{R}^{d_y}$. We also compute the additional width required if the activation function is $\tanh$ or more. In addition, we prove the universality of other recurrent networks, such as bidirectional RNNs. Bridging a multi-layer perceptron and an RNN, our theory and proof technique can be an initial step toward further research on deep RNNs.