On Expressive Power of Quantized Neural Networks under Fixed-Point Arithmetic

Research into the expressive power of neural networks typically considers real parameters and operations without rounding error. In this work, we study universal approximation property of quantized networks under discrete fixed-point parameters and fixed-point operations that may incur errors due to rounding. We first provide a necessary condition and a sufficient condition on fixed-point arithmetic and activation functions for universal approximation of quantized networks. Then, we show that various popular activation functions satisfy our sufficient condition, e.g., Sigmoid, ReLU, ELU, SoftPlus, SiLU, Mish, and GELU. In other words, networks using those activation functions are capable of universal approximation. We further show that our necessary condition and sufficient condition coincide under a mild condition on activation functions: e.g., for an activation function $\sigma$, there exists a fixed-point number $x$ such that $\sigma(x)=0$. Namely, we find a necessary and sufficient condition for a large class of activation functions. We lastly show that even quantized networks using binary weights in $\{-1,1\}$ can also universally approximate for practical activation functions.

Expressive Power of ReLU and Step Networks under Floating-Point Operations

The study of the expressive power of neural networks has investigated the fundamental limits of neural networks. Most existing results assume real-valued inputs and parameters as well as exact operations during the evaluation of neural networks. However, neural networks are typically executed on computers that can only represent a tiny subset of the reals and apply inexact operations. In this work, we analyze the expressive power of neural networks under a more realistic setup: when we use floating-point numbers and operations. Our first set of results assumes floating-point operations where the significand of a float is represented by finite bits but its exponent can take any integer value. Under this setup, we show that neural networks using a binary threshold unit or ReLU can memorize any finite input/output pairs and can approximate any continuous function within a small error. We also show similar results on memorization and universal approximation when floating-point operations use finite bits for both significand and exponent; these results are applicable to many popular floating-point formats such as those defined in the IEEE 754 standard (e.g., 32-bit single-precision format) and bfloat16.

Minimum Width for Deep, Narrow MLP: A Diffeomorphism and the Whitney Embedding Theorem Approach

Recently, there has been significant attention on determining the minimum width for the universal approximation property of deep, narrow MLPs. Among these challenges, approximating a continuous function under the uniform norm is important and challenging, with the gap between its lower and upper bound being hard to narrow. In this regard, we propose a novel upper bound for the minimum width, given by $\operatorname{max}(2d_x+1, d_y) + \alpha(\sigma)$, to achieve uniform approximation in deep narrow MLPs, where $0\leq \alpha(\sigma)\leq 2$ represents the constant depending on the activation function. We demonstrate this bound through two key proofs. First, we establish that deep, narrow MLPs with little additional width can approximate diffeomorphisms. Secondly, we utilize the Whitney embedding theorem to show that any continuous function can be approximated by embeddings, further decomposed into linear transformations and diffeomorphisms.

Minimal Width for Universal Property of Deep RNN

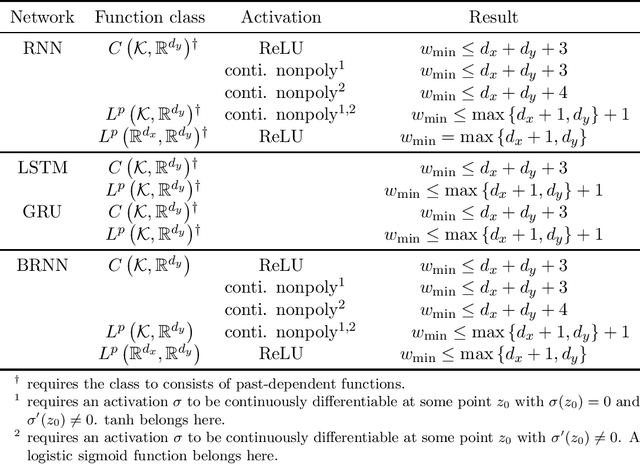
A recurrent neural network (RNN) is a widely used deep-learning network for dealing with sequential data. Imitating a dynamical system, an infinite-width RNN can approximate any open dynamical system in a compact domain. In general, deep networks with bounded widths are more effective than wide networks in practice; however, the universal approximation theorem for deep narrow structures has yet to be extensively studied. In this study, we prove the universality of deep narrow RNNs and show that the upper bound of the minimum width for universality can be independent of the length of the data. Specifically, we show that a deep RNN with ReLU activation can approximate any continuous function or $L^p$ function with the widths $d_x+d_y+2$ and $\max\{d_x+1,d_y\}$, respectively, where the target function maps a finite sequence of vectors in $\mathbb{R}^{d_x}$ to a finite sequence of vectors in $\mathbb{R}^{d_y}$. We also compute the additional width required if the activation function is $\tanh$ or more. In addition, we prove the universality of other recurrent networks, such as bidirectional RNNs. Bridging a multi-layer perceptron and an RNN, our theory and proof technique can be an initial step toward further research on deep RNNs.

Universal Property of Convolutional Neural Networks

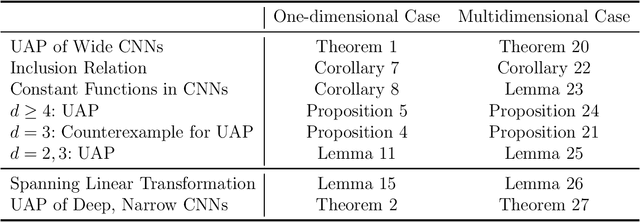
Universal approximation, whether a set of functions can approximate an arbitrary function in a specific function space, has been actively studied in recent years owing to the significant development of neural networks. However, despite its extensive use, research on the universal properties of the convolutional neural network has been limited due to its complex nature. In this regard, we demonstrate the universal approximation theorem for convolutional neural networks. A convolution with padding outputs the data of the same shape as the input data; therefore, it is necessary to prove whether a convolutional neural network composed of convolutions can approximate such a function. We have shown that convolutional neural networks can approximate continuous functions whose input and output values have the same shape. In addition, the minimum depth of the neural network required for approximation was presented, and we proved that it is the optimal value. We also verified that convolutional neural networks with sufficiently deep layers have universality when the number of channels is limited.

Finding the global semantic representation in GAN through Frechet Mean

The ideally disentangled latent space in GAN involves the global representation of latent space using semantic attribute coordinates. In other words, in this disentangled space, there exists the global semantic basis as a vector space where each basis component describes one attribute of generated images. In this paper, we propose an unsupervised method for finding this global semantic basis in the intermediate latent space in GANs. This semantic basis represents sample-independent meaningful perturbations that change the same semantic attribute of an image on the entire latent space. The proposed global basis, called Fr\'echet basis, is derived by introducing Fr\'echet mean to the local semantic perturbations in a latent space. Fr\'echet basis is discovered in two stages. First, the global semantic subspace is discovered by the Fr\'echet mean in the Grassmannian manifold of the local semantic subspaces. Second, Fr\'echet basis is found by optimizing a basis of the semantic subspace via the Fr\'echet mean in the Special Orthogonal Group. Experimental results demonstrate that Fr\'echet basis provides better semantic factorization and robustness compared to the previous methods. Moreover, we suggest the basis refinement scheme for the previous methods. The quantitative experiments show that the refined basis achieves better semantic factorization while generating the same semantic subspace as the previous method.

Analyzing the Latent Space of GAN through Local Dimension Estimation

The impressive success of style-based GANs (StyleGANs) in high-fidelity image synthesis has motivated research to understand the semantic properties of their latent spaces. Recently, a close relationship was observed between the semantically disentangled local perturbations and the local PCA components in the learned latent space $\mathcal{W}$. However, understanding the number of disentangled perturbations remains challenging. Building upon this observation, we propose a local dimension estimation algorithm for an arbitrary intermediate layer in a pre-trained GAN model. The estimated intrinsic dimension corresponds to the number of disentangled local perturbations. In this perspective, we analyze the intermediate layers of the mapping network in StyleGANs. Our analysis clarifies the success of $\mathcal{W}$-space in StyleGAN and suggests an alternative. Moreover, the intrinsic dimension estimation opens the possibility of unsupervised evaluation of global-basis-compatibility and disentanglement for a latent space. Our proposed metric, called Distortion, measures an inconsistency of intrinsic tangent space on the learned latent space. The metric is purely geometric and does not require any additional attribute information. Nevertheless, the metric shows a high correlation with the global-basis-compatibility and supervised disentanglement score. Our findings pave the way towards an unsupervised selection of globally disentangled latent space among the intermediate latent spaces in a GAN.

Do Not Escape From the Manifold: Discovering the Local Coordinates on the Latent Space of GANs

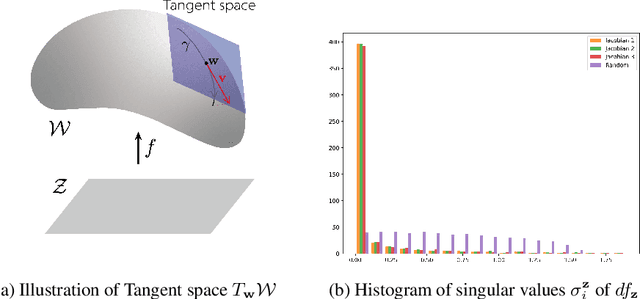
In this paper, we propose a method to find local-geometry-aware traversal directions on the intermediate latent space of Generative Adversarial Networks (GANs). These directions are defined as an ordered basis of tangent space at a latent code. Motivated by the intrinsic sparsity of the latent space, the basis is discovered by solving the low-rank approximation problem of the differential of the partial network. Moreover, the local traversal basis leads to a natural iterative traversal on the latent space. Iterative Curve-Traversal shows stable traversal on images, since the trajectory of latent code stays close to the latent space even under the strong perturbations compared to the linear traversal. This stability provides far more diverse variations of the given image. Although the proposed method can be applied to various GAN models, we focus on the W-space of the StyleGAN2, which is renowned for showing the better disentanglement of the latent factors of variation. Our quantitative and qualitative analysis provides evidence showing that the W-space is still globally warped while showing a certain degree of global consistency of interpretable variation. In particular, we introduce some metrics on the Grassmannian manifolds to quantify the global warpage of the W-space and the subspace traversal to test the stability of traversal directions.

Discond-VAE: Disentangling Continuous Factors from the Discrete

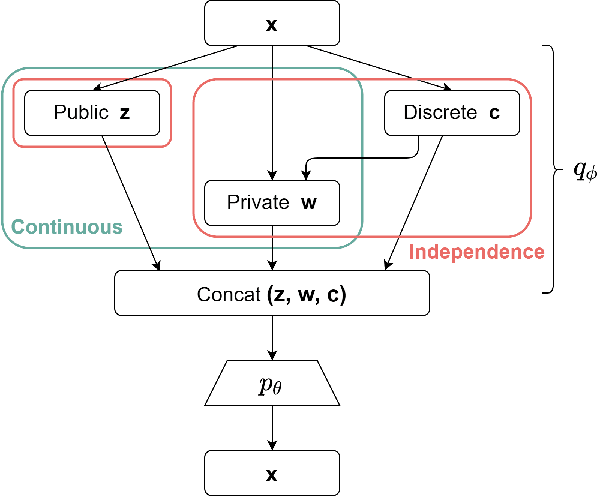
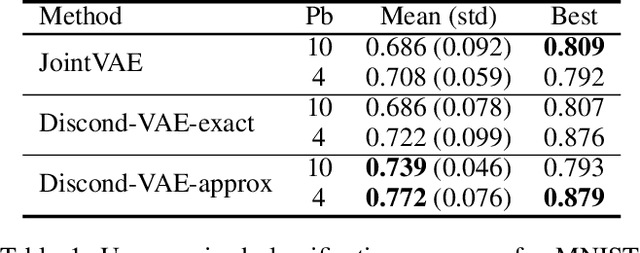
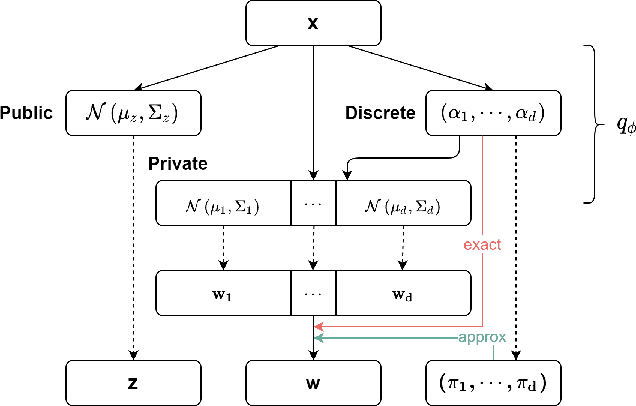
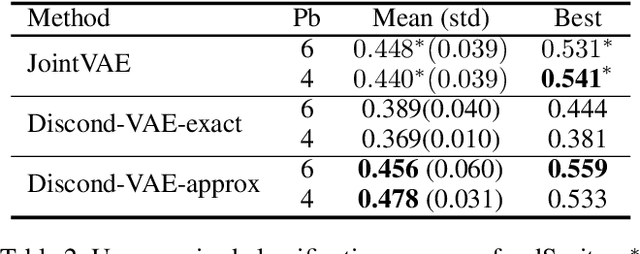
We propose a variant of VAE capable of disentangling both variations within each class and variations shared across all classes. To represent these generative factors of data, we introduce two sets of continuous latent variables, private variable and public variable. Our proposed framework models the private variable as a Mixture of Gaussian and the public variable as a Gaussian, respectively. Each mode of the private variable is responsible for a class of the discrete variable. Most of the previous attempts to integrate the discrete generative factors to disentanglement assume statistical independence between the continuous and discrete variables. However, this assumption does not hold in general. Our proposed model, which we call Discond-VAE, DISentangles the class-dependent CONtinuous factors from the Discrete factors by introducing the private variables. The experiments show that Discond-VAE can discover the private and public factors from data qualitatively and quantitatively.