Floating-Point Networks with Automatic Differentiation Can Represent Almost All Floating-Point Functions and Their Gradients

Theoretical studies show that for any differentiable function on a compact domain, there exists a neural network that approximates both the function values and gradients. However, such a result cannot be used in practice since it assumes real parameters and exact internal operations. In contrast, real implementations only use a finite subset of reals and machine operations with round-off errors. In this work, we investigate whether a similar result holds for neural networks under floating-point arithmetic, when the gradient with respect to the input is computed by the automatic differentiation algorithm $D^\mathtt{AD}$. We first show that given a floating-point function $φ$ (e.g., a loss function), arbitrary function values and gradients can be represented by a floating-point network $f$ and $D^\mathtt{AD}(φ\circ f)$, respectively. We further extend this result: given $φ_1,\dots,φ_n$, $D^\mathtt{AD}(φ_i\circ f)$ can simultaneously represent arbitrary gradients while $f$ represents the target values, under mild conditions. Our results hold for practical activation functions, e.g., $\mathrm{ReLU}$, $\mathrm{ELU}$, $\mathrm{GeLU}$, $\mathrm{Swish}$, $\mathrm{Sigmoid}$, and $\mathrm{tanh}$.

Intrinsic Task Symmetry Drives Generalization in Algorithmic Tasks

Grokking, the sudden transition from memorization to generalization, is characterized by the emergence of low-dimensional representations, yet the mechanism underlying this organization remains elusive. We propose that intrinsic task symmetries primarily drive grokking and shape the geometry of the model's representation space. We identify a consistent three-stage training dynamic underlying grokking: (i) memorization, (ii) symmetry acquisition, and (iii) geometric organization. We show that generalization emerges during the symmetry acquisition phase, after which representations reorganize into a structured, task-aligned geometry. We validate this symmetry-driven account across diverse algorithmic domains, including algebraic, structural, and relational reasoning tasks. Building on these findings, we introduce a symmetry-based diagnostic that anticipates the onset of generalization and propose strategies to accelerate it. Together, our results establish intrinsic symmetry as the key factor enabling neural networks to move beyond memorization and achieve robust algorithmic reasoning.

On the Expressive Power of Floating-Point Transformers

The study on the expressive power of transformers shows that transformers are permutation equivariant, and they can approximate all permutation-equivariant continuous functions on a compact domain. However, these results are derived under real parameters and exact operations, while real implementations on computers can only use a finite set of numbers and inexact machine operations with round-off errors. In this work, we investigate the representability of floating-point transformers that use floating-point parameters and floating-point operations. Unlike existing results under exact operations, we first show that floating-point transformers can represent a class of non-permutation-equivariant functions even without positional encoding. Furthermore, we prove that floating-point transformers can represent all permutation-equivariant functions when the sequence length is bounded, but they cannot when the sequence length is large. We also found the minimal equivariance structure in floating-point transformers, and show that all non-trivial additive positional encoding can harm the representability of floating-point transformers.

On Expressive Power of Quantized Neural Networks under Fixed-Point Arithmetic

Research into the expressive power of neural networks typically considers real parameters and operations without rounding error. In this work, we study universal approximation property of quantized networks under discrete fixed-point parameters and fixed-point operations that may incur errors due to rounding. We first provide a necessary condition and a sufficient condition on fixed-point arithmetic and activation functions for universal approximation of quantized networks. Then, we show that various popular activation functions satisfy our sufficient condition, e.g., Sigmoid, ReLU, ELU, SoftPlus, SiLU, Mish, and GELU. In other words, networks using those activation functions are capable of universal approximation. We further show that our necessary condition and sufficient condition coincide under a mild condition on activation functions: e.g., for an activation function $\sigma$, there exists a fixed-point number $x$ such that $\sigma(x)=0$. Namely, we find a necessary and sufficient condition for a large class of activation functions. We lastly show that even quantized networks using binary weights in $\{-1,1\}$ can also universally approximate for practical activation functions.

Absence of Closed-Form Descriptions for Gradient Flow in Two-Layer Narrow Networks

In the field of machine learning, comprehending the intricate training dynamics of neural networks poses a significant challenge. This paper explores the training dynamics of neural networks, particularly whether these dynamics can be expressed in a general closed-form solution. We demonstrate that the dynamics of the gradient flow in two-layer narrow networks is not an integrable system. Integrable systems are characterized by trajectories confined to submanifolds defined by level sets of first integrals (invariants), facilitating predictable and reducible dynamics. In contrast, non-integrable systems exhibit complex behaviors that are difficult to predict. To establish the non-integrability, we employ differential Galois theory, which focuses on the solvability of linear differential equations. We demonstrate that under mild conditions, the identity component of the differential Galois group of the variational equations of the gradient flow is non-solvable. This result confirms the system's non-integrability and implies that the training dynamics cannot be represented by Liouvillian functions, precluding a closed-form solution for describing these dynamics. Our findings highlight the necessity of employing numerical methods to tackle optimization problems within neural networks. The results contribute to a deeper understanding of neural network training dynamics and their implications for machine learning optimization strategies.

Acceleration of Grokking in Learning Arithmetic Operations via Kolmogorov-Arnold Representation

We propose novel methodologies aimed at accelerating the grokking phenomenon, which refers to the rapid increment of test accuracy after a long period of overfitting as reported in~\cite{power2022grokking}. Focusing on the grokking phenomenon that arises in learning arithmetic binary operations via the transformer model, we begin with a discussion on data augmentation in the case of commutative binary operations. To further accelerate, we elucidate arithmetic operations through the lens of the Kolmogorov-Arnold (KA) representation theorem, revealing its correspondence to the transformer architecture: embedding, decoder block, and classifier. Observing the shared structure between KA representations associated with binary operations, we suggest various transfer learning mechanisms that expedite grokking. This interpretation is substantiated through a series of rigorous experiments. In addition, our approach is successful in learning two nonstandard arithmetic tasks: composition of operations and a system of equations. Furthermore, we reveal that the model is capable of learning arithmetic operations using a limited number of tokens under embedding transfer, which is supported by a set of experiments as well.

Expressive Power of ReLU and Step Networks under Floating-Point Operations

The study of the expressive power of neural networks has investigated the fundamental limits of neural networks. Most existing results assume real-valued inputs and parameters as well as exact operations during the evaluation of neural networks. However, neural networks are typically executed on computers that can only represent a tiny subset of the reals and apply inexact operations. In this work, we analyze the expressive power of neural networks under a more realistic setup: when we use floating-point numbers and operations. Our first set of results assumes floating-point operations where the significand of a float is represented by finite bits but its exponent can take any integer value. Under this setup, we show that neural networks using a binary threshold unit or ReLU can memorize any finite input/output pairs and can approximate any continuous function within a small error. We also show similar results on memorization and universal approximation when floating-point operations use finite bits for both significand and exponent; these results are applicable to many popular floating-point formats such as those defined in the IEEE 754 standard (e.g., 32-bit single-precision format) and bfloat16.

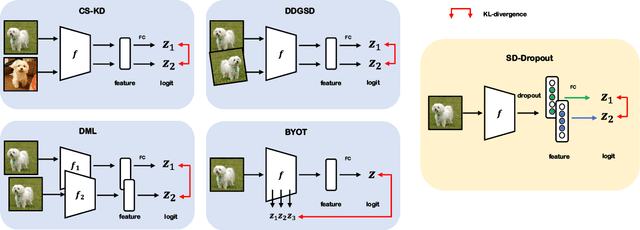
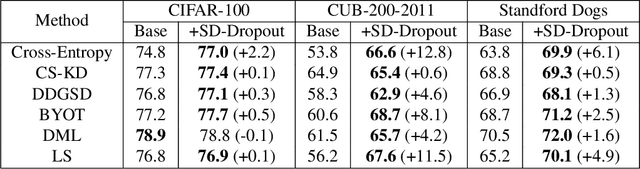
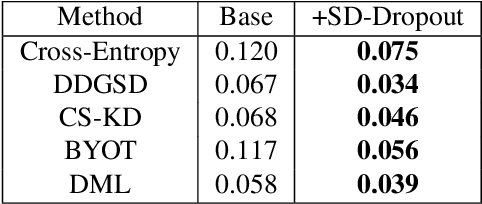
Self-Knowledge Distillation via Dropout

To boost the performance, deep neural networks require deeper or wider network structures that involve massive computational and memory costs. To alleviate this issue, the self-knowledge distillation method regularizes the model by distilling the internal knowledge of the model itself. Conventional self-knowledge distillation methods require additional trainable parameters or are dependent on the data. In this paper, we propose a simple and effective self-knowledge distillation method using a dropout (SD-Dropout). SD-Dropout distills the posterior distributions of multiple models through a dropout sampling. Our method does not require any additional trainable modules, does not rely on data, and requires only simple operations. Furthermore, this simple method can be easily combined with various self-knowledge distillation approaches. We provide a theoretical and experimental analysis of the effect of forward and reverse KL-divergences in our work. Extensive experiments on various vision tasks, i.e., image classification, object detection, and distribution shift, demonstrate that the proposed method can effectively improve the generalization of a single network. Further experiments show that the proposed method also improves calibration performance, adversarial robustness, and out-of-distribution detection ability.

MARA-Net: Single Image Deraining Network with Multi-level connections and Adaptive Regional Attentions

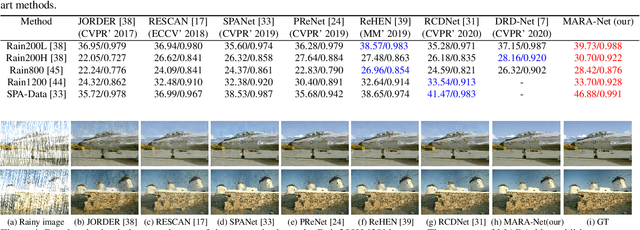
Removing rain streaks from single images is an important problem in various computer vision tasks because rain streaks can degrade outdoor images and reduce their visibility. While recent convolutional neural network-based deraining models have succeeded in capturing rain streaks effectively, difficulties in recovering the details in rain-free images still remain. In this paper, we present a multi-level connection and adaptive regional attention network (MARA-Net) to properly restore the original background textures in rainy images. The first main idea is a multi-level connection design that repeatedly connects multi-level features of the encoder network to the decoder network. Multi-level connections encourage the decoding process to use the feature information of all levels. Channel attention is considered in multi-level connections to learn which level of features is important in the decoding process of the current level. The second main idea is a wide regional non-local block (WRNL). As rain streaks primarily exhibit a vertical distribution, we divide the grid of the image into horizontally-wide patches and apply a non-local operation to each region to explore the rich rain-free background information. Experimental results on both synthetic and real-world rainy datasets demonstrate that the proposed model significantly outperforms existing state-of-the-art models. Furthermore, the results of the joint deraining and segmentation experiment prove that our model contributes effectively to other vision tasks.

Membership Inference Attacks Against Object Detection Models

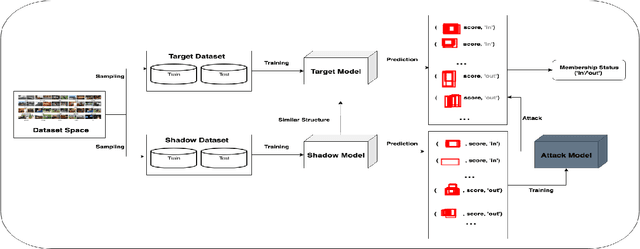
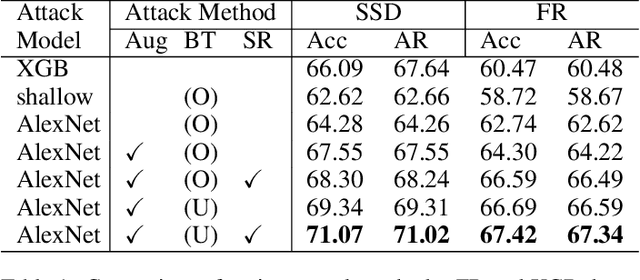
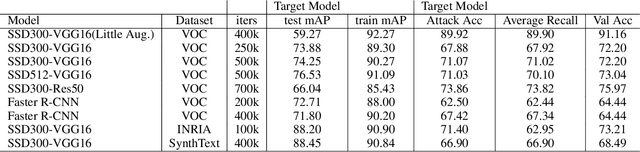
Machine learning models can leak information regarding the dataset they have trained. In this paper, we present the first membership inference attack against black-boxed object detection models that determines whether the given data records are used in the training. To attack the object detection model, we devise a novel method named as called a canvas method, in which predicted bounding boxes are drawn on an empty image for the attack model input. Based on the experiments, we successfully reveal the membership status of privately sensitive data trained using one-stage and two-stage detection models. We then propose defense strategies and also conduct a transfer attack between the models and datasets. Our results show that object detection models are also vulnerable to inference attacks like other models.