Deep Reinforcement Learning for the Design of Metamaterial Mechanisms with Functional Compliance Control

Metamaterial mechanisms are micro-architectured compliant structures that operate through the elastic deformation of specially designed flexible members. This study develops an efficient design methodology for compliant mechanisms using deep reinforcement learning (RL). For this purpose, design domains are digitized into finite cells with various hinge connections, and finite element analyses (FEAs) are conducted to evaluate the deformation behaviors of the compliance mechanism with different cell combinations. The FEA data are learned through the RL method to obtain optimal compliant mechanisms for desired functional requirements. The RL algorithm is applied to the design of a compliant door-latch mechanism, exploring the effect of human guidance and tiling direction. The optimal result is achieved with minimal human guidance and inward tiling, resulting in a threefold increase in the predefined reward compared to human-designed mechanisms. The proposed approach is extended to the design of a soft gripper mechanism, where the effect of hinge connections is additionally considered. The optimal design under hinge penalization reveals remarkably enhanced compliance, and its performance is validated by experimental tests using an additively manufactured gripper. These findings demonstrate that RL-optimized designs outperform those developed with human insight, providing an efficient design methodology for cell-based compliant mechanisms in practical applications.

Hamilton-Jacobi Based Policy-Iteration via Deep Operator Learning

The framework of deep operator network (DeepONet) has been widely exploited thanks to its capability of solving high dimensional partial differential equations. In this paper, we incorporate DeepONet with a recently developed policy iteration scheme to numerically solve optimal control problems and the corresponding Hamilton--Jacobi--Bellman (HJB) equations. A notable feature of our approach is that once the neural network is trained, the solution to the optimal control problem and HJB equations with different terminal functions can be inferred quickly thanks to the unique feature of operator learning. Furthermore, a quantitative analysis of the accuracy of the algorithm is carried out via comparison principles of viscosity solutions. The effectiveness of the method is verified with various examples, including 10-dimensional linear quadratic regulator problems (LQRs).

Approximate Thompson Sampling for Learning Linear Quadratic Regulators with $O(\sqrt{T})$ Regret

We propose an approximate Thompson sampling algorithm that learns linear quadratic regulators (LQR) with an improved Bayesian regret bound of $O(\sqrt{T})$. Our method leverages Langevin dynamics with a meticulously designed preconditioner as well as a simple excitation mechanism. We show that the excitation signal induces the minimum eigenvalue of the preconditioner to grow over time, thereby accelerating the approximate posterior sampling process. Moreover, we identify nontrivial concentration properties of the approximate posteriors generated by our algorithm. These properties enable us to bound the moments of the system state and attain an $O(\sqrt{T})$ regret bound without the unrealistic restrictive assumptions on parameter sets that are often used in the literature.

Acceleration of Grokking in Learning Arithmetic Operations via Kolmogorov-Arnold Representation

We propose novel methodologies aimed at accelerating the grokking phenomenon, which refers to the rapid increment of test accuracy after a long period of overfitting as reported in~\cite{power2022grokking}. Focusing on the grokking phenomenon that arises in learning arithmetic binary operations via the transformer model, we begin with a discussion on data augmentation in the case of commutative binary operations. To further accelerate, we elucidate arithmetic operations through the lens of the Kolmogorov-Arnold (KA) representation theorem, revealing its correspondence to the transformer architecture: embedding, decoder block, and classifier. Observing the shared structure between KA representations associated with binary operations, we suggest various transfer learning mechanisms that expedite grokking. This interpretation is substantiated through a series of rigorous experiments. In addition, our approach is successful in learning two nonstandard arithmetic tasks: composition of operations and a system of equations. Furthermore, we reveal that the model is capable of learning arithmetic operations using a limited number of tokens under embedding transfer, which is supported by a set of experiments as well.

On the stability of Lipschitz continuous control problems and its application to reinforcement learning

We address the crucial yet underexplored stability properties of the Hamilton--Jacobi--Bellman (HJB) equation in model-free reinforcement learning contexts, specifically for Lipschitz continuous optimal control problems. We bridge the gap between Lipschitz continuous optimal control problems and classical optimal control problems in the viscosity solutions framework, offering new insights into the stability of the value function of Lipschitz continuous optimal control problems. By introducing structural assumptions on the dynamics and reward functions, we further study the rate of convergence of value functions. Moreover, we introduce a generalized framework for Lipschitz continuous control problems that incorporates the original problem and leverage it to propose a new HJB-based reinforcement learning algorithm. The stability properties and performance of the proposed method are tested with well-known benchmark examples in comparison with existing approaches.

Improved Regret Analysis for Variance-Adaptive Linear Bandits and Horizon-Free Linear Mixture MDPs

In online learning problems, exploiting low variance plays an important role in obtaining tight performance guarantees yet is challenging because variances are often not known a priori. Recently, a considerable progress has been made by Zhang et al. (2021) where they obtain a variance-adaptive regret bound for linear bandits without knowledge of the variances and a horizon-free regret bound for linear mixture Markov decision processes (MDPs). In this paper, we present novel analyses that improve their regret bounds significantly. For linear bandits, we achieve $\tilde O(d^{1.5}\sqrt{\sum_{k}^K \sigma_k^2} + d^2)$ where $d$ is the dimension of the features, $K$ is the time horizon, and $\sigma_k^2$ is the noise variance at time step $k$, and $\tilde O$ ignores polylogarithmic dependence, which is a factor of $d^3$ improvement. For linear mixture MDPs, we achieve a horizon-free regret bound of $\tilde O(d^{1.5}\sqrt{K} + d^3)$ where $d$ is the number of base models and $K$ is the number of episodes. This is a factor of $d^3$ improvement in the leading term and $d^6$ in the lower order term. Our analysis critically relies on a novel elliptical potential `count' lemma. This lemma allows a peeling-based regret analysis, which can be of independent interest.

Training Wasserstein GANs without gradient penalties

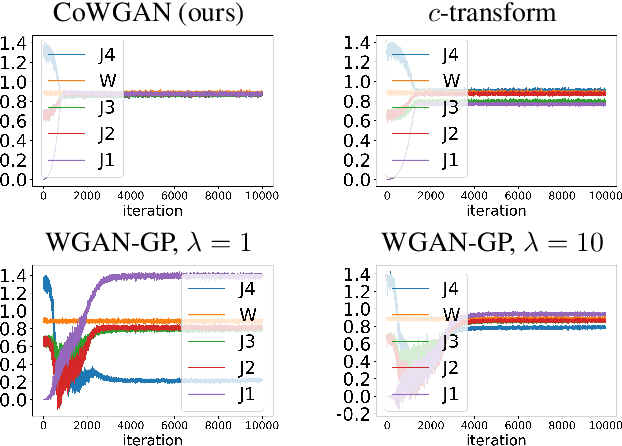
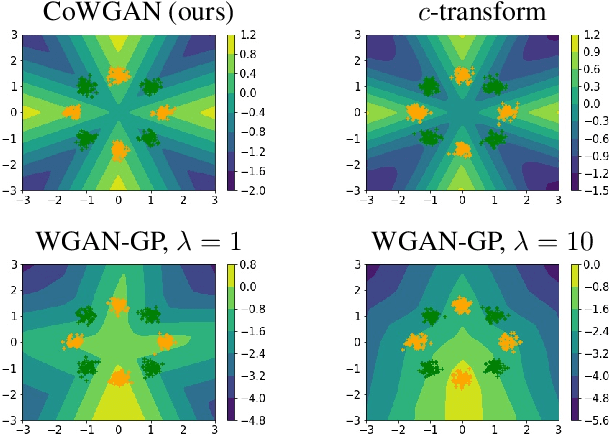
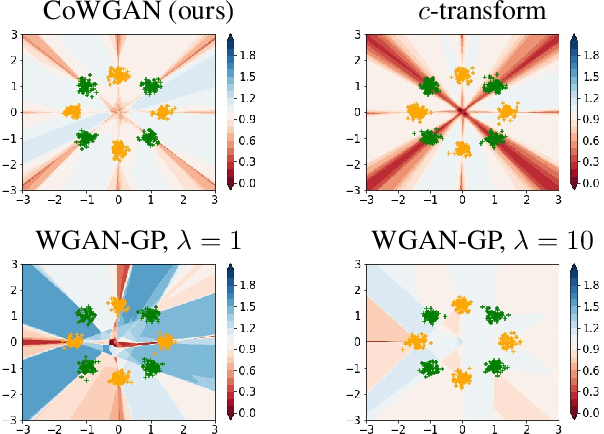
We propose a stable method to train Wasserstein generative adversarial networks. In order to enhance stability, we consider two objective functions using the $c$-transform based on Kantorovich duality which arises in the theory of optimal transport. We experimentally show that this algorithm can effectively enforce the Lipschitz constraint on the discriminator while other standard methods fail to do so. As a consequence, our method yields an accurate estimation for the optimal discriminator and also for the Wasserstein distance between the true distribution and the generated one. Our method requires no gradient penalties nor corresponding hyperparameter tuning and is computationally more efficient than other methods. At the same time, it yields competitive generators of synthetic images based on the MNIST, F-MNIST, and CIFAR-10 datasets.

Infusing model predictive control into meta-reinforcement learning for mobile robots in dynamic environments

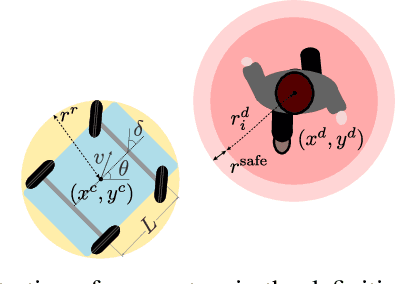
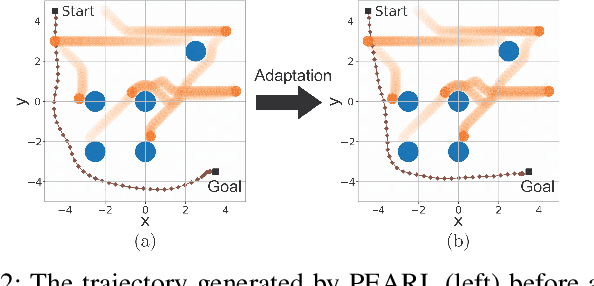
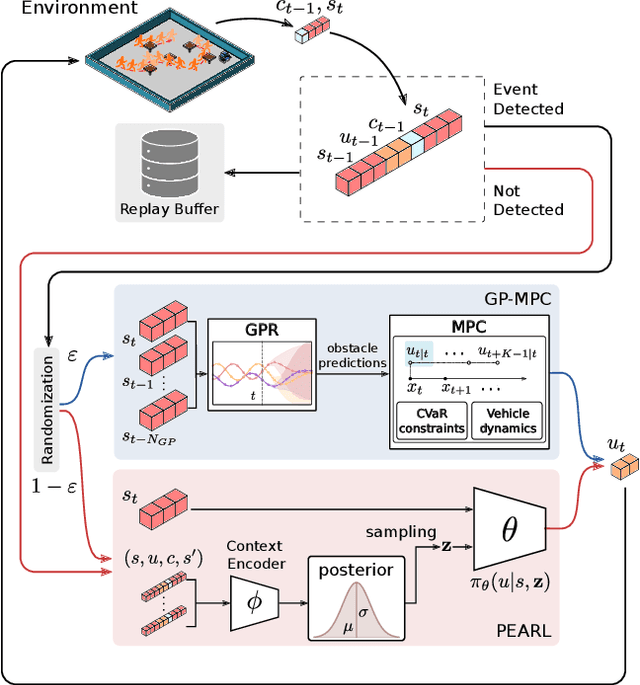
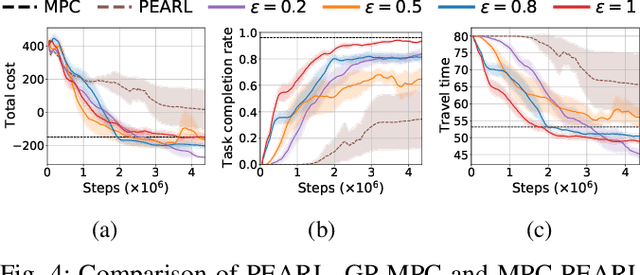
The successful operation of mobile robots requires them to rapidly adapt to environmental changes. Toward developing an adaptive decision-making tool for mobile robots, we propose combining meta-reinforcement learning (meta-RL) with model predictive control (MPC). The key idea of our method is to switch between a meta-learned policy and an MPC controller in an event-triggered fashion. Our method uses an off-policy meta-RL algorithm as a baseline to train a policy using transition samples generated by MPC. The MPC module of our algorithm is carefully designed to infer the movements of obstacles via Gaussian process regression (GPR) and to avoid collisions via conditional value-at-risk (CVaR) constraints. Due to its design, our method benefits from the two complementary tools. First, high-performance action samples generated by the MPC controller enhance the learning performance and stability of the meta-RL algorithm. Second, through the use of the meta-learned policy, the MPC controller is infrequently activated, thereby significantly reducing computation time. The results of our simulations on a restaurant service robot show that our algorithm outperforms both of the baseline methods.