KoopCast: Trajectory Forecasting via Koopman Operators

We present KoopCast, a lightweight yet efficient model for trajectory forecasting in general dynamic environments. Our approach leverages Koopman operator theory, which enables a linear representation of nonlinear dynamics by lifting trajectories into a higher-dimensional space. The framework follows a two-stage design: first, a probabilistic neural goal estimator predicts plausible long-term targets, specifying where to go; second, a Koopman operator-based refinement module incorporates intention and history into a nonlinear feature space, enabling linear prediction that dictates how to go. This dual structure not only ensures strong predictive accuracy but also inherits the favorable properties of linear operators while faithfully capturing nonlinear dynamics. As a result, our model offers three key advantages: (i) competitive accuracy, (ii) interpretability grounded in Koopman spectral theory, and (iii) low-latency deployment. We validate these benefits on ETH/UCY, the Waymo Open Motion Dataset, and nuScenes, which feature rich multi-agent interactions and map-constrained nonlinear motion. Across benchmarks, KoopCast consistently delivers high predictive accuracy together with mode-level interpretability and practical efficiency.

Egocentric Conformal Prediction for Safe and Efficient Navigation in Dynamic Cluttered Environments

Conformal prediction (CP) has emerged as a powerful tool in robotics and control, thanks to its ability to calibrate complex, data-driven models with formal guarantees. However, in robot navigation tasks, existing CP-based methods often decouple prediction from control, evaluating models without considering whether prediction errors actually compromise safety. Consequently, ego-vehicles may become overly conservative or even immobilized when all potential trajectories appear infeasible. To address this issue, we propose a novel CP-based navigation framework that responds exclusively to safety-critical prediction errors. Our approach introduces egocentric score functions that quantify how much closer obstacles are to a candidate vehicle position than anticipated. These score functions are then integrated into a model predictive control scheme, wherein each candidate state is individually evaluated for safety. Combined with an adaptive CP mechanism, our framework dynamically adjusts to changes in obstacle motion without resorting to unnecessary conservatism. Theoretical analyses indicate that our method outperforms existing CP-based approaches in terms of cost-efficiency while maintaining the desired safety levels, as further validated through experiments on real-world datasets featuring densely populated pedestrian environments.

On Task-Relevant Loss Functions in Meta-Reinforcement Learning and Online LQR

Designing a competent meta-reinforcement learning (meta-RL) algorithm in terms of data usage remains a central challenge to be tackled for its successful real-world applications. In this paper, we propose a sample-efficient meta-RL algorithm that learns a model of the system or environment at hand in a task-directed manner. As opposed to the standard model-based approaches to meta-RL, our method exploits the value information in order to rapidly capture the decision-critical part of the environment. The key component of our method is the loss function for learning the task inference module and the system model that systematically couples the model discrepancy and the value estimate, thereby facilitating the learning of the policy and the task inference module with a significantly smaller amount of data compared to the existing meta-RL algorithms. The idea is also extended to a non-meta-RL setting, namely an online linear quadratic regulator (LQR) problem, where our method can be simplified to reveal the essence of the strategy. The proposed method is evaluated in high-dimensional robotic control and online LQR problems, empirically verifying its effectiveness in extracting information indispensable for solving the tasks from observations in a sample efficient manner.

Infusing model predictive control into meta-reinforcement learning for mobile robots in dynamic environments

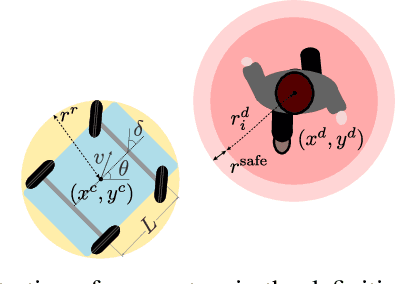
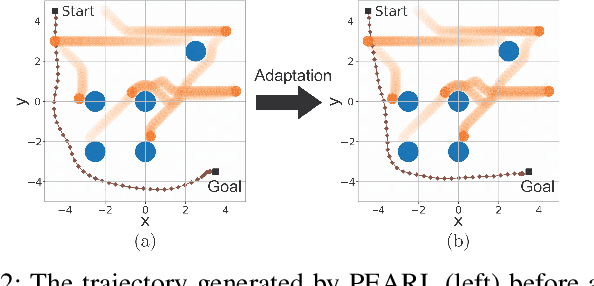
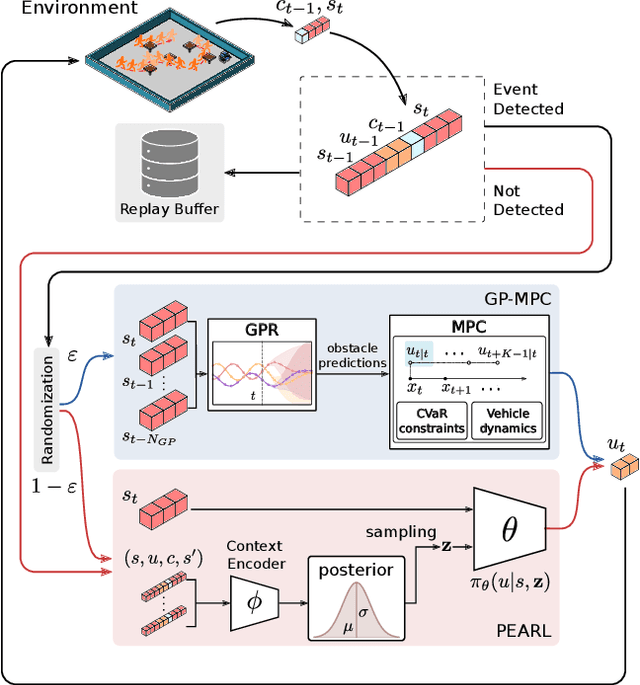
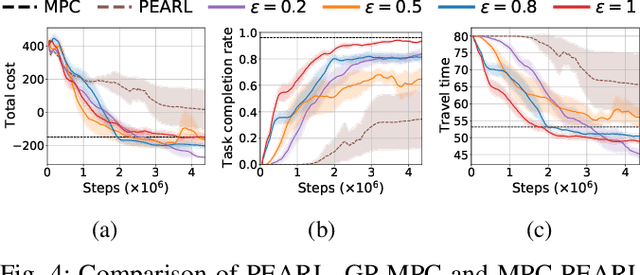
The successful operation of mobile robots requires them to rapidly adapt to environmental changes. Toward developing an adaptive decision-making tool for mobile robots, we propose combining meta-reinforcement learning (meta-RL) with model predictive control (MPC). The key idea of our method is to switch between a meta-learned policy and an MPC controller in an event-triggered fashion. Our method uses an off-policy meta-RL algorithm as a baseline to train a policy using transition samples generated by MPC. The MPC module of our algorithm is carefully designed to infer the movements of obstacles via Gaussian process regression (GPR) and to avoid collisions via conditional value-at-risk (CVaR) constraints. Due to its design, our method benefits from the two complementary tools. First, high-performance action samples generated by the MPC controller enhance the learning performance and stability of the meta-RL algorithm. Second, through the use of the meta-learned policy, the MPC controller is infrequently activated, thereby significantly reducing computation time. The results of our simulations on a restaurant service robot show that our algorithm outperforms both of the baseline methods.

Hamilton-Jacobi Deep Q-Learning for Deterministic Continuous-Time Systems with Lipschitz Continuous Controls

In this paper, we propose Q-learning algorithms for continuous-time deterministic optimal control problems with Lipschitz continuous controls. Our method is based on a new class of Hamilton-Jacobi-Bellman (HJB) equations derived from applying the dynamic programming principle to continuous-time Q-functions. A novel semi-discrete version of the HJB equation is proposed to design a Q-learning algorithm that uses data collected in discrete time without discretizing or approximating the system dynamics. We identify the condition under which the Q-function estimated by this algorithm converges to the optimal Q-function. For practical implementation, we propose the Hamilton-Jacobi DQN, which extends the idea of deep Q-networks (DQN) to our continuous control setting. This approach does not require actor networks or numerical solutions to optimization problems for greedy actions since the HJB equation provides a simple characterization of optimal controls via ordinary differential equations. We empirically demonstrate the performance of our method through benchmark tasks and high-dimensional linear-quadratic problems.