KoopCast: Trajectory Forecasting via Koopman Operators

We present KoopCast, a lightweight yet efficient model for trajectory forecasting in general dynamic environments. Our approach leverages Koopman operator theory, which enables a linear representation of nonlinear dynamics by lifting trajectories into a higher-dimensional space. The framework follows a two-stage design: first, a probabilistic neural goal estimator predicts plausible long-term targets, specifying where to go; second, a Koopman operator-based refinement module incorporates intention and history into a nonlinear feature space, enabling linear prediction that dictates how to go. This dual structure not only ensures strong predictive accuracy but also inherits the favorable properties of linear operators while faithfully capturing nonlinear dynamics. As a result, our model offers three key advantages: (i) competitive accuracy, (ii) interpretability grounded in Koopman spectral theory, and (iii) low-latency deployment. We validate these benefits on ETH/UCY, the Waymo Open Motion Dataset, and nuScenes, which feature rich multi-agent interactions and map-constrained nonlinear motion. Across benchmarks, KoopCast consistently delivers high predictive accuracy together with mode-level interpretability and practical efficiency.

Egocentric Conformal Prediction for Safe and Efficient Navigation in Dynamic Cluttered Environments

Conformal prediction (CP) has emerged as a powerful tool in robotics and control, thanks to its ability to calibrate complex, data-driven models with formal guarantees. However, in robot navigation tasks, existing CP-based methods often decouple prediction from control, evaluating models without considering whether prediction errors actually compromise safety. Consequently, ego-vehicles may become overly conservative or even immobilized when all potential trajectories appear infeasible. To address this issue, we propose a novel CP-based navigation framework that responds exclusively to safety-critical prediction errors. Our approach introduces egocentric score functions that quantify how much closer obstacles are to a candidate vehicle position than anticipated. These score functions are then integrated into a model predictive control scheme, wherein each candidate state is individually evaluated for safety. Combined with an adaptive CP mechanism, our framework dynamically adjusts to changes in obstacle motion without resorting to unnecessary conservatism. Theoretical analyses indicate that our method outperforms existing CP-based approaches in terms of cost-efficiency while maintaining the desired safety levels, as further validated through experiments on real-world datasets featuring densely populated pedestrian environments.

Generalized Continuous-Time Models for Nesterov's Accelerated Gradient Methods

Recent research has indicated a substantial rise in interest in understanding Nesterov's accelerated gradient methods via their continuous-time models. However, most existing studies focus on specific classes of Nesterov's methods, which hinders the attainment of an in-depth understanding and a unified perspective. To address this deficit, we present generalized continuous-time models that cover a broad range of Nesterov's methods, including those previously studied under existing continuous-time frameworks. Our key contributions are as follows. First, we identify the convergence rates of the generalized models, eliminating the need to determine the convergence rate for any specific continuous-time model derived from them. Second, we show that six existing continuous-time models are special cases of our generalized models, thereby positioning our framework as a unifying tool for analyzing and understanding these models. Third, we design a restart scheme for Nesterov's methods based on our generalized models and show that it ensures a monotonic decrease in objective function values. Owing to the broad applicability of our models, this scheme can be used to a broader class of Nesterov's methods compared to the original restart scheme. Fourth, we uncover a connection between our generalized models and gradient flow in continuous time, showing that the accelerated convergence rates of our generalized models can be attributed to a time reparametrization in gradient flow. Numerical experiment results are provided to support our theoretical analyses and results.

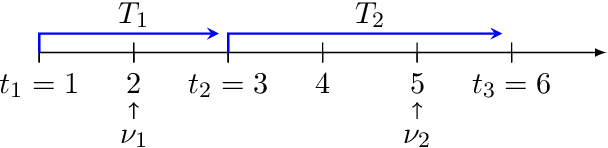
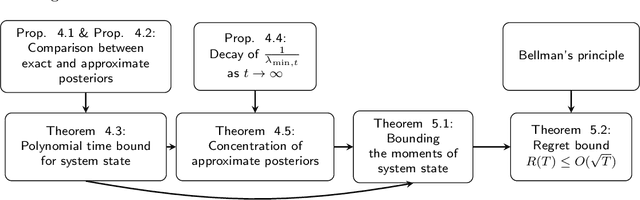
Approximate Thompson Sampling for Learning Linear Quadratic Regulators with $O(\sqrt{T})$ Regret

We propose an approximate Thompson sampling algorithm that learns linear quadratic regulators (LQR) with an improved Bayesian regret bound of $O(\sqrt{T})$. Our method leverages Langevin dynamics with a meticulously designed preconditioner as well as a simple excitation mechanism. We show that the excitation signal induces the minimum eigenvalue of the preconditioner to grow over time, thereby accelerating the approximate posterior sampling process. Moreover, we identify nontrivial concentration properties of the approximate posteriors generated by our algorithm. These properties enable us to bound the moments of the system state and attain an $O(\sqrt{T})$ regret bound without the unrealistic restrictive assumptions on parameter sets that are often used in the literature.

On Task-Relevant Loss Functions in Meta-Reinforcement Learning and Online LQR

Designing a competent meta-reinforcement learning (meta-RL) algorithm in terms of data usage remains a central challenge to be tackled for its successful real-world applications. In this paper, we propose a sample-efficient meta-RL algorithm that learns a model of the system or environment at hand in a task-directed manner. As opposed to the standard model-based approaches to meta-RL, our method exploits the value information in order to rapidly capture the decision-critical part of the environment. The key component of our method is the loss function for learning the task inference module and the system model that systematically couples the model discrepancy and the value estimate, thereby facilitating the learning of the policy and the task inference module with a significantly smaller amount of data compared to the existing meta-RL algorithms. The idea is also extended to a non-meta-RL setting, namely an online linear quadratic regulator (LQR) problem, where our method can be simplified to reveal the essence of the strategy. The proposed method is evaluated in high-dimensional robotic control and online LQR problems, empirically verifying its effectiveness in extracting information indispensable for solving the tasks from observations in a sample efficient manner.

Risk-Aware Wasserstein Distributionally Robust Control of Vessels in Natural Waterways

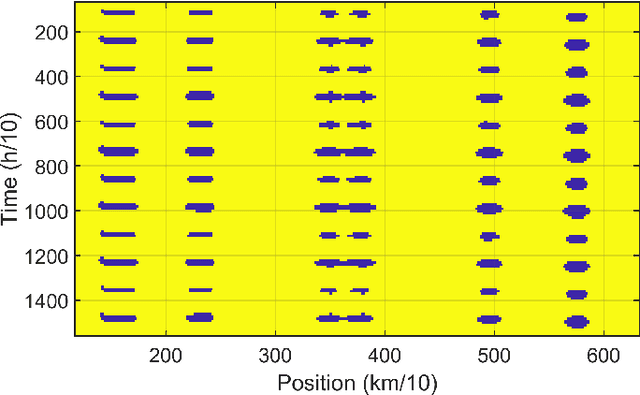
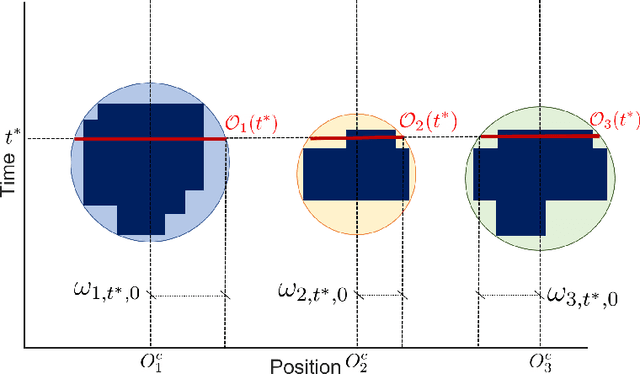
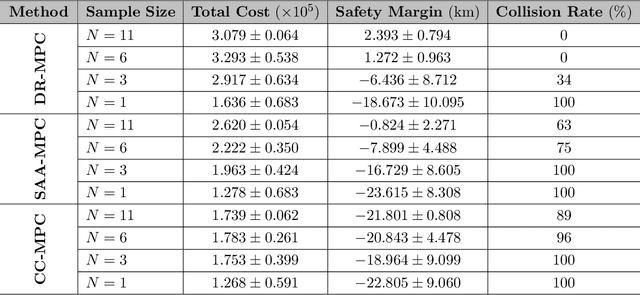
In the realm of maritime transportation, autonomous vessel navigation in natural inland waterways faces persistent challenges due to unpredictable natural factors. Existing scheduling algorithms fall short in handling these uncertainties, compromising both safety and efficiency. Moreover, these algorithms are primarily designed for non-autonomous vessels, leading to labor-intensive operations vulnerable to human error. To address these issues, this study proposes a risk-aware motion control approach for vessels that accounts for the dynamic and uncertain nature of tide islands in a distributionally robust manner. Specifically, a model predictive control method is employed to follow the reference trajectory in the time-space map while incorporating a risk constraint to prevent grounding accidents. To address uncertainties in tide islands, a novel modeling technique represents them as stochastic polytopes. Additionally, potential inaccuracies in waterway depth are addressed through a risk constraint that considers the worst-case uncertainty distribution within a Wasserstein ambiguity set around the empirical distribution. Using sensor data collected in the Guadalquivir River, we empirically demonstrate the performance of the proposed method through simulations on a vessel. As a result, the vessel successfully navigates the waterway while avoiding grounding accidents, even with a limited dataset of observations. This stands in contrast to existing non-robust controllers, highlighting the robustness and practical applicability of the proposed approach.

Improved Regret Analysis for Variance-Adaptive Linear Bandits and Horizon-Free Linear Mixture MDPs

In online learning problems, exploiting low variance plays an important role in obtaining tight performance guarantees yet is challenging because variances are often not known a priori. Recently, a considerable progress has been made by Zhang et al. (2021) where they obtain a variance-adaptive regret bound for linear bandits without knowledge of the variances and a horizon-free regret bound for linear mixture Markov decision processes (MDPs). In this paper, we present novel analyses that improve their regret bounds significantly. For linear bandits, we achieve $\tilde O(d^{1.5}\sqrt{\sum_{k}^K \sigma_k^2} + d^2)$ where $d$ is the dimension of the features, $K$ is the time horizon, and $\sigma_k^2$ is the noise variance at time step $k$, and $\tilde O$ ignores polylogarithmic dependence, which is a factor of $d^3$ improvement. For linear mixture MDPs, we achieve a horizon-free regret bound of $\tilde O(d^{1.5}\sqrt{K} + d^3)$ where $d$ is the number of base models and $K$ is the number of episodes. This is a factor of $d^3$ improvement in the leading term and $d^6$ in the lower order term. Our analysis critically relies on a novel elliptical potential `count' lemma. This lemma allows a peeling-based regret analysis, which can be of independent interest.

Training Wasserstein GANs without gradient penalties

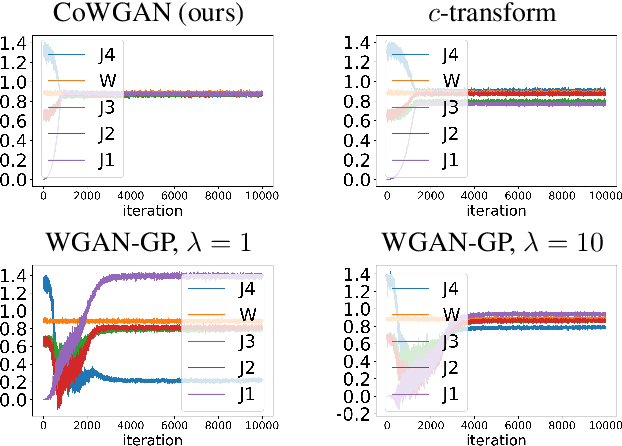
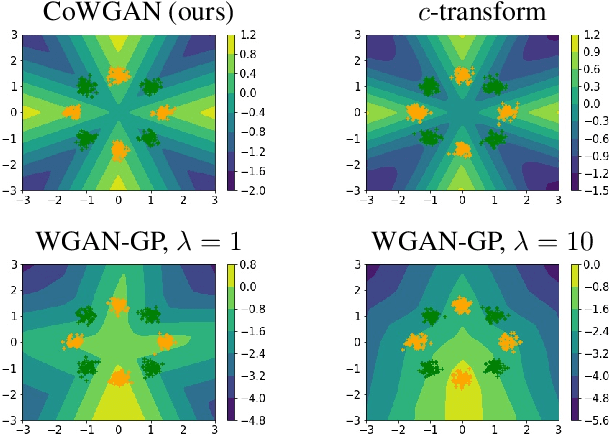
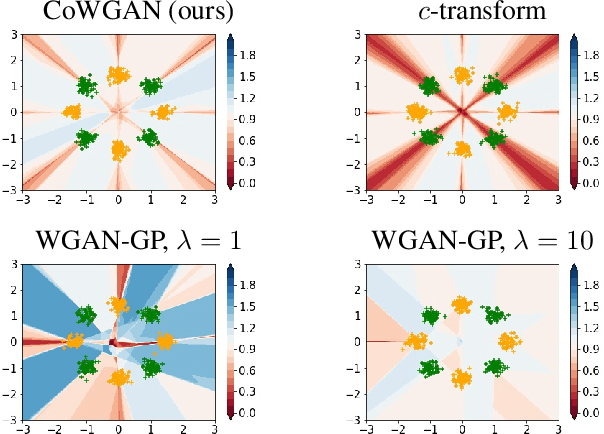
We propose a stable method to train Wasserstein generative adversarial networks. In order to enhance stability, we consider two objective functions using the $c$-transform based on Kantorovich duality which arises in the theory of optimal transport. We experimentally show that this algorithm can effectively enforce the Lipschitz constraint on the discriminator while other standard methods fail to do so. As a consequence, our method yields an accurate estimation for the optimal discriminator and also for the Wasserstein distance between the true distribution and the generated one. Our method requires no gradient penalties nor corresponding hyperparameter tuning and is computationally more efficient than other methods. At the same time, it yields competitive generators of synthetic images based on the MNIST, F-MNIST, and CIFAR-10 datasets.

Infusing model predictive control into meta-reinforcement learning for mobile robots in dynamic environments

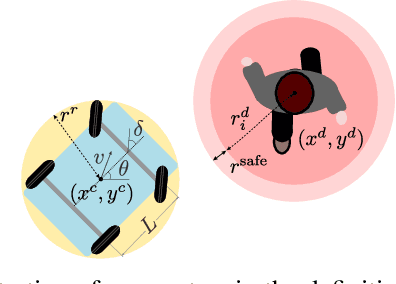
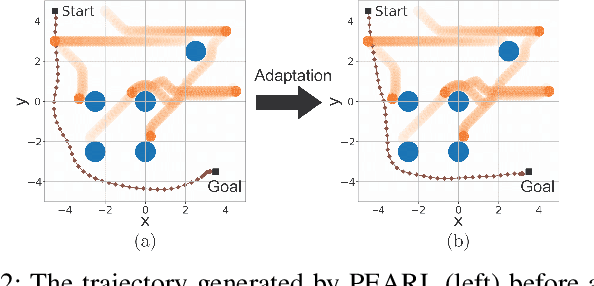
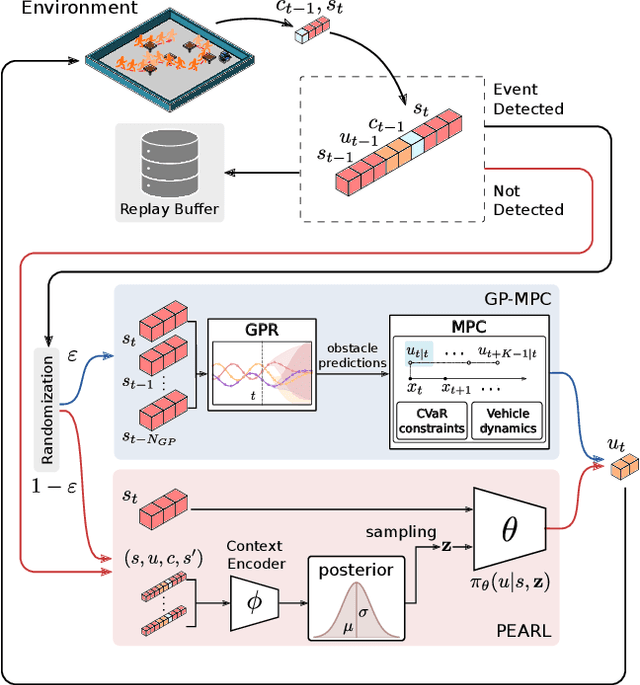
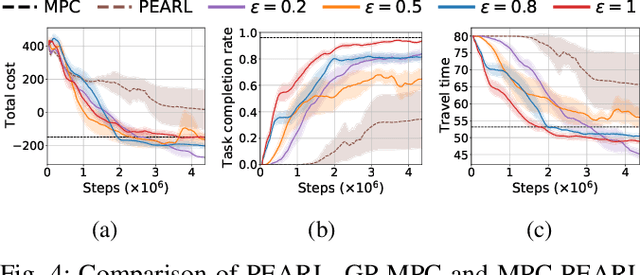
The successful operation of mobile robots requires them to rapidly adapt to environmental changes. Toward developing an adaptive decision-making tool for mobile robots, we propose combining meta-reinforcement learning (meta-RL) with model predictive control (MPC). The key idea of our method is to switch between a meta-learned policy and an MPC controller in an event-triggered fashion. Our method uses an off-policy meta-RL algorithm as a baseline to train a policy using transition samples generated by MPC. The MPC module of our algorithm is carefully designed to infer the movements of obstacles via Gaussian process regression (GPR) and to avoid collisions via conditional value-at-risk (CVaR) constraints. Due to its design, our method benefits from the two complementary tools. First, high-performance action samples generated by the MPC controller enhance the learning performance and stability of the meta-RL algorithm. Second, through the use of the meta-learned policy, the MPC controller is infrequently activated, thereby significantly reducing computation time. The results of our simulations on a restaurant service robot show that our algorithm outperforms both of the baseline methods.

Distributionally robust risk map for learning-based motion planning and control: A semidefinite programming approach

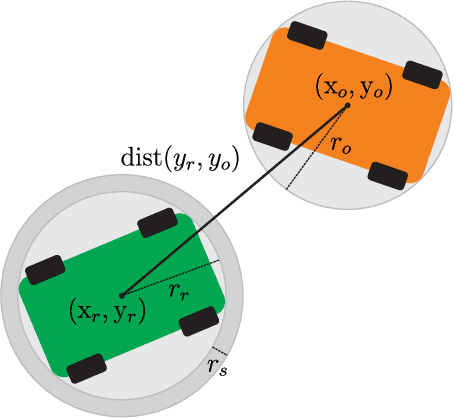
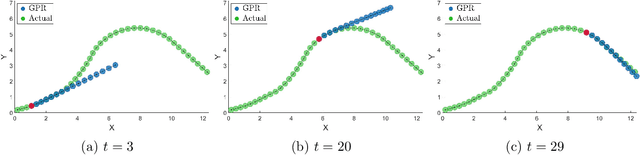
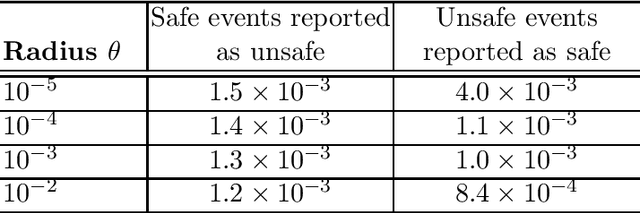
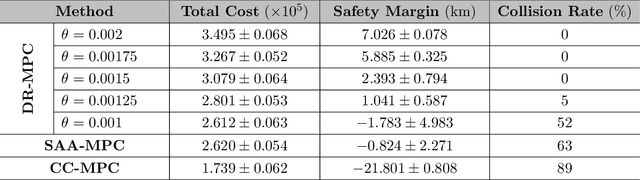
This paper proposes a novel safety specification tool, called the distributionally robust risk map (DR-risk map), for a mobile robot operating in a learning-enabled environment. Given the robot's position, the map aims to reliably assess the conditional value-at-risk (CVaR) of collision with obstacles whose movements are inferred by Gaussian process regression (GPR). Unfortunately, the inferred distribution is subject to errors, making it difficult to accurately evaluate the CVaR of collision. To overcome this challenge, this tool measures the risk under the worst-case distribution in a so-called ambiguity set that characterizes allowable distribution errors. To resolve the infinite-dimensionality issue inherent in the construction of the DR-risk map, we derive a tractable semidefinite programming formulation that provides an upper bound of the risk, exploiting techniques from modern distributionally robust optimization. As a concrete application for motion planning, a distributionally robust RRT* algorithm is considered using the risk map that addresses distribution errors caused by GPR. Furthermore, a motion control method is devised using the DR-risk map in a learning-based model predictive control (MPC) formulation. In particular, a neural network approximation of the risk map is proposed to reduce the computational cost in solving the MPC problem. The performance and utility of the proposed risk map are demonstrated through simulation studies that show its ability to ensure the safety of mobile robots despite learning errors.