Distributionally robust risk map for learning-based motion planning and control: A semidefinite programming approach
Paper and Code
May 03, 2021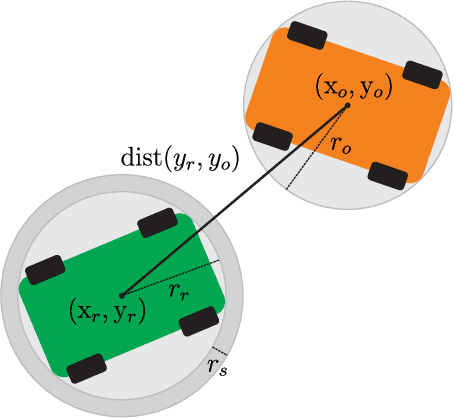

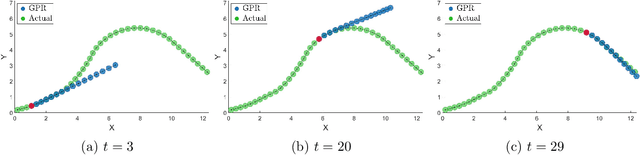
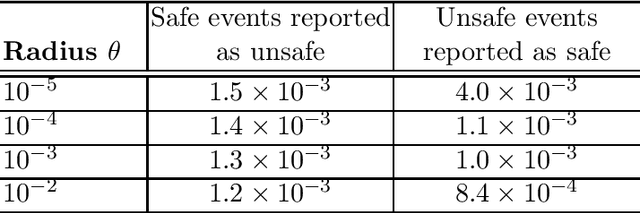
This paper proposes a novel safety specification tool, called the distributionally robust risk map (DR-risk map), for a mobile robot operating in a learning-enabled environment. Given the robot's position, the map aims to reliably assess the conditional value-at-risk (CVaR) of collision with obstacles whose movements are inferred by Gaussian process regression (GPR). Unfortunately, the inferred distribution is subject to errors, making it difficult to accurately evaluate the CVaR of collision. To overcome this challenge, this tool measures the risk under the worst-case distribution in a so-called ambiguity set that characterizes allowable distribution errors. To resolve the infinite-dimensionality issue inherent in the construction of the DR-risk map, we derive a tractable semidefinite programming formulation that provides an upper bound of the risk, exploiting techniques from modern distributionally robust optimization. As a concrete application for motion planning, a distributionally robust RRT* algorithm is considered using the risk map that addresses distribution errors caused by GPR. Furthermore, a motion control method is devised using the DR-risk map in a learning-based model predictive control (MPC) formulation. In particular, a neural network approximation of the risk map is proposed to reduce the computational cost in solving the MPC problem. The performance and utility of the proposed risk map are demonstrated through simulation studies that show its ability to ensure the safety of mobile robots despite learning errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge