Risk-Aware Wasserstein Distributionally Robust Control of Vessels in Natural Waterways

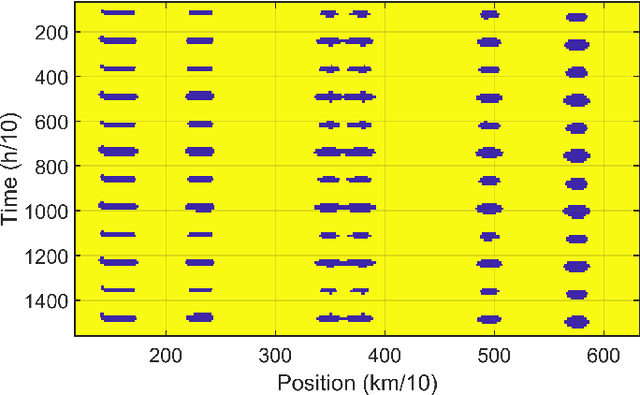
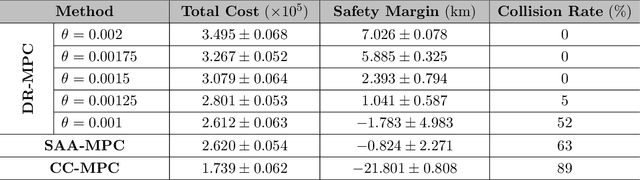
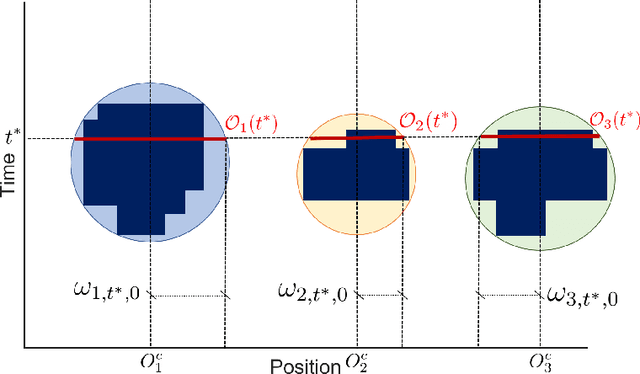
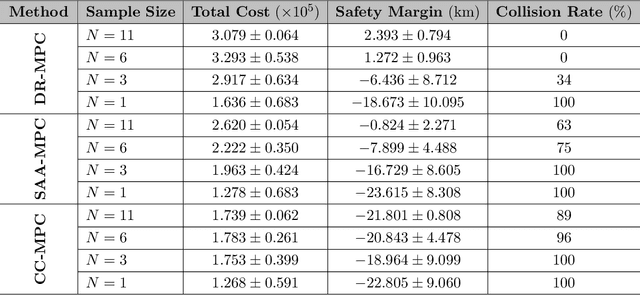
In the realm of maritime transportation, autonomous vessel navigation in natural inland waterways faces persistent challenges due to unpredictable natural factors. Existing scheduling algorithms fall short in handling these uncertainties, compromising both safety and efficiency. Moreover, these algorithms are primarily designed for non-autonomous vessels, leading to labor-intensive operations vulnerable to human error. To address these issues, this study proposes a risk-aware motion control approach for vessels that accounts for the dynamic and uncertain nature of tide islands in a distributionally robust manner. Specifically, a model predictive control method is employed to follow the reference trajectory in the time-space map while incorporating a risk constraint to prevent grounding accidents. To address uncertainties in tide islands, a novel modeling technique represents them as stochastic polytopes. Additionally, potential inaccuracies in waterway depth are addressed through a risk constraint that considers the worst-case uncertainty distribution within a Wasserstein ambiguity set around the empirical distribution. Using sensor data collected in the Guadalquivir River, we empirically demonstrate the performance of the proposed method through simulations on a vessel. As a result, the vessel successfully navigates the waterway while avoiding grounding accidents, even with a limited dataset of observations. This stands in contrast to existing non-robust controllers, highlighting the robustness and practical applicability of the proposed approach.

Infusing model predictive control into meta-reinforcement learning for mobile robots in dynamic environments

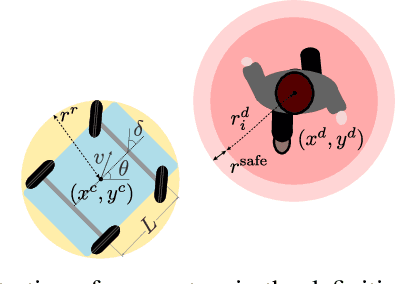
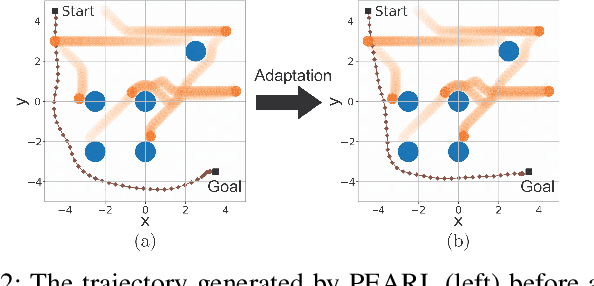
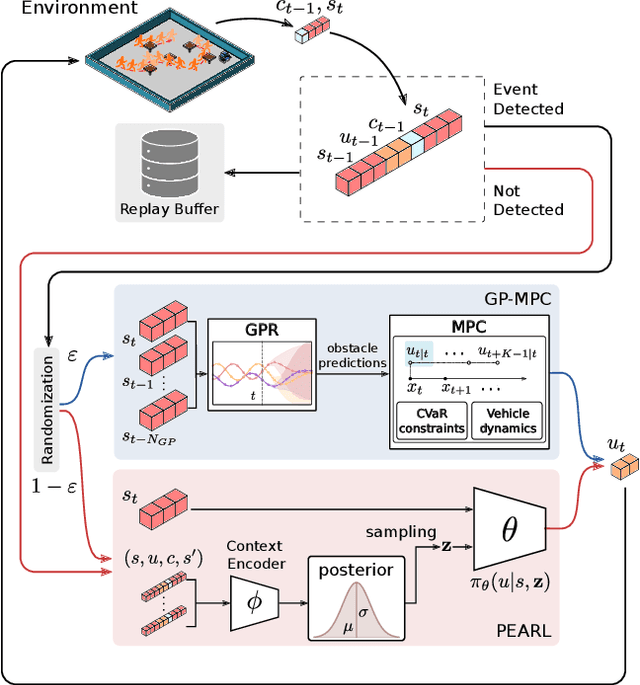
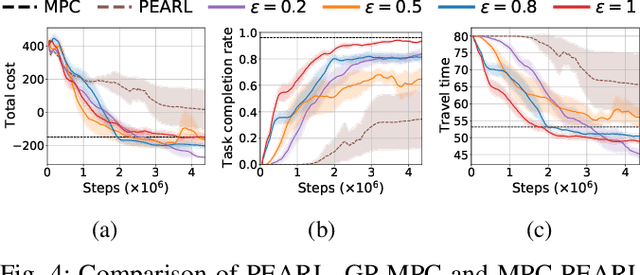
The successful operation of mobile robots requires them to rapidly adapt to environmental changes. Toward developing an adaptive decision-making tool for mobile robots, we propose combining meta-reinforcement learning (meta-RL) with model predictive control (MPC). The key idea of our method is to switch between a meta-learned policy and an MPC controller in an event-triggered fashion. Our method uses an off-policy meta-RL algorithm as a baseline to train a policy using transition samples generated by MPC. The MPC module of our algorithm is carefully designed to infer the movements of obstacles via Gaussian process regression (GPR) and to avoid collisions via conditional value-at-risk (CVaR) constraints. Due to its design, our method benefits from the two complementary tools. First, high-performance action samples generated by the MPC controller enhance the learning performance and stability of the meta-RL algorithm. Second, through the use of the meta-learned policy, the MPC controller is infrequently activated, thereby significantly reducing computation time. The results of our simulations on a restaurant service robot show that our algorithm outperforms both of the baseline methods.

Distributionally robust risk map for learning-based motion planning and control: A semidefinite programming approach

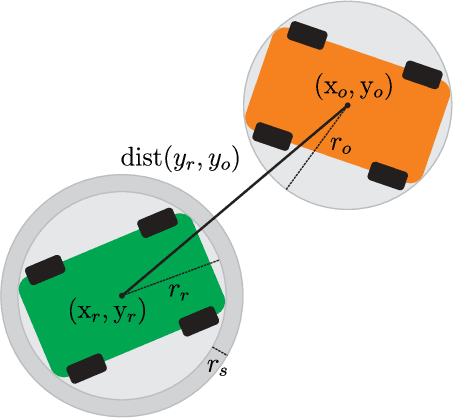
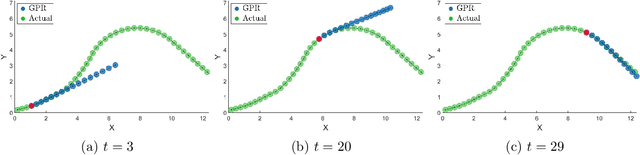
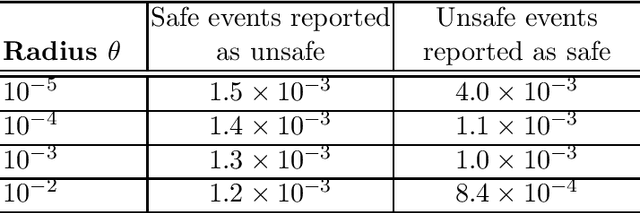
This paper proposes a novel safety specification tool, called the distributionally robust risk map (DR-risk map), for a mobile robot operating in a learning-enabled environment. Given the robot's position, the map aims to reliably assess the conditional value-at-risk (CVaR) of collision with obstacles whose movements are inferred by Gaussian process regression (GPR). Unfortunately, the inferred distribution is subject to errors, making it difficult to accurately evaluate the CVaR of collision. To overcome this challenge, this tool measures the risk under the worst-case distribution in a so-called ambiguity set that characterizes allowable distribution errors. To resolve the infinite-dimensionality issue inherent in the construction of the DR-risk map, we derive a tractable semidefinite programming formulation that provides an upper bound of the risk, exploiting techniques from modern distributionally robust optimization. As a concrete application for motion planning, a distributionally robust RRT* algorithm is considered using the risk map that addresses distribution errors caused by GPR. Furthermore, a motion control method is devised using the DR-risk map in a learning-based model predictive control (MPC) formulation. In particular, a neural network approximation of the risk map is proposed to reduce the computational cost in solving the MPC problem. The performance and utility of the proposed risk map are demonstrated through simulation studies that show its ability to ensure the safety of mobile robots despite learning errors.

Learning-based distributionally robust motion control with Gaussian processes

Safety is a critical issue in learning-based robotic and autonomous systems as learned information about their environments is often unreliable and inaccurate. In this paper, we propose a risk-aware motion control tool that is robust against errors in learned distributional information about obstacles moving with unknown dynamics. The salient feature of our model predictive control (MPC) method is its capability of limiting the risk of unsafety even when the true distribution deviates from the distribution estimated by Gaussian process (GP) regression, within an ambiguity set. Unfortunately, the distributionally robust MPC problem with GP is intractable because the worst-case risk constraint involves an infinite-dimensional optimization problem over the ambiguity set. To remove the infinite-dimensionality issue, we develop a systematic reformulation approach exploiting modern distributionally robust optimization techniques. The performance and utility of our method are demonstrated through simulations using a nonlinear car-like vehicle model for autonomous driving.

Wasserstein Distributionally Robust Motion Control for Collision Avoidance Using Conditional Value-at-Risk

In this paper, a risk-aware motion control scheme is considered for mobile robots to avoid randomly moving obstacles when the true probability distribution of uncertainty is unknown. We propose a novel model predictive control (MPC) method for limiting the risk of unsafety even when the true distribution of the obstacles' movements deviates, within an ambiguity set, from the empirical distribution obtained using a limited amount of sample data. By choosing the ambiguity set as a statistical ball with its radius measured by the Wasserstein metric, we achieve a probabilistic guarantee of the out-of-sample risk, evaluated using new sample data generated independently of the training data. To resolve the infinite-dimensionality issue inherent in the distributionally robust MPC problem, we reformulate it as a finite-dimensional nonlinear program using modern distributionally robust optimization techniques based on the Kantorovich duality principle. To find a globally optimal solution in the case of affine dynamics and output equations, a spatial branch-and-bound algorithm is designed using McCormick relaxation. The performance of the proposed method is demonstrated and analyzed through simulation studies using a nonlinear car-like vehicle model and a linearized quadrotor model.