Training Wasserstein GANs without gradient penalties
Paper and Code
Oct 27, 2021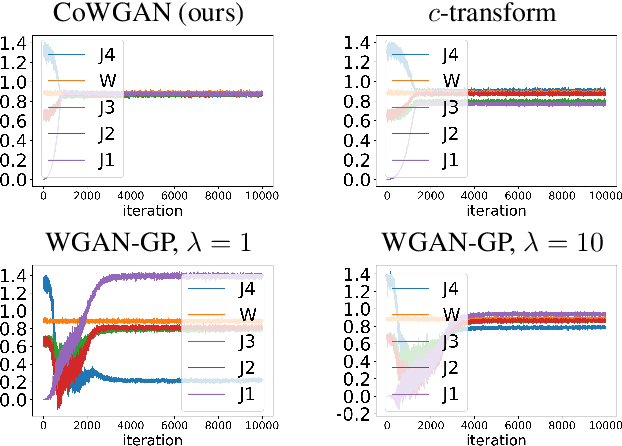

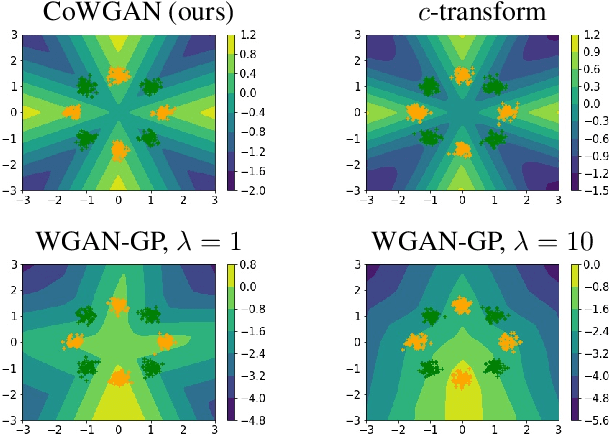
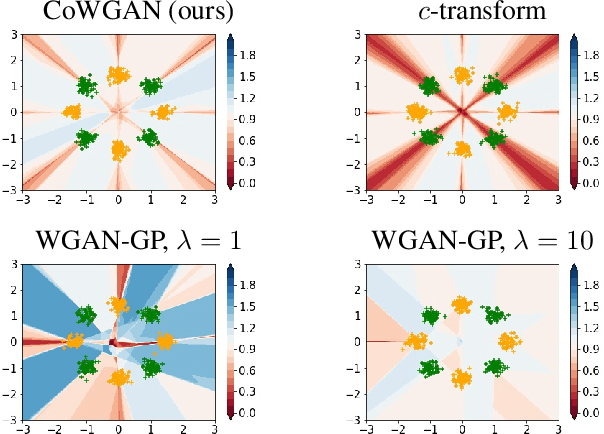
We propose a stable method to train Wasserstein generative adversarial networks. In order to enhance stability, we consider two objective functions using the $c$-transform based on Kantorovich duality which arises in the theory of optimal transport. We experimentally show that this algorithm can effectively enforce the Lipschitz constraint on the discriminator while other standard methods fail to do so. As a consequence, our method yields an accurate estimation for the optimal discriminator and also for the Wasserstein distance between the true distribution and the generated one. Our method requires no gradient penalties nor corresponding hyperparameter tuning and is computationally more efficient than other methods. At the same time, it yields competitive generators of synthetic images based on the MNIST, F-MNIST, and CIFAR-10 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge