Hamilton-Jacobi Based Policy-Iteration via Deep Operator Learning

The framework of deep operator network (DeepONet) has been widely exploited thanks to its capability of solving high dimensional partial differential equations. In this paper, we incorporate DeepONet with a recently developed policy iteration scheme to numerically solve optimal control problems and the corresponding Hamilton--Jacobi--Bellman (HJB) equations. A notable feature of our approach is that once the neural network is trained, the solution to the optimal control problem and HJB equations with different terminal functions can be inferred quickly thanks to the unique feature of operator learning. Furthermore, a quantitative analysis of the accuracy of the algorithm is carried out via comparison principles of viscosity solutions. The effectiveness of the method is verified with various examples, including 10-dimensional linear quadratic regulator problems (LQRs).

MonoPatchNeRF: Improving Neural Radiance Fields with Patch-based Monocular Guidance

The latest regularized Neural Radiance Field (NeRF) approaches produce poor geometry and view extrapolation for multiview stereo (MVS) benchmarks such as ETH3D. In this paper, we aim to create 3D models that provide accurate geometry and view synthesis, partially closing the large geometric performance gap between NeRF and traditional MVS methods. We propose a patch-based approach that effectively leverages monocular surface normal and relative depth predictions. The patch-based ray sampling also enables the appearance regularization of normalized cross-correlation (NCC) and structural similarity (SSIM) between randomly sampled virtual and training views. We further show that "density restrictions" based on sparse structure-from-motion points can help greatly improve geometric accuracy with a slight drop in novel view synthesis metrics. Our experiments show 4x the performance of RegNeRF and 8x that of FreeNeRF on average F1@2cm for ETH3D MVS benchmark, suggesting a fruitful research direction to improve the geometric accuracy of NeRF-based models, and sheds light on a potential future approach to enable NeRF-based optimization to eventually outperform traditional MVS.

Learning time-dependent PDE via graph neural networks and deep operator network for robust accuracy on irregular grids

Scientific computing using deep learning has seen significant advancements in recent years. There has been growing interest in models that learn the operator from the parameters of a partial differential equation (PDE) to the corresponding solutions. Deep Operator Network (DeepONet) and Fourier Neural operator, among other models, have been designed with structures suitable for handling functions as inputs and outputs, enabling real-time predictions as surrogate models for solution operators. There has also been significant progress in the research on surrogate models based on graph neural networks (GNNs), specifically targeting the dynamics in time-dependent PDEs. In this paper, we propose GraphDeepONet, an autoregressive model based on GNNs, to effectively adapt DeepONet, which is well-known for successful operator learning. GraphDeepONet exhibits robust accuracy in predicting solutions compared to existing GNN-based PDE solver models. It maintains consistent performance even on irregular grids, leveraging the advantages inherited from DeepONet and enabling predictions on arbitrary grids. Additionally, unlike traditional DeepONet and its variants, GraphDeepONet enables time extrapolation for time-dependent PDE solutions. We also provide theoretical analysis of the universal approximation capability of GraphDeepONet in approximating continuous operators across arbitrary time intervals.

Region-Based Representations Revisited

We investigate whether region-based representations are effective for recognition. Regions were once a mainstay in recognition approaches, but pixel and patch-based features are now used almost exclusively. We show that recent class-agnostic segmenters like SAM can be effectively combined with strong unsupervised representations like DINOv2 and used for a wide variety of tasks, including semantic segmentation, object-based image retrieval, and multi-image analysis. Once the masks and features are extracted, these representations, even with linear decoders, enable competitive performance, making them well suited to applications that require custom queries. The compactness of the representation also makes it well-suited to video analysis and other problems requiring inference across many images.

HyperDeepONet: learning operator with complex target function space using the limited resources via hypernetwork

Fast and accurate predictions for complex physical dynamics are a significant challenge across various applications. Real-time prediction on resource-constrained hardware is even more crucial in real-world problems. The deep operator network (DeepONet) has recently been proposed as a framework for learning nonlinear mappings between function spaces. However, the DeepONet requires many parameters and has a high computational cost when learning operators, particularly those with complex (discontinuous or non-smooth) target functions. This study proposes HyperDeepONet, which uses the expressive power of the hypernetwork to enable the learning of a complex operator with a smaller set of parameters. The DeepONet and its variant models can be thought of as a method of injecting the input function information into the target function. From this perspective, these models can be viewed as a particular case of HyperDeepONet. We analyze the complexity of DeepONet and conclude that HyperDeepONet needs relatively lower complexity to obtain the desired accuracy for operator learning. HyperDeepONet successfully learned various operators with fewer computational resources compared to other benchmarks.

Finite Element Operator Network for Solving Parametric PDEs

Partial differential equations (PDEs) underlie our understanding and prediction of natural phenomena across numerous fields, including physics, engineering, and finance. However, solving parametric PDEs is a complex task that necessitates efficient numerical methods. In this paper, we propose a novel approach for solving parametric PDEs using a Finite Element Operator Network (FEONet). Our proposed method leverages the power of deep learning in conjunction with traditional numerical methods, specifically the finite element method, to solve parametric PDEs in the absence of any paired input-output training data. We demonstrate the effectiveness of our approach on several benchmark problems and show that it outperforms existing state-of-the-art methods in terms of accuracy, generalization, and computational flexibility. Our FEONet framework shows potential for application in various fields where PDEs play a crucial role in modeling complex domains with diverse boundary conditions and singular behavior. Furthermore, we provide theoretical convergence analysis to support our approach, utilizing finite element approximation in numerical analysis.

Sparse SPN: Depth Completion from Sparse Keypoints

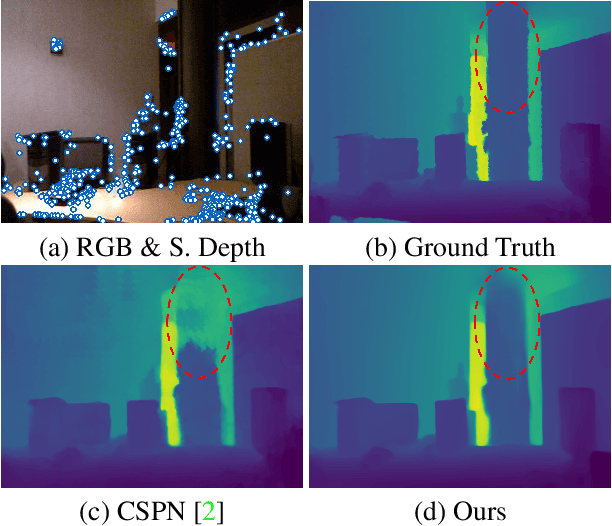
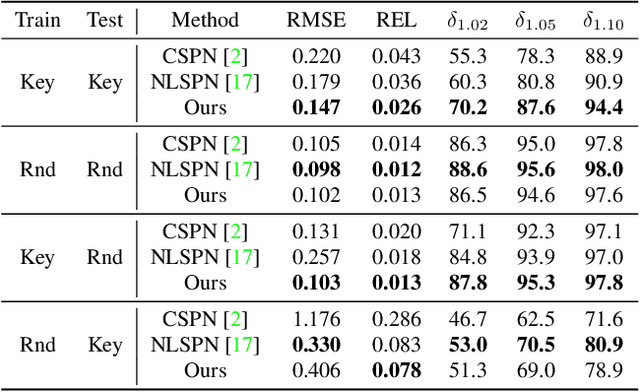
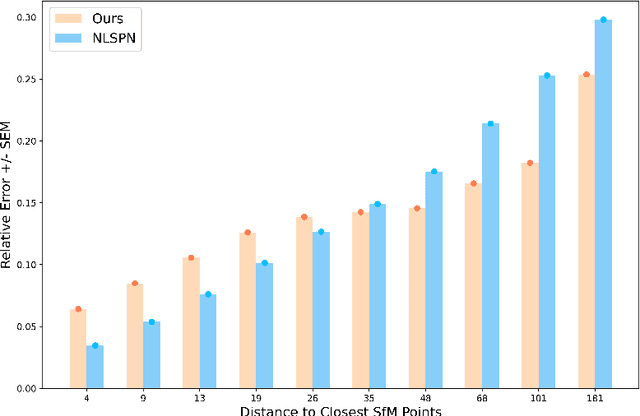
Our long term goal is to use image-based depth completion to quickly create 3D models from sparse point clouds, e.g. from SfM or SLAM. Much progress has been made in depth completion. However, most current works assume well distributed samples of known depth, e.g. Lidar or random uniform sampling, and perform poorly on uneven samples, such as from keypoints, due to the large unsampled regions. To address this problem, we extend CSPN with multiscale prediction and a dilated kernel, leading to much better completion of keypoint-sampled depth. We also show that a model trained on NYUv2 creates surprisingly good point clouds on ETH3D by completing sparse SfM points.

QFF: Quantized Fourier Features for Neural Field Representations

Multilayer perceptrons (MLPs) learn high frequencies slowly. Recent approaches encode features in spatial bins to improve speed of learning details, but at the cost of larger model size and loss of continuity. Instead, we propose to encode features in bins of Fourier features that are commonly used for positional encoding. We call these Quantized Fourier Features (QFF). As a naturally multiresolution and periodic representation, our experiments show that using QFF can result in smaller model size, faster training, and better quality outputs for several applications, including Neural Image Representations (NIR), Neural Radiance Field (NeRF) and Signed Distance Function (SDF) modeling. QFF are easy to code, fast to compute, and serve as a simple drop-in addition to many neural field representations.

Deep PatchMatch MVS with Learned Patch Coplanarity, Geometric Consistency and Adaptive Pixel Sampling

Recent work in multi-view stereo (MVS) combines learnable photometric scores and regularization with PatchMatch-based optimization to achieve robust pixelwise estimates of depth, normals, and visibility. However, non-learning based methods still outperform for large scenes with sparse views, in part due to use of geometric consistency constraints and ability to optimize over many views at high resolution. In this paper, we build on learning-based approaches to improve photometric scores by learning patch coplanarity and encourage geometric consistency by learning a scaled photometric cost that can be combined with reprojection error. We also propose an adaptive pixel sampling strategy for candidate propagation that reduces memory to enable training on larger resolution with more views and a larger encoder. These modifications lead to 6-15% gains in accuracy and completeness on the challenging ETH3D benchmark, resulting in higher F1 performance than the widely used state-of-the-art non-learning approaches ACMM and ACMP.

opPINN: Physics-Informed Neural Network with operator learning to approximate solutions to the Fokker-Planck-Landau equation

We propose a hybrid framework opPINN: physics-informed neural network (PINN) with operator learning for approximating the solution to the Fokker-Planck-Landau (FPL) equation. The opPINN framework is divided into two steps: Step 1 and Step 2. After the operator surrogate models are trained during Step 1, PINN can effectively approximate the solution to the FPL equation during Step 2 by using the pre-trained surrogate models. The operator surrogate models greatly reduce the computational cost and boost PINN by approximating the complex Landau collision integral in the FPL equation. The operator surrogate models can also be combined with the traditional numerical schemes. It provides a high efficiency in computational time when the number of velocity modes becomes larger. Using the opPINN framework, we provide the neural network solutions for the FPL equation under the various types of initial conditions, and interaction models in two and three dimensions. Furthermore, based on the theoretical properties of the FPL equation, we show that the approximated neural network solution converges to the a priori classical solution of the FPL equation as the pre-defined loss function is reduced.