Estimating the Distribution of Parameters in Differential Equations with Repeated Cross-Sectional Data

Differential equations are pivotal in modeling and understanding the dynamics of various systems, offering insights into their future states through parameter estimation fitted to time series data. In fields such as economy, politics, and biology, the observation data points in the time series are often independently obtained (i.e., Repeated Cross-Sectional (RCS) data). With RCS data, we found that traditional methods for parameter estimation in differential equations, such as using mean values of time trajectories or Gaussian Process-based trajectory generation, have limitations in estimating the shape of parameter distributions, often leading to a significant loss of data information. To address this issue, we introduce a novel method, Estimation of Parameter Distribution (EPD), providing accurate distribution of parameters without loss of data information. EPD operates in three main steps: generating synthetic time trajectories by randomly selecting observed values at each time point, estimating parameters of a differential equation that minimize the discrepancy between these trajectories and the true solution of the equation, and selecting the parameters depending on the scale of discrepancy. We then evaluated the performance of EPD across several models, including exponential growth, logistic population models, and target cell-limited models with delayed virus production, demonstrating its superiority in capturing the shape of parameter distributions. Furthermore, we applied EPD to real-world datasets, capturing various shapes of parameter distributions rather than a normal distribution. These results effectively address the heterogeneity within systems, marking a substantial progression in accurately modeling systems using RCS data.

Sobolev Training for Operator Learning

This study investigates the impact of Sobolev Training on operator learning frameworks for improving model performance. Our research reveals that integrating derivative information into the loss function enhances the training process, and we propose a novel framework to approximate derivatives on irregular meshes in operator learning. Our findings are supported by both experimental evidence and theoretical analysis. This demonstrates the effectiveness of Sobolev Training in approximating the solution operators between infinite-dimensional spaces.

Learning time-dependent PDE via graph neural networks and deep operator network for robust accuracy on irregular grids

Scientific computing using deep learning has seen significant advancements in recent years. There has been growing interest in models that learn the operator from the parameters of a partial differential equation (PDE) to the corresponding solutions. Deep Operator Network (DeepONet) and Fourier Neural operator, among other models, have been designed with structures suitable for handling functions as inputs and outputs, enabling real-time predictions as surrogate models for solution operators. There has also been significant progress in the research on surrogate models based on graph neural networks (GNNs), specifically targeting the dynamics in time-dependent PDEs. In this paper, we propose GraphDeepONet, an autoregressive model based on GNNs, to effectively adapt DeepONet, which is well-known for successful operator learning. GraphDeepONet exhibits robust accuracy in predicting solutions compared to existing GNN-based PDE solver models. It maintains consistent performance even on irregular grids, leveraging the advantages inherited from DeepONet and enabling predictions on arbitrary grids. Additionally, unlike traditional DeepONet and its variants, GraphDeepONet enables time extrapolation for time-dependent PDE solutions. We also provide theoretical analysis of the universal approximation capability of GraphDeepONet in approximating continuous operators across arbitrary time intervals.

HyperDeepONet: learning operator with complex target function space using the limited resources via hypernetwork

Fast and accurate predictions for complex physical dynamics are a significant challenge across various applications. Real-time prediction on resource-constrained hardware is even more crucial in real-world problems. The deep operator network (DeepONet) has recently been proposed as a framework for learning nonlinear mappings between function spaces. However, the DeepONet requires many parameters and has a high computational cost when learning operators, particularly those with complex (discontinuous or non-smooth) target functions. This study proposes HyperDeepONet, which uses the expressive power of the hypernetwork to enable the learning of a complex operator with a smaller set of parameters. The DeepONet and its variant models can be thought of as a method of injecting the input function information into the target function. From this perspective, these models can be viewed as a particular case of HyperDeepONet. We analyze the complexity of DeepONet and conclude that HyperDeepONet needs relatively lower complexity to obtain the desired accuracy for operator learning. HyperDeepONet successfully learned various operators with fewer computational resources compared to other benchmarks.

opPINN: Physics-Informed Neural Network with operator learning to approximate solutions to the Fokker-Planck-Landau equation

We propose a hybrid framework opPINN: physics-informed neural network (PINN) with operator learning for approximating the solution to the Fokker-Planck-Landau (FPL) equation. The opPINN framework is divided into two steps: Step 1 and Step 2. After the operator surrogate models are trained during Step 1, PINN can effectively approximate the solution to the FPL equation during Step 2 by using the pre-trained surrogate models. The operator surrogate models greatly reduce the computational cost and boost PINN by approximating the complex Landau collision integral in the FPL equation. The operator surrogate models can also be combined with the traditional numerical schemes. It provides a high efficiency in computational time when the number of velocity modes becomes larger. Using the opPINN framework, we provide the neural network solutions for the FPL equation under the various types of initial conditions, and interaction models in two and three dimensions. Furthermore, based on the theoretical properties of the FPL equation, we show that the approximated neural network solution converges to the a priori classical solution of the FPL equation as the pre-defined loss function is reduced.

AL-PINNs: Augmented Lagrangian relaxation method for Physics-Informed Neural Networks

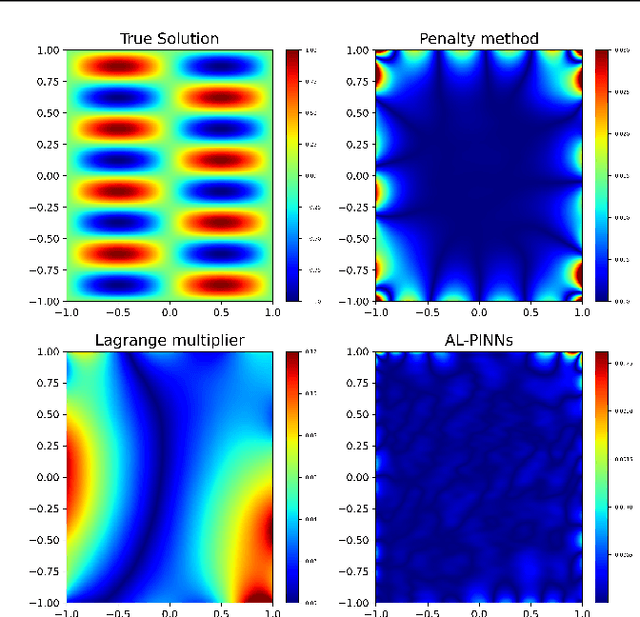
Physics-Informed Neural Networks (PINNs) has become a prominent application of deep learning in scientific computation, as it is a powerful approximator of solutions to nonlinear partial differential equations (PDEs). There have been numerous attempts to facilitate the training process of PINNs by adjusting the weight of each component of the loss function, called adaptive loss balancing algorithms. In this paper, we propose an Augmented Lagrangian relaxation method for PINNs (AL-PINNs). We treat the initial and boundary conditions as constraints for the optimization problem of the PDE residual. By employing Augmented Lagrangian relaxation, the constrained optimization problem becomes a sequential max-min problem so that the learnable parameters $\lambda$'s adaptively balance each loss component. Our theoretical analysis reveals that the sequence of minimizers of the proposed loss functions converges to an actual solution for the Helmholtz, viscous Burgers, and Klein--Gordon equations. We demonstrate through various numerical experiments that AL-PINNs yields a much smaller relative error compared with that of state-of-the-art adaptive loss balancing algorithms.

Pseudo-Differential Integral Operator for Learning Solution Operators of Partial Differential Equations

Learning mapping between two function spaces has attracted considerable research attention. However, learning the solution operator of partial differential equations (PDEs) remains a challenge in scientific computing. Therefore, in this study, we propose a novel pseudo-differential integral operator (PDIO) inspired by a pseudo-differential operator, which is a generalization of a differential operator and characterized by a certain symbol. We parameterize the symbol by using a neural network and show that the neural-network-based symbol is contained in a smooth symbol class. Subsequently, we prove that the PDIO is a bounded linear operator, and thus is continuous in the Sobolev space. We combine the PDIO with the neural operator to develop a pseudo-differential neural operator (PDNO) to learn the nonlinear solution operator of PDEs. We experimentally validate the effectiveness of the proposed model by using Burgers' equation, Darcy flow, and the Navier-Stokes equation. The results reveal that the proposed PDNO outperforms the existing neural operator approaches in most experiments.

Solving PDE-constrained Control Problems using Operator Learning

The modeling and control of complex physical dynamics are essential in real-world problems. We propose a novel framework that is generally applicable to solving PDE-constrained optimal control problems by introducing surrogate models for PDE solution operators with special regularizers. The procedure of the proposed framework is divided into two phases: solution operator learning for PDE constraints (Phase 1) and searching for optimal control (Phase 2). Once the surrogate model is trained in Phase 1, the optimal control can be inferred in Phase 2 without intensive computations. Our framework can be applied to both data-driven and data-free cases. We demonstrate the successful application of our method to various optimal control problems for different control variables with diverse PDE constraints from the Poisson equation to Burgers' equation.

Development of patients triage algorithm from nationwide COVID-19 registry data based on machine learning

Prompt severity assessment model of confirmed patients who were infected with infectious diseases could enable efficient diagnosis and alleviate the burden on the medical system. This paper provides the development processes of the severity assessment model using machine learning techniques and its application on SARS-CoV-2 patients. Here, we highlight that our model only requires basic patients' basic personal data, allowing for them to judge their own severity. We selected the boosting-based decision tree model as a classifier and interpreted mortality as a probability score after modeling. Specifically, hyperparameters that determine the structure of the tree model were tuned using the Bayesian optimization technique without any knowledge of medical information. As a result, we measured model performance and identified the variables affecting the severity through the model. Finally, we aim to establish a medical system that allows patients to check their own severity and informs them to visit the appropriate clinic center based on the past treatment details of other patients with similar severity.

Lagrangian dual framework for conservative neural network solutions of kinetic equations

In this paper, we propose a novel conservative formulation for solving kinetic equations via neural networks. More precisely, we formulate the learning problem as a constrained optimization problem with constraints that represent the physical conservation laws. The constraints are relaxed toward the residual loss function by the Lagrangian duality. By imposing physical conservation properties of the solution as constraints of the learning problem, we demonstrate far more accurate approximations of the solutions in terms of errors and the conservation laws, for the kinetic Fokker-Planck equation and the homogeneous Boltzmann equation.