Physics-Informed Deep Inverse Operator Networks for Solving PDE Inverse Problems

Inverse problems involving partial differential equations (PDEs) can be seen as discovering a mapping from measurement data to unknown quantities, often framed within an operator learning approach. However, existing methods typically rely on large amounts of labeled training data, which is impractical for most real-world applications. Moreover, these supervised models may fail to capture the underlying physical principles accurately. To address these limitations, we propose a novel architecture called Physics-Informed Deep Inverse Operator Networks (PI-DIONs), which can learn the solution operator of PDE-based inverse problems without labeled training data. We extend the stability estimates established in the inverse problem literature to the operator learning framework, thereby providing a robust theoretical foundation for our method. These estimates guarantee that the proposed model, trained on a finite sample and grid, generalizes effectively across the entire domain and function space. Extensive experiments are conducted to demonstrate that PI-DIONs can effectively and accurately learn the solution operators of the inverse problems without the need for labeled data.

AL-PINNs: Augmented Lagrangian relaxation method for Physics-Informed Neural Networks

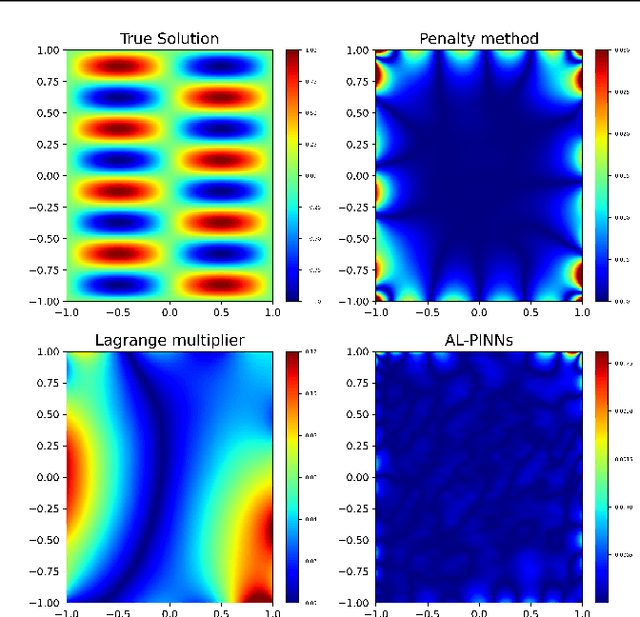
Physics-Informed Neural Networks (PINNs) has become a prominent application of deep learning in scientific computation, as it is a powerful approximator of solutions to nonlinear partial differential equations (PDEs). There have been numerous attempts to facilitate the training process of PINNs by adjusting the weight of each component of the loss function, called adaptive loss balancing algorithms. In this paper, we propose an Augmented Lagrangian relaxation method for PINNs (AL-PINNs). We treat the initial and boundary conditions as constraints for the optimization problem of the PDE residual. By employing Augmented Lagrangian relaxation, the constrained optimization problem becomes a sequential max-min problem so that the learnable parameters $\lambda$'s adaptively balance each loss component. Our theoretical analysis reveals that the sequence of minimizers of the proposed loss functions converges to an actual solution for the Helmholtz, viscous Burgers, and Klein--Gordon equations. We demonstrate through various numerical experiments that AL-PINNs yields a much smaller relative error compared with that of state-of-the-art adaptive loss balancing algorithms.

Lagrangian dual framework for conservative neural network solutions of kinetic equations

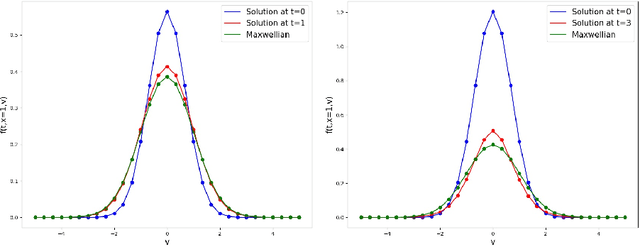
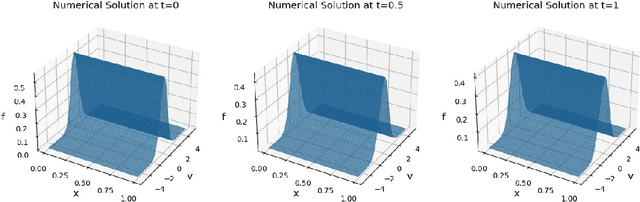
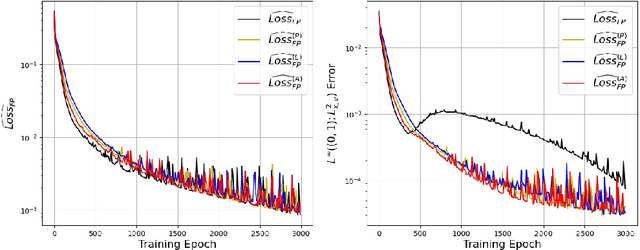
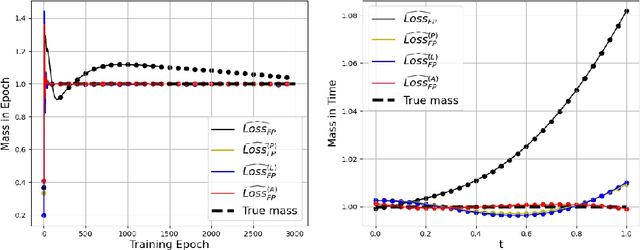
In this paper, we propose a novel conservative formulation for solving kinetic equations via neural networks. More precisely, we formulate the learning problem as a constrained optimization problem with constraints that represent the physical conservation laws. The constraints are relaxed toward the residual loss function by the Lagrangian duality. By imposing physical conservation properties of the solution as constraints of the learning problem, we demonstrate far more accurate approximations of the solutions in terms of errors and the conservation laws, for the kinetic Fokker-Planck equation and the homogeneous Boltzmann equation.

Deep Neural Network Approach to Forward-Inverse Problems

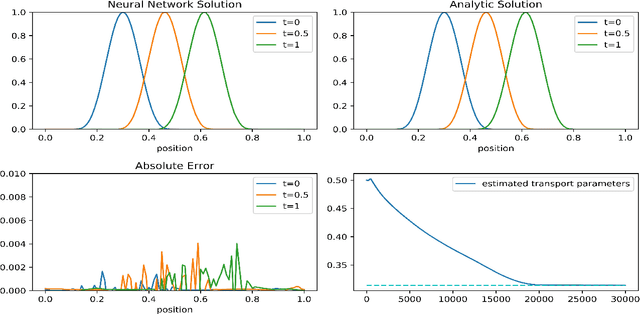
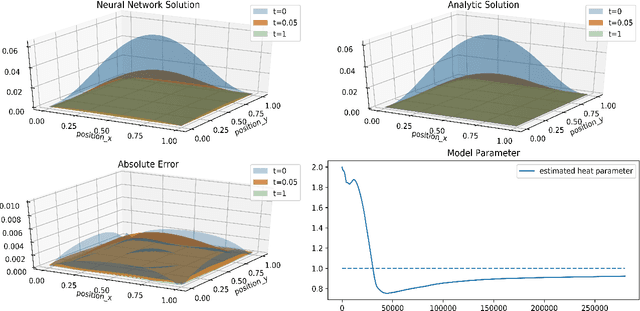
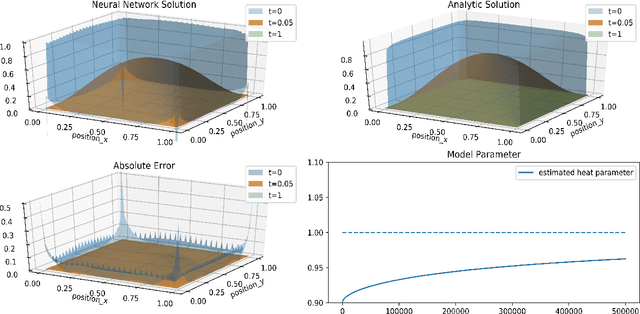
In this paper, we construct approximated solutions of Differential Equations (DEs) using the Deep Neural Network (DNN). Furthermore, we present an architecture that includes the process of finding model parameters through experimental data, the inverse problem. That is, we provide a unified framework of DNN architecture that approximates an analytic solution and its model parameters simultaneously. The architecture consists of a feed forward DNN with non-linear activation functions depending on DEs, automatic differentiation, reduction of order, and gradient based optimization method. We also prove theoretically that the proposed DNN solution converges to an analytic solution in a suitable function space for fundamental DEs. Finally, we perform numerical experiments to validate the robustness of our simplistic DNN architecture for 1D transport equation, 2D heat equation, 2D wave equation, and the Lotka-Volterra system.