Physics-Informed Deep Inverse Operator Networks for Solving PDE Inverse Problems

Inverse problems involving partial differential equations (PDEs) can be seen as discovering a mapping from measurement data to unknown quantities, often framed within an operator learning approach. However, existing methods typically rely on large amounts of labeled training data, which is impractical for most real-world applications. Moreover, these supervised models may fail to capture the underlying physical principles accurately. To address these limitations, we propose a novel architecture called Physics-Informed Deep Inverse Operator Networks (PI-DIONs), which can learn the solution operator of PDE-based inverse problems without labeled training data. We extend the stability estimates established in the inverse problem literature to the operator learning framework, thereby providing a robust theoretical foundation for our method. These estimates guarantee that the proposed model, trained on a finite sample and grid, generalizes effectively across the entire domain and function space. Extensive experiments are conducted to demonstrate that PI-DIONs can effectively and accurately learn the solution operators of the inverse problems without the need for labeled data.

Estimating the Distribution of Parameters in Differential Equations with Repeated Cross-Sectional Data

Differential equations are pivotal in modeling and understanding the dynamics of various systems, offering insights into their future states through parameter estimation fitted to time series data. In fields such as economy, politics, and biology, the observation data points in the time series are often independently obtained (i.e., Repeated Cross-Sectional (RCS) data). With RCS data, we found that traditional methods for parameter estimation in differential equations, such as using mean values of time trajectories or Gaussian Process-based trajectory generation, have limitations in estimating the shape of parameter distributions, often leading to a significant loss of data information. To address this issue, we introduce a novel method, Estimation of Parameter Distribution (EPD), providing accurate distribution of parameters without loss of data information. EPD operates in three main steps: generating synthetic time trajectories by randomly selecting observed values at each time point, estimating parameters of a differential equation that minimize the discrepancy between these trajectories and the true solution of the equation, and selecting the parameters depending on the scale of discrepancy. We then evaluated the performance of EPD across several models, including exponential growth, logistic population models, and target cell-limited models with delayed virus production, demonstrating its superiority in capturing the shape of parameter distributions. Furthermore, we applied EPD to real-world datasets, capturing various shapes of parameter distributions rather than a normal distribution. These results effectively address the heterogeneity within systems, marking a substantial progression in accurately modeling systems using RCS data.

Learning time-dependent PDE via graph neural networks and deep operator network for robust accuracy on irregular grids

Scientific computing using deep learning has seen significant advancements in recent years. There has been growing interest in models that learn the operator from the parameters of a partial differential equation (PDE) to the corresponding solutions. Deep Operator Network (DeepONet) and Fourier Neural operator, among other models, have been designed with structures suitable for handling functions as inputs and outputs, enabling real-time predictions as surrogate models for solution operators. There has also been significant progress in the research on surrogate models based on graph neural networks (GNNs), specifically targeting the dynamics in time-dependent PDEs. In this paper, we propose GraphDeepONet, an autoregressive model based on GNNs, to effectively adapt DeepONet, which is well-known for successful operator learning. GraphDeepONet exhibits robust accuracy in predicting solutions compared to existing GNN-based PDE solver models. It maintains consistent performance even on irregular grids, leveraging the advantages inherited from DeepONet and enabling predictions on arbitrary grids. Additionally, unlike traditional DeepONet and its variants, GraphDeepONet enables time extrapolation for time-dependent PDE solutions. We also provide theoretical analysis of the universal approximation capability of GraphDeepONet in approximating continuous operators across arbitrary time intervals.

HyperDeepONet: learning operator with complex target function space using the limited resources via hypernetwork

Fast and accurate predictions for complex physical dynamics are a significant challenge across various applications. Real-time prediction on resource-constrained hardware is even more crucial in real-world problems. The deep operator network (DeepONet) has recently been proposed as a framework for learning nonlinear mappings between function spaces. However, the DeepONet requires many parameters and has a high computational cost when learning operators, particularly those with complex (discontinuous or non-smooth) target functions. This study proposes HyperDeepONet, which uses the expressive power of the hypernetwork to enable the learning of a complex operator with a smaller set of parameters. The DeepONet and its variant models can be thought of as a method of injecting the input function information into the target function. From this perspective, these models can be viewed as a particular case of HyperDeepONet. We analyze the complexity of DeepONet and conclude that HyperDeepONet needs relatively lower complexity to obtain the desired accuracy for operator learning. HyperDeepONet successfully learned various operators with fewer computational resources compared to other benchmarks.

AL-PINNs: Augmented Lagrangian relaxation method for Physics-Informed Neural Networks

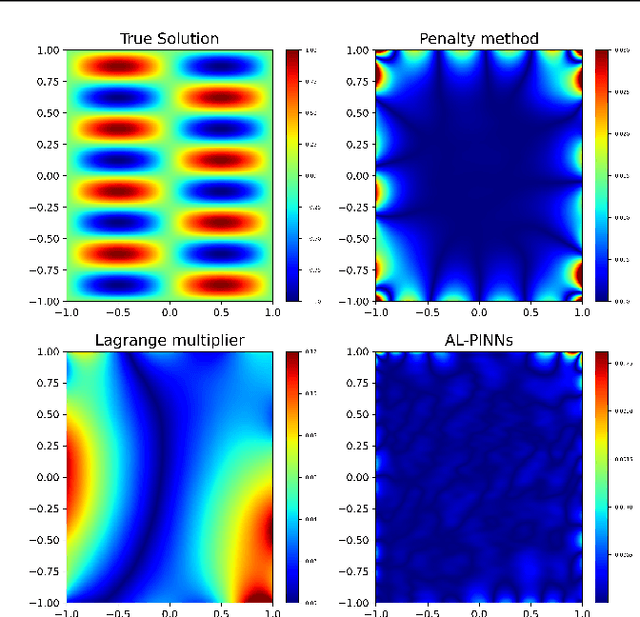
Physics-Informed Neural Networks (PINNs) has become a prominent application of deep learning in scientific computation, as it is a powerful approximator of solutions to nonlinear partial differential equations (PDEs). There have been numerous attempts to facilitate the training process of PINNs by adjusting the weight of each component of the loss function, called adaptive loss balancing algorithms. In this paper, we propose an Augmented Lagrangian relaxation method for PINNs (AL-PINNs). We treat the initial and boundary conditions as constraints for the optimization problem of the PDE residual. By employing Augmented Lagrangian relaxation, the constrained optimization problem becomes a sequential max-min problem so that the learnable parameters $\lambda$'s adaptively balance each loss component. Our theoretical analysis reveals that the sequence of minimizers of the proposed loss functions converges to an actual solution for the Helmholtz, viscous Burgers, and Klein--Gordon equations. We demonstrate through various numerical experiments that AL-PINNs yields a much smaller relative error compared with that of state-of-the-art adaptive loss balancing algorithms.