Estimation of System Parameters Including Repeated Cross-Sectional Data through Emulator-Informed Deep Generative Model

Differential equations (DEs) are crucial for modeling the evolution of natural or engineered systems. Traditionally, the parameters in DEs are adjusted to fit data from system observations. However, in fields such as politics, economics, and biology, available data are often independently collected at distinct time points from different subjects (i.e., repeated cross-sectional (RCS) data). Conventional optimization techniques struggle to accurately estimate DE parameters when RCS data exhibit various heterogeneities, leading to a significant loss of information. To address this issue, we propose a new estimation method called the emulator-informed deep-generative model (EIDGM), designed to handle RCS data. Specifically, EIDGM integrates a physics-informed neural network-based emulator that immediately generates DE solutions and a Wasserstein generative adversarial network-based parameter generator that can effectively mimic the RCS data. We evaluated EIDGM on exponential growth, logistic population models, and the Lorenz system, demonstrating its superior ability to accurately capture parameter distributions. Additionally, we applied EIDGM to an experimental dataset of Amyloid beta 40 and beta 42, successfully capturing diverse parameter distribution shapes. This shows that EIDGM can be applied to model a wide range of systems and extended to uncover the operating principles of systems based on limited data.

Estimating the Distribution of Parameters in Differential Equations with Repeated Cross-Sectional Data

Differential equations are pivotal in modeling and understanding the dynamics of various systems, offering insights into their future states through parameter estimation fitted to time series data. In fields such as economy, politics, and biology, the observation data points in the time series are often independently obtained (i.e., Repeated Cross-Sectional (RCS) data). With RCS data, we found that traditional methods for parameter estimation in differential equations, such as using mean values of time trajectories or Gaussian Process-based trajectory generation, have limitations in estimating the shape of parameter distributions, often leading to a significant loss of data information. To address this issue, we introduce a novel method, Estimation of Parameter Distribution (EPD), providing accurate distribution of parameters without loss of data information. EPD operates in three main steps: generating synthetic time trajectories by randomly selecting observed values at each time point, estimating parameters of a differential equation that minimize the discrepancy between these trajectories and the true solution of the equation, and selecting the parameters depending on the scale of discrepancy. We then evaluated the performance of EPD across several models, including exponential growth, logistic population models, and target cell-limited models with delayed virus production, demonstrating its superiority in capturing the shape of parameter distributions. Furthermore, we applied EPD to real-world datasets, capturing various shapes of parameter distributions rather than a normal distribution. These results effectively address the heterogeneity within systems, marking a substantial progression in accurately modeling systems using RCS data.

Development of patients triage algorithm from nationwide COVID-19 registry data based on machine learning

Prompt severity assessment model of confirmed patients who were infected with infectious diseases could enable efficient diagnosis and alleviate the burden on the medical system. This paper provides the development processes of the severity assessment model using machine learning techniques and its application on SARS-CoV-2 patients. Here, we highlight that our model only requires basic patients' basic personal data, allowing for them to judge their own severity. We selected the boosting-based decision tree model as a classifier and interpreted mortality as a probability score after modeling. Specifically, hyperparameters that determine the structure of the tree model were tuned using the Bayesian optimization technique without any knowledge of medical information. As a result, we measured model performance and identified the variables affecting the severity through the model. Finally, we aim to establish a medical system that allows patients to check their own severity and informs them to visit the appropriate clinic center based on the past treatment details of other patients with similar severity.

Trend to Equilibrium for the Kinetic Fokker-Planck Equation via the Neural Network Approach

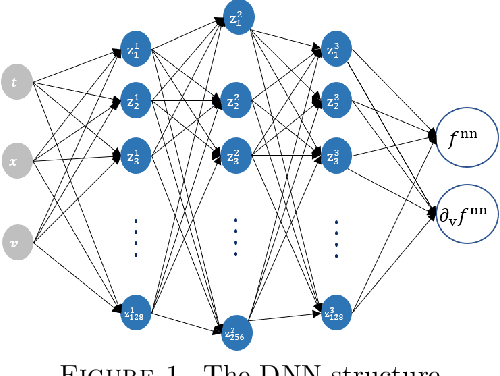
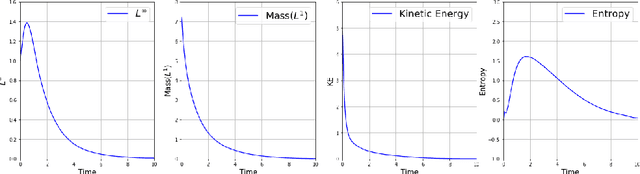
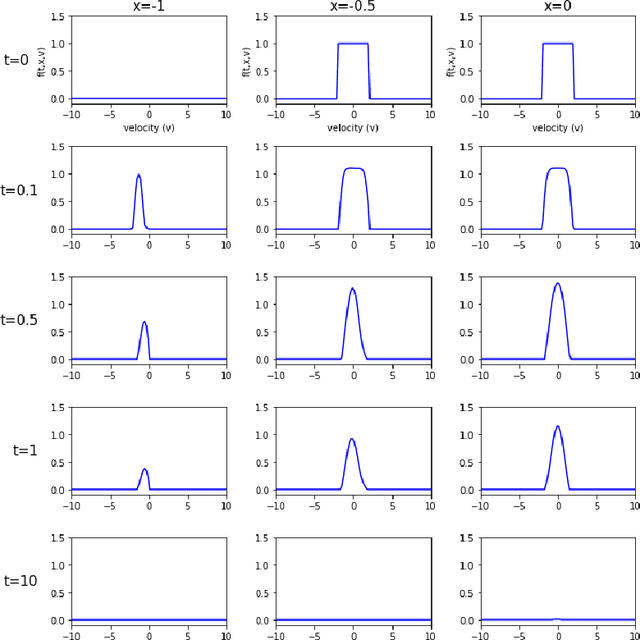
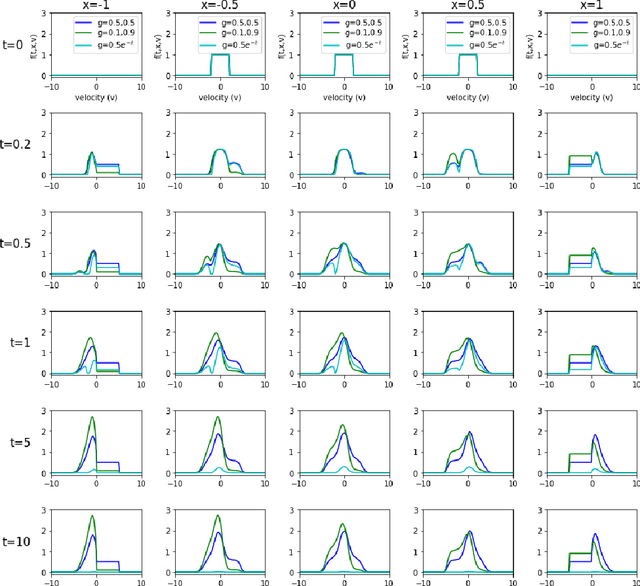
The issue of the relaxation to equilibrium has been at the core of the kinetic theory of rarefied gas dynamics. In the paper, we introduce the Deep Neural Network (DNN) approximated solutions to the kinetic Fokker-Planck equation in a bounded interval and study the large-time asymptotic behavior of the solutions and other physically relevant macroscopic quantities. We impose the varied types of boundary conditions including the inflow-type and the reflection-type boundaries as well as the varied diffusion and friction coefficients and study the boundary effects on the asymptotic behaviors. These include the predictions on the large-time behaviors of the pointwise values of the particle distribution and the macroscopic physical quantities including the total kinetic energy, the entropy, and the free energy. We also provide the theoretical supports for the pointwise convergence of the neural network solutions to the \textit{a priori} analytic solutions. We use the library \textit{PyTorch}, the activation function \textit{tanh} between layers, and the \textit{Adam} optimizer for the Deep Learning algorithm.

Deep Neural Network Approach to Forward-Inverse Problems

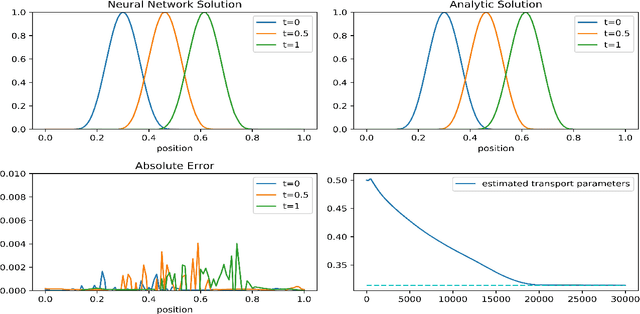
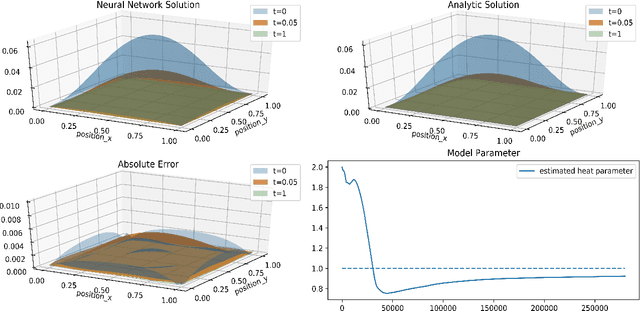
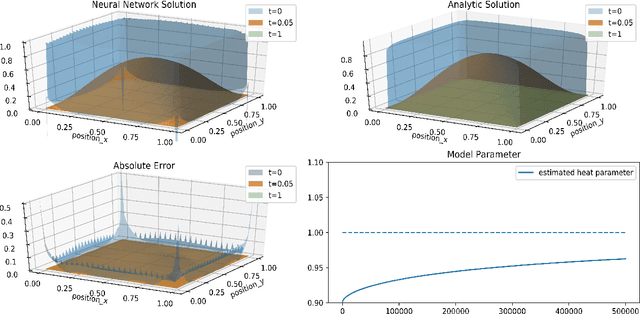
In this paper, we construct approximated solutions of Differential Equations (DEs) using the Deep Neural Network (DNN). Furthermore, we present an architecture that includes the process of finding model parameters through experimental data, the inverse problem. That is, we provide a unified framework of DNN architecture that approximates an analytic solution and its model parameters simultaneously. The architecture consists of a feed forward DNN with non-linear activation functions depending on DEs, automatic differentiation, reduction of order, and gradient based optimization method. We also prove theoretically that the proposed DNN solution converges to an analytic solution in a suitable function space for fundamental DEs. Finally, we perform numerical experiments to validate the robustness of our simplistic DNN architecture for 1D transport equation, 2D heat equation, 2D wave equation, and the Lotka-Volterra system.