The model reduction of the Vlasov-Poisson-Fokker-Planck system to the Poisson-Nernst-Planck system via the Deep Neural Network Approach

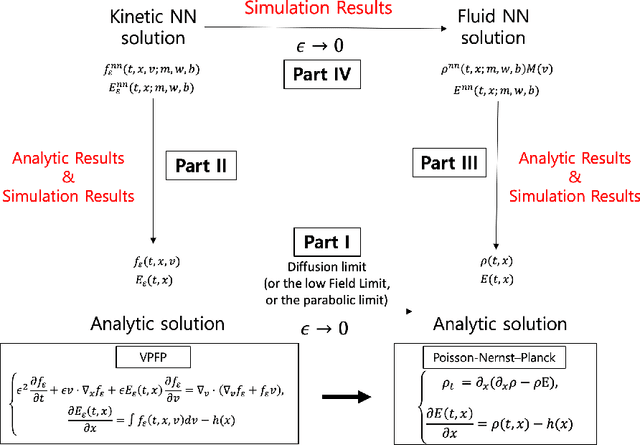
The model reduction of a mesoscopic kinetic dynamics to a macroscopic continuum dynamics has been one of the fundamental questions in mathematical physics since Hilbert's time. In this paper, we consider a diagram of the diffusion limit from the Vlasov-Poisson-Fokker-Planck (VPFP) system on a bounded interval with the specular reflection boundary condition to the Poisson-Nernst-Planck (PNP) system with the no-flux boundary condition. We provide a Deep Learning algorithm to simulate the VPFP system and the PNP system by computing the time-asymptotic behaviors of the solution and the physical quantities. We analyze the convergence of the neural network solution of the VPFP system to that of the PNP system via the Asymptotic-Preserving (AP) scheme. Also, we provide several theoretical evidence that the Deep Neural Network (DNN) solutions to the VPFP and the PNP systems converge to the a priori classical solutions of each system if the total loss function vanishes.

Trend to Equilibrium for the Kinetic Fokker-Planck Equation via the Neural Network Approach

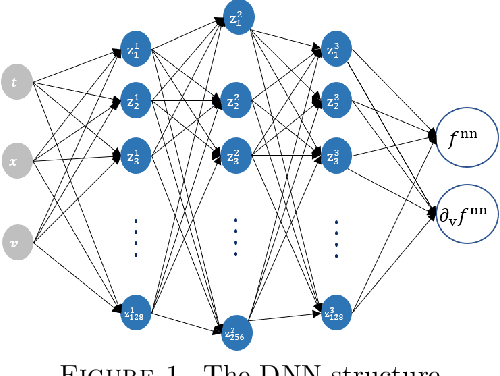
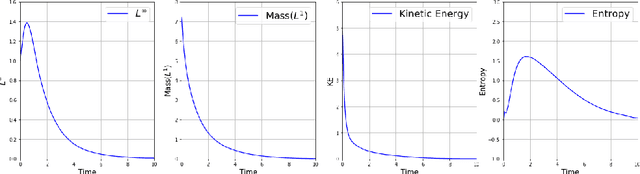
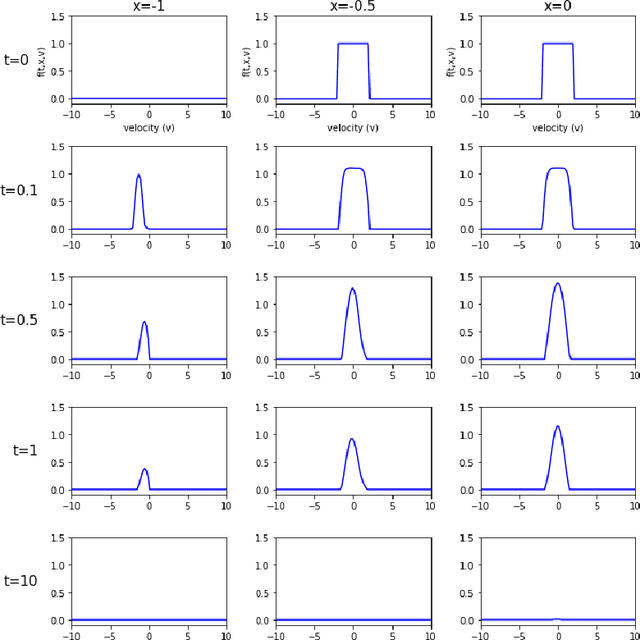
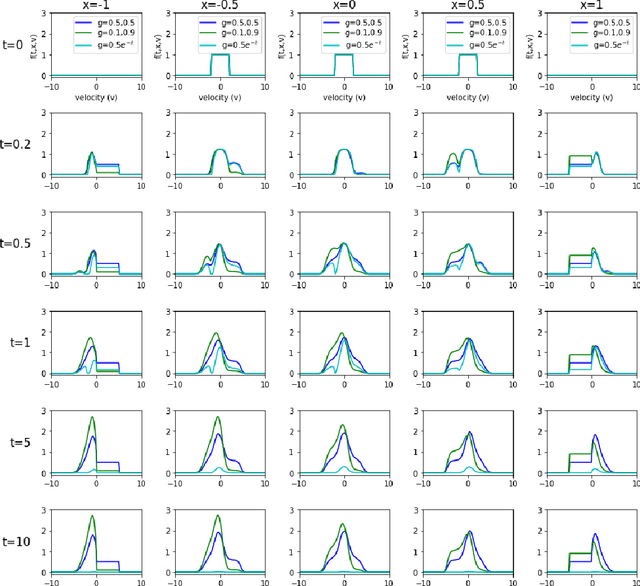
The issue of the relaxation to equilibrium has been at the core of the kinetic theory of rarefied gas dynamics. In the paper, we introduce the Deep Neural Network (DNN) approximated solutions to the kinetic Fokker-Planck equation in a bounded interval and study the large-time asymptotic behavior of the solutions and other physically relevant macroscopic quantities. We impose the varied types of boundary conditions including the inflow-type and the reflection-type boundaries as well as the varied diffusion and friction coefficients and study the boundary effects on the asymptotic behaviors. These include the predictions on the large-time behaviors of the pointwise values of the particle distribution and the macroscopic physical quantities including the total kinetic energy, the entropy, and the free energy. We also provide the theoretical supports for the pointwise convergence of the neural network solutions to the \textit{a priori} analytic solutions. We use the library \textit{PyTorch}, the activation function \textit{tanh} between layers, and the \textit{Adam} optimizer for the Deep Learning algorithm.