Trend to Equilibrium for the Kinetic Fokker-Planck Equation via the Neural Network Approach
Paper and Code
Nov 22, 2019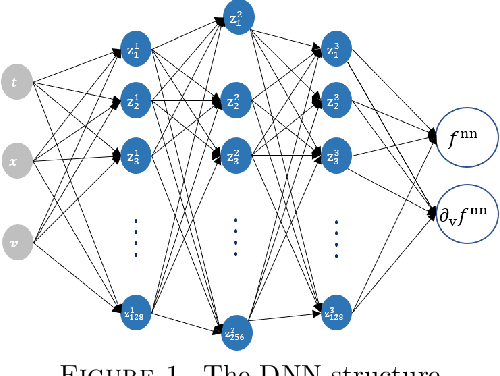
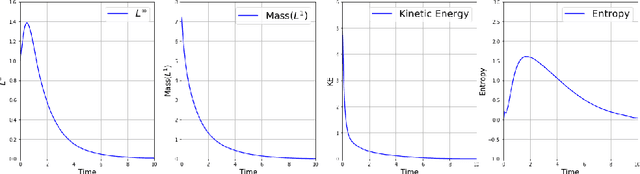
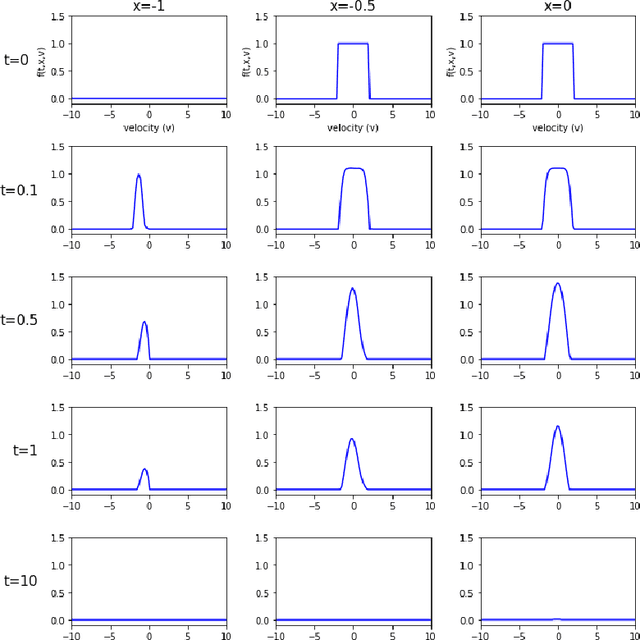
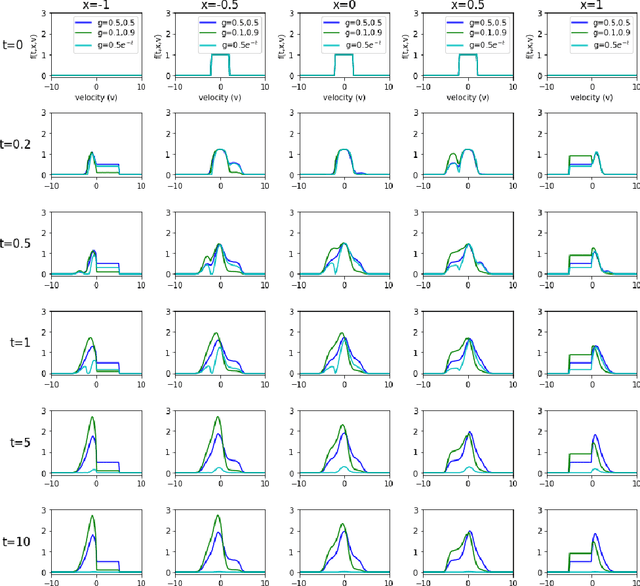
The issue of the relaxation to equilibrium has been at the core of the kinetic theory of rarefied gas dynamics. In the paper, we introduce the Deep Neural Network (DNN) approximated solutions to the kinetic Fokker-Planck equation in a bounded interval and study the large-time asymptotic behavior of the solutions and other physically relevant macroscopic quantities. We impose the varied types of boundary conditions including the inflow-type and the reflection-type boundaries as well as the varied diffusion and friction coefficients and study the boundary effects on the asymptotic behaviors. These include the predictions on the large-time behaviors of the pointwise values of the particle distribution and the macroscopic physical quantities including the total kinetic energy, the entropy, and the free energy. We also provide the theoretical supports for the pointwise convergence of the neural network solutions to the \textit{a priori} analytic solutions. We use the library \textit{PyTorch}, the activation function \textit{tanh} between layers, and the \textit{Adam} optimizer for the Deep Learning algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge