Physics-Informed Neural Networks for Optimal Vaccination Plan in SIR Epidemic Models

This work focuses on understanding the minimum eradication time for the controlled Susceptible-Infectious-Recovered (SIR) model in the time-homogeneous setting, where the infection and recovery rates are constant. The eradication time is defined as the earliest time the infectious population drops below a given threshold and remains below it. For time-homogeneous models, the eradication time is well-defined due to the predictable dynamics of the infectious population, and optimal control strategies can be systematically studied. We utilize Physics-Informed Neural Networks (PINNs) to solve the partial differential equation (PDE) governing the eradication time and derive the corresponding optimal vaccination control. The PINN framework enables a mesh-free solution to the PDE by embedding the dynamics directly into the loss function of a deep neural network. We use a variable scaling method to ensure stable training of PINN and mathematically analyze that this method is effective in our setting. This approach provides an efficient computational alternative to traditional numerical methods, allowing for an approximation of the eradication time and the optimal control strategy. Through numerical experiments, we validate the effectiveness of the proposed method in computing the minimum eradication time and achieving optimal control. This work offers a novel application of PINNs to epidemic modeling, bridging mathematical theory and computational practice for time-homogeneous SIR models.

Stochastic-Constrained Stochastic Optimization with Markovian Data

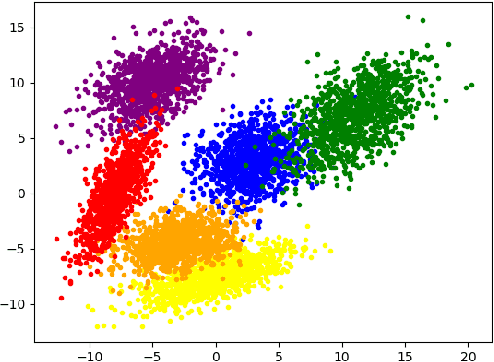
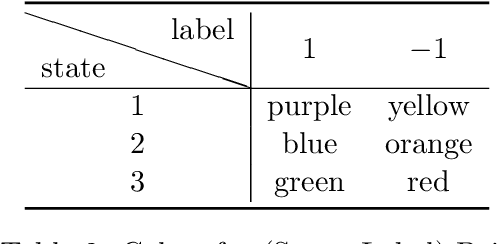
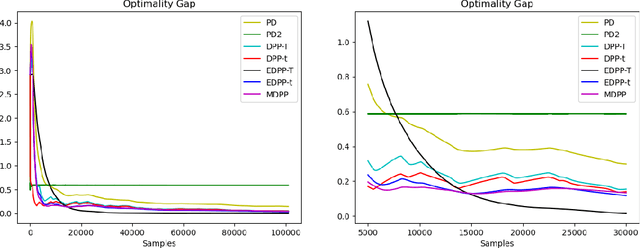
This paper considers stochastic-constrained stochastic optimization where the stochastic constraint is to satisfy that the expectation of a random function is below a certain threshold. In particular, we study the setting where data samples are drawn from a Markov chain and thus are not independent and identically distributed. We generalize the drift-plus-penalty framework, a primal-dual stochastic gradient method developed for the i.i.d. case, to the Markov chain sampling setting. We propose two variants of drift-plus-penalty; one is for the case when the mixing time of the underlying Markov chain is known while the other is for the case of unknown mixing time. In fact, our algorithms apply to a more general setting of constrained online convex optimization where the sequence of constraint functions follows a Markov chain. Both algorithms are adaptive in that the first works without knowledge of the time horizon while the second uses AdaGrad-style algorithm parameters, which is of independent interest. We demonstrate the effectiveness of our proposed methods through numerical experiments on classification with fairness constraints.

Online Convex Optimization with Stochastic Constraints: Zero Constraint Violation and Bandit Feedback

This paper studies online convex optimization with stochastic constraints. We propose a variant of the drift-plus-penalty algorithm that guarantees $O(\sqrt{T})$ expected regret and zero constraint violation, after a fixed number of iterations, which improves the vanilla drift-plus-penalty method with $O(\sqrt{T})$ constraint violation. Our algorithm is oblivious to the length of the time horizon $T$, in contrast to the vanilla drift-plus-penalty method. This is based on our novel drift lemma that provides time-varying bounds on the virtual queue drift and, as a result, leads to time-varying bounds on the expected virtual queue length. Moreover, we extend our framework to stochastic-constrained online convex optimization under two-point bandit feedback. We show that by adapting our algorithmic framework to the bandit feedback setting, we may still achieve $O(\sqrt{T})$ expected regret and zero constraint violation, improving upon the previous work for the case of identical constraint functions. Numerical results demonstrate our theoretical results.