Stochastic-Constrained Stochastic Optimization with Markovian Data
Paper and Code
Dec 07, 2023
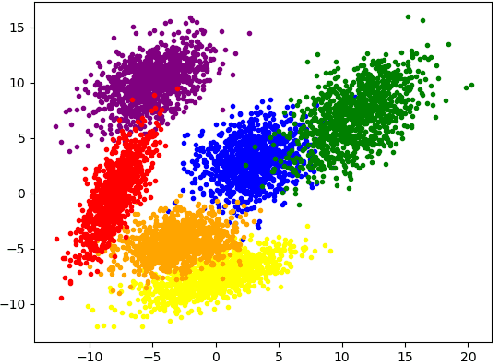
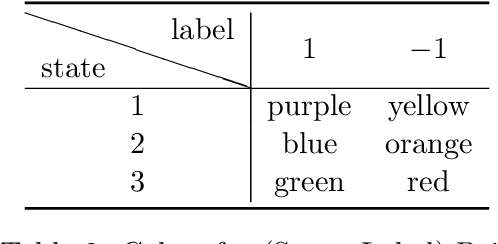
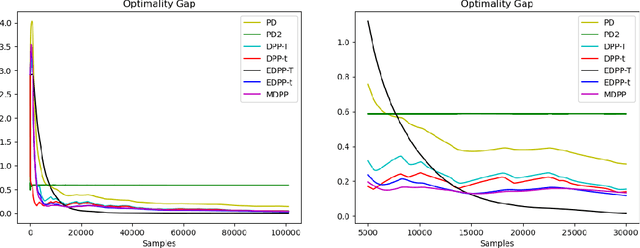
This paper considers stochastic-constrained stochastic optimization where the stochastic constraint is to satisfy that the expectation of a random function is below a certain threshold. In particular, we study the setting where data samples are drawn from a Markov chain and thus are not independent and identically distributed. We generalize the drift-plus-penalty framework, a primal-dual stochastic gradient method developed for the i.i.d. case, to the Markov chain sampling setting. We propose two variants of drift-plus-penalty; one is for the case when the mixing time of the underlying Markov chain is known while the other is for the case of unknown mixing time. In fact, our algorithms apply to a more general setting of constrained online convex optimization where the sequence of constraint functions follows a Markov chain. Both algorithms are adaptive in that the first works without knowledge of the time horizon while the second uses AdaGrad-style algorithm parameters, which is of independent interest. We demonstrate the effectiveness of our proposed methods through numerical experiments on classification with fairness constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge