Learning PDE Solution Operator for Continuous Modeling of Time-Series

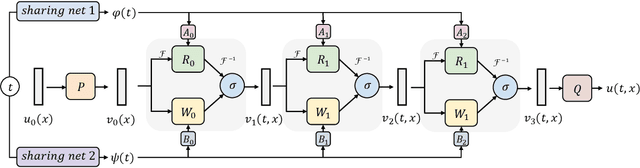
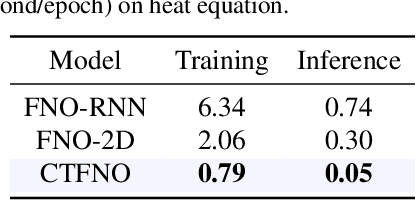
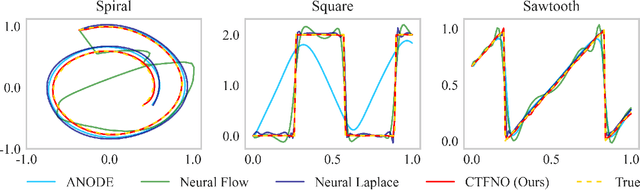
Learning underlying dynamics from data is important and challenging in many real-world scenarios. Incorporating differential equations (DEs) to design continuous networks has drawn much attention recently, however, most prior works make specific assumptions on the type of DEs, making the model specialized for particular problems. This work presents a partial differential equation (PDE) based framework which improves the dynamics modeling capability. Building upon the recent Fourier neural operator, we propose a neural operator that can handle time continuously without requiring iterative operations or specific grids of temporal discretization. A theoretical result demonstrating its universality is provided. We also uncover an intrinsic property of neural operators that improves data efficiency and model generalization by ensuring stability. Our model achieves superior accuracy in dealing with time-dependent PDEs compared to existing models. Furthermore, several numerical pieces of evidence validate that our method better represents a wide range of dynamics and outperforms state-of-the-art DE-based models in real-time-series applications. Our framework opens up a new way for a continuous representation of neural networks that can be readily adopted for real-world applications.

Robust Out-of-Distribution Detection on Deep Probabilistic Generative Models

Out-of-distribution (OOD) detection is an important task in machine learning systems for ensuring their reliability and safety. Deep probabilistic generative models facilitate OOD detection by estimating the likelihood of a data sample. However, such models frequently assign a suspiciously high likelihood to a specific outlier. Several recent works have addressed this issue by training a neural network with auxiliary outliers, which are generated by perturbing the input data. In this paper, we discover that these approaches fail for certain OOD datasets. Thus, we suggest a new detection metric that operates without outlier exposure. We observe that our metric is robust to diverse variations of an image compared to the previous outlier-exposing methods. Furthermore, our proposed score requires neither auxiliary models nor additional training. Instead, this paper utilizes the likelihood ratio statistic in a new perspective to extract genuine properties from the given single deep probabilistic generative model. We also apply a novel numerical approximation to enable fast implementation. Finally, we demonstrate comprehensive experiments on various probabilistic generative models and show that our method achieves state-of-the-art performance.

Do Not Escape From the Manifold: Discovering the Local Coordinates on the Latent Space of GANs

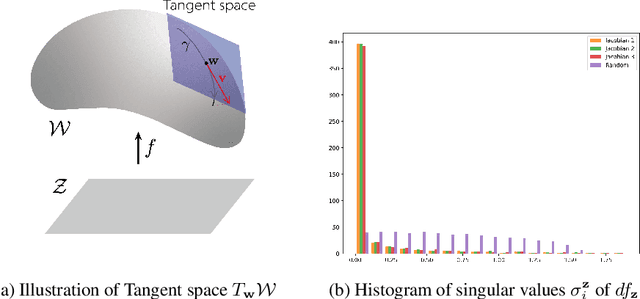
In this paper, we propose a method to find local-geometry-aware traversal directions on the intermediate latent space of Generative Adversarial Networks (GANs). These directions are defined as an ordered basis of tangent space at a latent code. Motivated by the intrinsic sparsity of the latent space, the basis is discovered by solving the low-rank approximation problem of the differential of the partial network. Moreover, the local traversal basis leads to a natural iterative traversal on the latent space. Iterative Curve-Traversal shows stable traversal on images, since the trajectory of latent code stays close to the latent space even under the strong perturbations compared to the linear traversal. This stability provides far more diverse variations of the given image. Although the proposed method can be applied to various GAN models, we focus on the W-space of the StyleGAN2, which is renowned for showing the better disentanglement of the latent factors of variation. Our quantitative and qualitative analysis provides evidence showing that the W-space is still globally warped while showing a certain degree of global consistency of interpretable variation. In particular, we introduce some metrics on the Grassmannian manifolds to quantify the global warpage of the W-space and the subspace traversal to test the stability of traversal directions.