Multivariate Quantile Function Forecaster

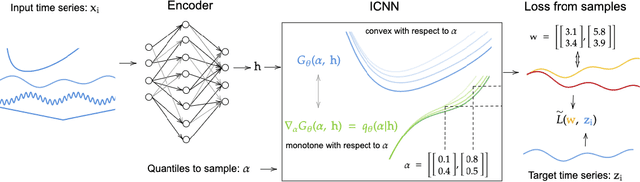
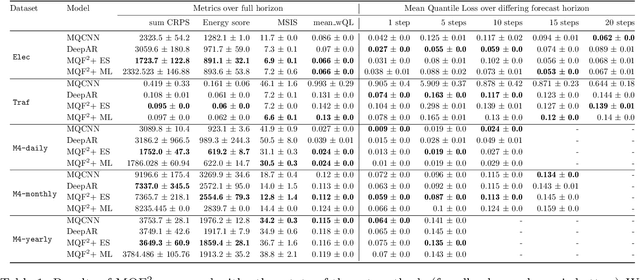
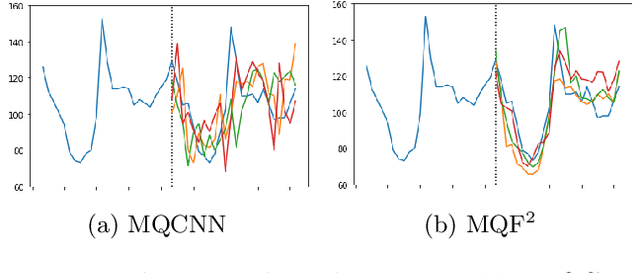
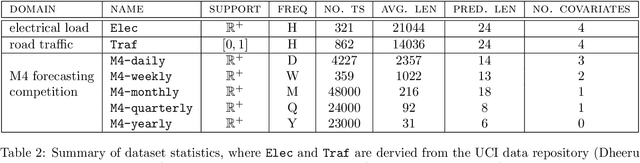
We propose Multivariate Quantile Function Forecaster (MQF$^2$), a global probabilistic forecasting method constructed using a multivariate quantile function and investigate its application to multi-horizon forecasting. Prior approaches are either autoregressive, implicitly capturing the dependency structure across time but exhibiting error accumulation with increasing forecast horizons, or multi-horizon sequence-to-sequence models, which do not exhibit error accumulation, but also do typically not model the dependency structure across time steps. MQF$^2$ combines the benefits of both approaches, by directly making predictions in the form of a multivariate quantile function, defined as the gradient of a convex function which we parametrize using input-convex neural networks. By design, the quantile function is monotone with respect to the input quantile levels and hence avoids quantile crossing. We provide two options to train MQF$^2$: with energy score or with maximum likelihood. Experimental results on real-world and synthetic datasets show that our model has comparable performance with state-of-the-art methods in terms of single time step metrics while capturing the time dependency structure.

Learning Quantile Functions without Quantile Crossing for Distribution-free Time Series Forecasting

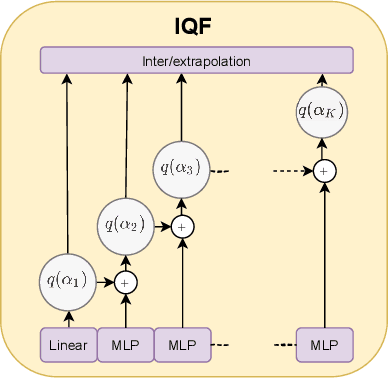
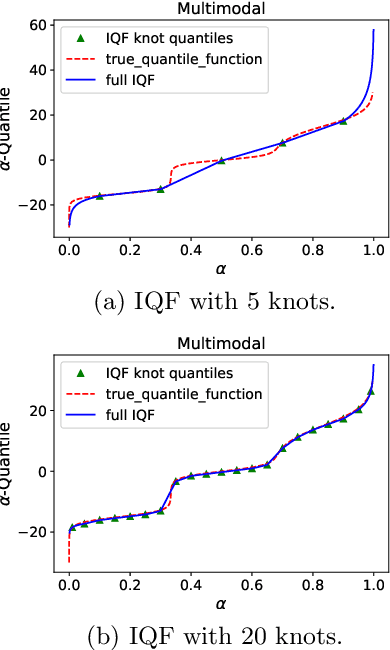
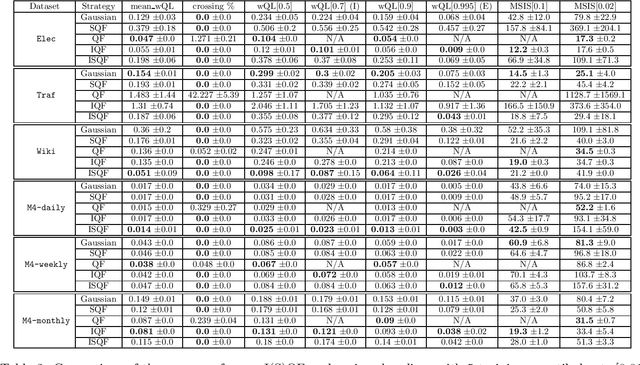
Quantile regression is an effective technique to quantify uncertainty, fit challenging underlying distributions, and often provide full probabilistic predictions through joint learnings over multiple quantile levels. A common drawback of these joint quantile regressions, however, is \textit{quantile crossing}, which violates the desirable monotone property of the conditional quantile function. In this work, we propose the Incremental (Spline) Quantile Functions I(S)QF, a flexible and efficient distribution-free quantile estimation framework that resolves quantile crossing with a simple neural network layer. Moreover, I(S)QF inter/extrapolate to predict arbitrary quantile levels that differ from the underlying training ones. Equipped with the analytical evaluation of the continuous ranked probability score of I(S)QF representations, we apply our methods to NN-based times series forecasting cases, where the savings of the expensive re-training costs for non-trained quantile levels is particularly significant. We also provide a generalization error analysis of our proposed approaches under the sequence-to-sequence setting. Lastly, extensive experiments demonstrate the improvement of consistency and accuracy errors over other baselines.

Avoiding The Double Descent Phenomenon of Random Feature Models Using Hybrid Regularization

We demonstrate the ability of hybrid regularization methods to automatically avoid the double descent phenomenon arising in the training of random feature models (RFM). The hallmark feature of the double descent phenomenon is a spike in the regularization gap at the interpolation threshold, i.e. when the number of features in the RFM equals the number of training samples. To close this gap, the hybrid method considered in our paper combines the respective strengths of the two most common forms of regularization: early stopping and weight decay. The scheme does not require hyperparameter tuning as it automatically selects the stopping iteration and weight decay hyperparameter by using generalized cross-validation (GCV). This also avoids the necessity of a dedicated validation set. While the benefits of hybrid methods have been well-documented for ill-posed inverse problems, our work presents the first use case in machine learning. To expose the need for regularization and motivate hybrid methods, we perform detailed numerical experiments inspired by image classification. In those examples, the hybrid scheme successfully avoids the double descent phenomenon and yields RFMs whose generalization is comparable with classical regularization approaches whose hyperparameters are tuned optimally using the test data. We provide our MATLAB codes for implementing the numerical experiments in this paper at https://github.com/EmoryMLIP/HybridRFM.