Non-linear Independent Dual System (NIDS) for Discretization-independent Surrogate Modeling over Complex Geometries

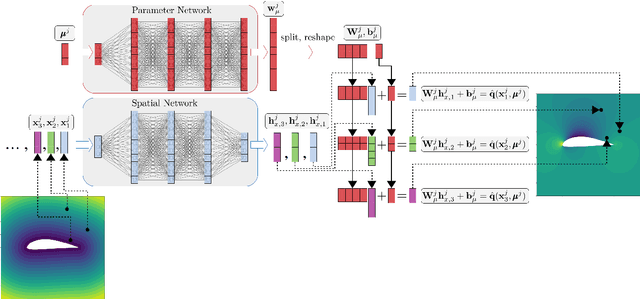
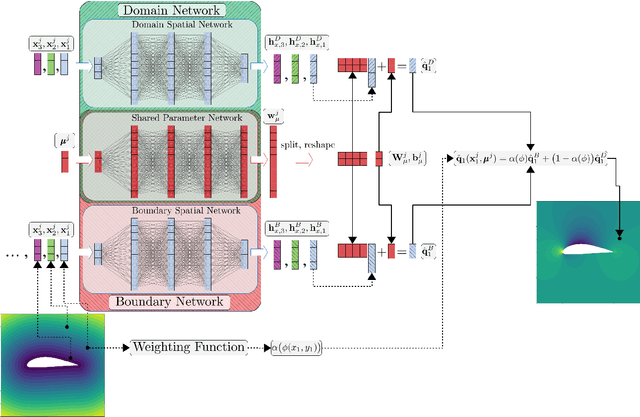
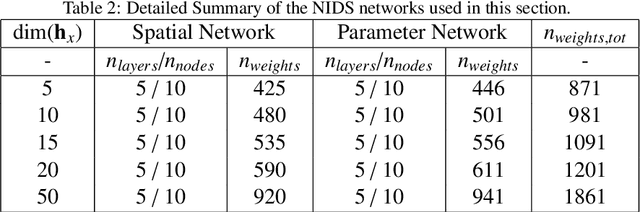
Numerical solutions of partial differential equations (PDEs) require expensive simulations, limiting their application in design optimization routines, model-based control, or solution of large-scale inverse problems. Existing Convolutional Neural Network-based frameworks for surrogate modeling require lossy pixelization and data-preprocessing, which is not suitable for realistic engineering applications. Therefore, we propose non-linear independent dual system (NIDS), which is a deep learning surrogate model for discretization-independent, continuous representation of PDE solutions, and can be used for prediction over domains with complex, variable geometries and mesh topologies. NIDS leverages implicit neural representations to develop a non-linear mapping between problem parameters and spatial coordinates to state predictions by combining evaluations of a case-wise parameter network and a point-wise spatial network in a linear output layer. The input features of the spatial network include physical coordinates augmented by a minimum distance function evaluation to implicitly encode the problem geometry. The form of the overall output layer induces a dual system, where each term in the map is non-linear and independent. Further, we propose a minimum distance function-driven weighted sum of NIDS models using a shared parameter network to enforce boundary conditions by construction under certain restrictions. The framework is applied to predict solutions around complex, parametrically-defined geometries on non-parametrically-defined meshes with solutions obtained many orders of magnitude faster than the full order models. Test cases include a vehicle aerodynamics problem with complex geometry and data scarcity, enabled by a training method in which more cases are gradually added as training progresses.