Spatially-Aware Diffusion Models with Cross-Attention for Global Field Reconstruction with Sparse Observations

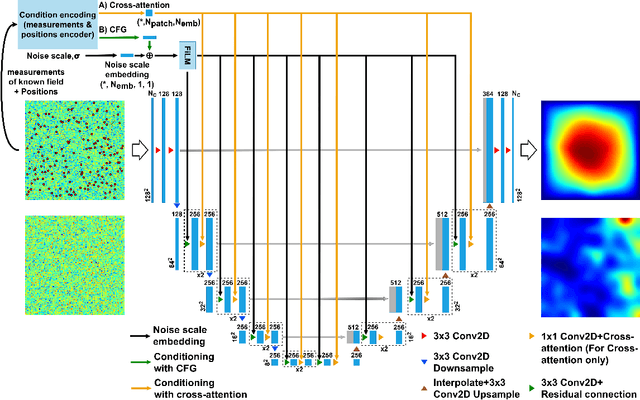
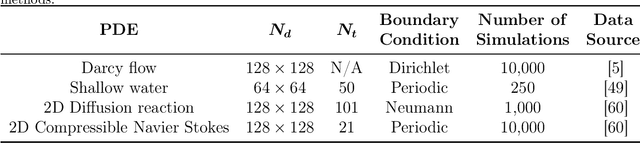
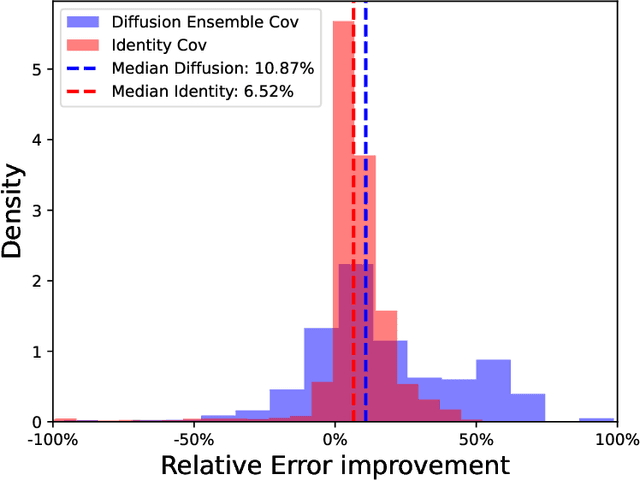
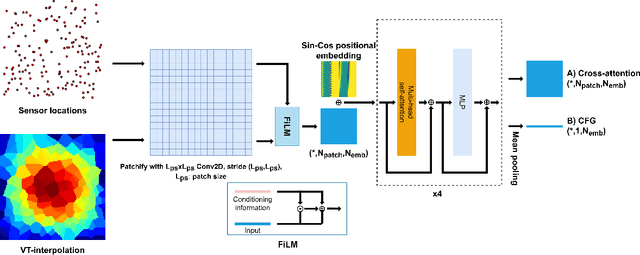
Diffusion models have gained attention for their ability to represent complex distributions and incorporate uncertainty, making them ideal for robust predictions in the presence of noisy or incomplete data. In this study, we develop and enhance score-based diffusion models in field reconstruction tasks, where the goal is to estimate complete spatial fields from partial observations. We introduce a condition encoding approach to construct a tractable mapping mapping between observed and unobserved regions using a learnable integration of sparse observations and interpolated fields as an inductive bias. With refined sensing representations and an unraveled temporal dimension, our method can handle arbitrary moving sensors and effectively reconstruct fields. Furthermore, we conduct a comprehensive benchmark of our approach against a deterministic interpolation-based method across various static and time-dependent PDEs. Our study attempts to addresses the gap in strong baselines for evaluating performance across varying sampling hyperparameters, noise levels, and conditioning methods. Our results show that diffusion models with cross-attention and the proposed conditional encoding generally outperform other methods under noisy conditions, although the deterministic method excels with noiseless data. Additionally, both the diffusion models and the deterministic method surpass the numerical approach in accuracy and computational cost for the steady problem. We also demonstrate the ability of the model to capture possible reconstructions and improve the accuracy of fused results in covariance-based correction tasks using ensemble sampling.

CoCoGen: Physically-Consistent and Conditioned Score-based Generative Models for Forward and Inverse Problems

Recent advances in generative artificial intelligence have had a significant impact on diverse domains spanning computer vision, natural language processing, and drug discovery. This work extends the reach of generative models into physical problem domains, particularly addressing the efficient enforcement of physical laws and conditioning for forward and inverse problems involving partial differential equations (PDEs). Our work introduces two key contributions: firstly, we present an efficient approach to promote consistency with the underlying PDE. By incorporating discretized information into score-based generative models, our method generates samples closely aligned with the true data distribution, showcasing residuals comparable to data generated through conventional PDE solvers, significantly enhancing fidelity. Secondly, we showcase the potential and versatility of score-based generative models in various physics tasks, specifically highlighting surrogate modeling as well as probabilistic field reconstruction and inversion from sparse measurements. A robust foundation is laid by designing unconditional score-based generative models that utilize reversible probability flow ordinary differential equations. Leveraging conditional models that require minimal training, we illustrate their flexibility when combined with a frozen unconditional model. These conditional models generate PDE solutions by incorporating parameters, macroscopic quantities, or partial field measurements as guidance. The results illustrate the inherent flexibility of score-based generative models and explore the synergy between unconditional score-based generative models and the present physically-consistent sampling approach, emphasizing the power and flexibility in solving for and inverting physical fields governed by differential equations, and in other scientific machine learning tasks.

Semi-supervised Variational Autoencoder for Regression: Application on Soft Sensors

We present the development of a semi-supervised regression method using variational autoencoders (VAE), which is customized for use in soft sensing applications. We motivate the use of semi-supervised learning considering the fact that process quality variables are not collected at the same frequency as other process variables leading to many unlabelled records in operational datasets. These unlabelled records are not possible to use for training quality variable predictions based on supervised learning methods. Use of VAEs for unsupervised learning is well established and recently they were used for regression applications based on variational inference procedures. We extend this approach of supervised VAEs for regression (SVAER) to make it learn from unlabelled data leading to semi-supervised VAEs for regression (SSVAER), then we make further modifications to their architecture using additional regularization components to make SSVAER well suited for learning from both labelled and unlabelled process data. The probabilistic regressor resulting from the variational approach makes it possible to estimate the variance of the predictions simultaneously, which provides an uncertainty quantification along with the generated predictions. We provide an extensive comparative study of SSVAER with other publicly available semi-supervised and supervised learning methods on two benchmark problems using fixed-size datasets, where we vary the percentage of labelled data available for training. In these experiments, SSVAER achieves the lowest test errors in 11 of the 20 studied cases, compared to other methods where the second best gets 4 lowest test errors out of the 20.