Spatially-Aware Diffusion Models with Cross-Attention for Global Field Reconstruction with Sparse Observations
Paper and Code
Aug 30, 2024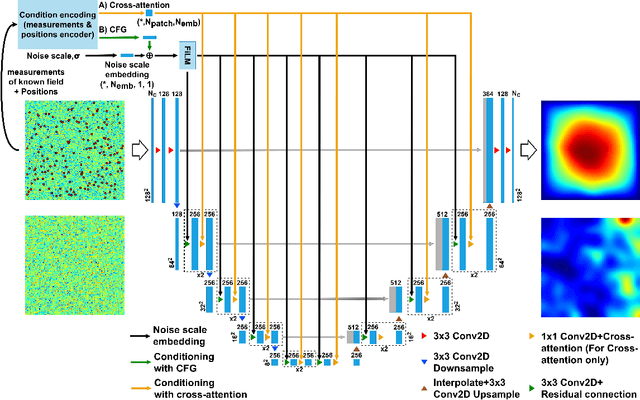
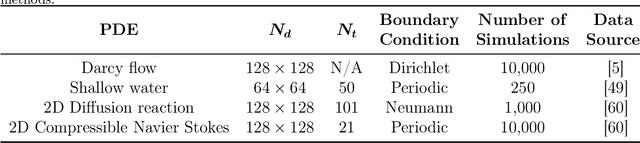
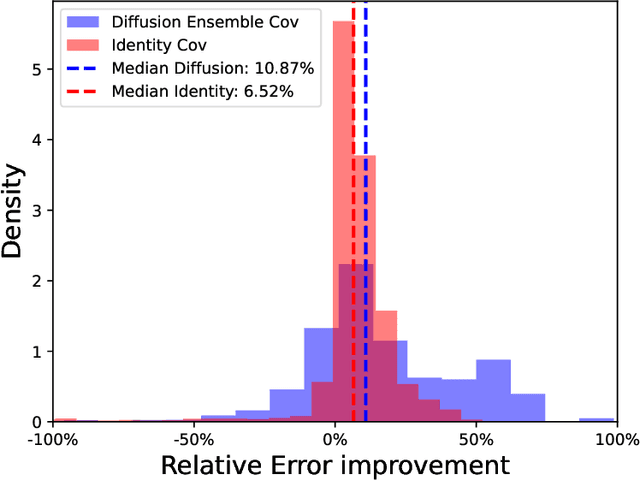
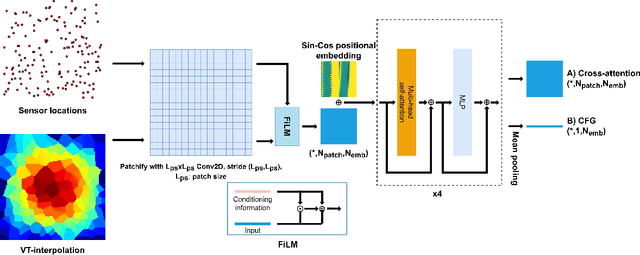
Diffusion models have gained attention for their ability to represent complex distributions and incorporate uncertainty, making them ideal for robust predictions in the presence of noisy or incomplete data. In this study, we develop and enhance score-based diffusion models in field reconstruction tasks, where the goal is to estimate complete spatial fields from partial observations. We introduce a condition encoding approach to construct a tractable mapping mapping between observed and unobserved regions using a learnable integration of sparse observations and interpolated fields as an inductive bias. With refined sensing representations and an unraveled temporal dimension, our method can handle arbitrary moving sensors and effectively reconstruct fields. Furthermore, we conduct a comprehensive benchmark of our approach against a deterministic interpolation-based method across various static and time-dependent PDEs. Our study attempts to addresses the gap in strong baselines for evaluating performance across varying sampling hyperparameters, noise levels, and conditioning methods. Our results show that diffusion models with cross-attention and the proposed conditional encoding generally outperform other methods under noisy conditions, although the deterministic method excels with noiseless data. Additionally, both the diffusion models and the deterministic method surpass the numerical approach in accuracy and computational cost for the steady problem. We also demonstrate the ability of the model to capture possible reconstructions and improve the accuracy of fused results in covariance-based correction tasks using ensemble sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge